Углы в треугольниках играют важную роль в геометрии, а их измерение в градусах помогает нам понять и представить форму и размеры фигуры. Но как найти угол треугольника? Это вопрос, с которым сталкиваются не только ученики и студенты, но и все, кто интересуется математикой и геометрией.
Для нахождения угла треугольника необходимо знать известные данные о фигуре, используя которые можно применить различные формулы и методы. Существуют несколько способов нахождения углов треугольника, но самые распространенные включают использование теоремы синусов, теоремы косинусов, а также знания о сумме углов треугольника.
Одним из способов нахождения угла треугольника является применение теоремы синусов. Согласно этой теореме, отношение длины стороны треугольника к синусу ее противолежащего угла равно постоянному значению. Используя эту формулу и известные данные о двух сторонах и угле, можно вычислить третий угол треугольника.
Теорема косинусов является также одним из методов нахождения угла треугольника. Она устанавливает связь между сторонами треугольника и косинусами его углов. При помощи этой теоремы можно вычислить угол, зная длины всех трех сторон треугольника.
Угол треугольника: определение и значение
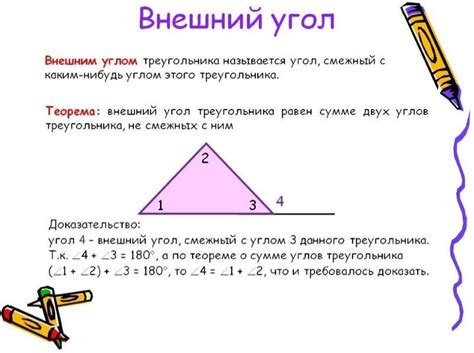
Значение угла треугольника определяется его мерой, которая измеряется в градусах. Градус – это единица измерения для углов, которая равна 1/360 окружности. Таким образом, полный угол – это 360 градусов.
В треугольнике существуют три основных типа углов:
- Острый угол: угол, мера которого меньше 90 градусов.
- Прямой угол: угол, мера которого равна 90 градусам. Прямой угол обычно обозначается вертикальной линией в угловой точке.
- Тупой угол: угол, мера которого больше 90 градусов, но меньше 180 градусов.
В треугольнике сумма мер всех углов всегда равна 180 градусов. Это свойство называется суммой углов треугольника.
Зная значения двух углов треугольника, можно вычислить третий угол, вычитая сумму мер из 180 градусов. Например, если два угла треугольника равны 30 градусов и 60 градусов, то третий угол будет равен 180 - 30 - 60 = 90 градусов.
Зная значения всех трех углов треугольника, можно судить о его форме:
- Равносторонний треугольник: все три угла равны между собой и равны 60 градусам.
- Равнобедренный треугольник: два угла равны между собой.
- Разносторонний треугольник: все три угла различны и не равны 180 градусам.
Определение и значение угла треугольника являются основными элементами для изучения геометрии треугольников и их свойств.
Способы нахождения угла треугольника в градусах

Для нахождения угла треугольника в градусах можно использовать несколько способов. Они основаны на различных свойствах и формулах треугольников, а также на знании значений других углов или сторон.
1. Использование тригонометрических функций
Для нахождения угла треугольника в градусах с использованием тригонометрических функций можно воспользоваться формулами синуса, косинуса или тангенса. Например, если известны значения двух сторон треугольника и угла между ними, можно использовать формулу косинуса:
| Формула косинуса | Применение |
|---|---|
| cos(A) = (b^2 + c^2 - a^2) / (2 * b * c) | Нахождение угла A |
| cos(B) = (a^2 + c^2 - b^2) / (2 * a * c) | Нахождение угла B |
| cos(C) = (a^2 + b^2 - c^2) / (2 * a * b) | Нахождение угла C |
2. Использование теоремы косинусов
Теорема косинусов позволяет находить углы треугольника в градусах по длинам его сторон. Если известны значения всех трех сторон треугольника, то можно использовать формулу теоремы косинусов:
| Формула теоремы косинусов | Применение |
|---|---|
| cos(A) = (b^2 + c^2 - a^2) / (2 * b * c) | Нахождение угла A |
| cos(B) = (a^2 + c^2 - b^2) / (2 * a * c) | Нахождение угла B |
| cos(C) = (a^2 + b^2 - c^2) / (2 * a * b) | Нахождение угла C |
3. Использование теоремы синусов
Теорема синусов также позволяет находить углы треугольника в градусах по длинам его сторон. Если известны значения всех трех сторон треугольника, то можно использовать формулу теоремы синусов:
| Формула теоремы синусов | Применение |
|---|---|
| sin(A) = (a / c) | Нахождение угла A |
| sin(B) = (b / c) | Нахождение угла B |
| sin(C) = (a / b) | Нахождение угла C |
Теперь вы знаете несколько способов нахождения угла треугольника в градусах. Используя эти формулы и свойства треугольников, вы сможете с легкостью решать задачи, связанные с нахождением углов треугольников.
Использование тригонометрии для определения угла треугольника
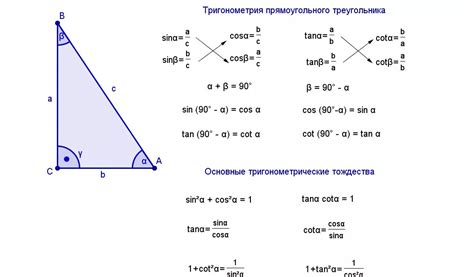
Для определения угла треугольника с использованием тригонометрии, нам понадобятся значения сторон треугольника и соответствующих им углов.
Существует несколько тригонометрических функций, которые помогут нам вычислить углы треугольника: синус (sin), косинус (cos) и тангенс (tan).
Синус (sin) угла треугольника определяется отношением противолежащей стороны к гипотенузе. Формула для расчета синуса угла выглядит следующим образом:
sin(A) = противолежащая сторона / гипотенуза
Косинус (cos) угла треугольника определяется отношением прилежащей стороны к гипотенузе. Формула для расчета косинуса угла выглядит следующим образом:
cos(A) = прилежащая сторона / гипотенуза
Тангенс (tan) угла треугольника определяется отношением противолежащей стороны к прилежащей стороне. Формула для расчета тангенса угла выглядит следующим образом:
tan(A) = противолежащая сторона / прилежащая сторона
После того, как мы найдем значение функции, мы можем использовать обратные тригонометрические функции (например, arcsin, arccos, arctan) для определения угла треугольника.
Например, если мы знаем значения противолежащей стороны и гипотенузы треугольника, мы можем использовать sin-1 для определения угла:
A = sin-1(противолежащая сторона / гипотенуза)
Аналогично, можно использовать cos-1 или tan-1 для определения углов треугольника с использованием других соотношений сторон.
Таким образом, тригонометрия позволяет нам вычислять углы треугольника с использованием известных значений сторон и соответствующих тригонометрических функций.
Использование геометрических формул для определения угла треугольника
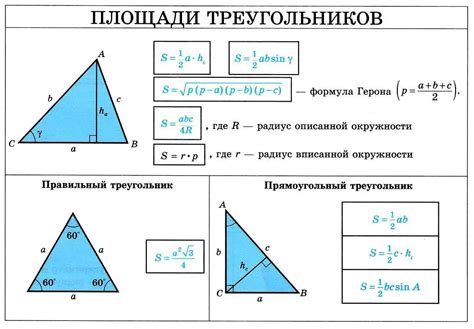
Одной из самых простых формул для определения угла треугольника является геометрическое правило, известное как "Сумма углов треугольника". Согласно этому правилу, сумма трех углов треугольника всегда равна 180 градусам. Таким образом, если у нас есть значения двух углов, мы можем легко определить значение третьего угла. Например, если угол А равен 60 градусам, а угол В равен 40 градусам, то угол С можно определить, вычтя сумму углов А и В (60 + 40 = 100 градусов) из 180 градусов.
Другая формула, которая также позволяет определить угол треугольника, - это теорема синусов. Согласно этой теореме, отношение синуса угла треугольника к длине противоположной ему стороны является постоянной величиной для данного треугольника. Таким образом, если нам известны длины двух сторон и соответствующий им угол треугольника, мы можем использовать формулу синусов для нахождения значения третьего угла. Например, при известных значениях a = 5, b = 7 и угле A = 30 градусов, мы можем использовать формулу синусов sin(C) = c / a, где c - это значение третьей стороны треугольника. Решая эту формулу, мы получаем значения всех трех углов.
Геометрические формулы для определения углов треугольников позволяют нам находить значения углов, основываясь на известных данных о треугольнике. Они играют важную роль в геометрии и используются для решения многочисленных задач.
Примеры решения задач на нахождение угла треугольника в градусах

Для решения задач на нахождение угла треугольника в градусах необходимо использовать различные методы и формулы. Вот несколько примеров таких задач:
Пример 1:
Дан треугольник ABC, где AB = 5 см, BC = 7 см и AC = 8 см. Найдите угол BAC в градусах.
| Шаг | Действие | Пояснение |
|---|---|---|
| 1 | Найдите наибольшую сторону треугольника | В данном случае наибольшая сторона - AC (8 см) |
| 2 | Используйте закон косинусов для нахождения угла BAC | cos(BAC) = (AB^2 + AC^2 - BC^2) / (2 * AB * AC) |
| 3 | Подставьте значения сторон в формулу | cos(BAC) = (5^2 + 8^2 - 7^2) / (2 * 5 * 8) = 64 / 80 = 0.8 |
| 4 | Используйте обратную функцию косинуса для нахождения угла BAC | BAC = arccos(0.8) ≈ 37.38° |
Пример 2:
Дан треугольник ABC, где AB = 10 см, BC = 12 см и угол BAC = 60°. Найдите угол ABC в градусах.
| Шаг | Действие | Пояснение |
|---|---|---|
| 1 | Используйте закон синусов для нахождения стороны AC | AC / sin(BAC) = BC / sin(ABC) |
| 2 | Подставьте значения сторон и угла в формулу | AC / sin(60°) = 12 / sin(ABC) |
| 3 | Решите уравнение и найдите AC | AC = (12 * sin(60°)) / sin(ABC) ≈ 13.85 см |
| 4 | Используйте закон косинусов для нахождения угла ABC | cos(ABC) = (AC^2 + BC^2 - AB^2) / (2 * AC * BC) |
| 5 | Подставьте значения сторон в формулу | cos(ABC) = (13.85^2 + 12^2 - 10^2) / (2 * 13.85 * 12) ≈ 0.7743 |
| 6 | Используйте обратную функцию косинуса для нахождения угла ABC | ABC = arccos(0.7743) ≈ 40.11° |
Это лишь два примера решения задач на нахождение угла треугольника в градусах. В каждой задаче может быть своя особенность и использоваться разные методы и формулы. Важно помнить основные законы треугольников и уметь применять их при решении подобных задач.