Нахождение угла вершины через стороны является одной из важных задач в геометрии. Это может пригодиться, например, при построении треугольника по заданным сторонам или при решении различных геометрических задач.
Для решения этой задачи можно использовать теорему косинусов, которая устанавливает связь между сторонами треугольника и его углами. Согласно теореме косинусов, квадрат стороны треугольника равен сумме квадратов двух других сторон, умноженной на два произведение этих сторон на косинус угла между ними.
Чтобы найти угол вершины через стороны, нужно начать с известных значений - длин сторон треугольника инициализируйте переменные a, b и c. Затем можно применить теорему косинусов, чтобы найти значение косинуса искомого угла. После этого, используя обратную функцию косинуса (arccos), можно найти сам угол вершины.
В этой подробной инструкции мы рассмотрим каждый шаг подробно и покажем примеры расчетов. Если вы хотите научиться находить угол вершины через стороны, то эта статья поможет вам разобраться в этом вопросе и освоить этот метод расчета.
Методика определения угла вершины через стороны

Чтобы найти угол вершины треугольника через стороны, можно использовать тригонометрические функции. Для этого необходимо знать длины двух сторон треугольника и градусную меру угла между этими сторонами.
Для начала, обозначим данную сторону треугольника, угол вершины которого мы хотим найти, как "с". Отметим длины других двух сторон как "а" и "b".
Используя теорему косинусов, можно записать следующее уравнение:
| с2 = а2 + b2 - 2*а*б*cos(C) |
Где "с" - искомая сторона, "а" и "b" - длины известных сторон, "С" - градусная мера угла между этими сторонами.
Далее, выразим градусную меру угла между сторонами "а" и "б" через длины сторон и искомый угол вершины:
| cos(C) = (а2 + b2 - c2) / (2*а*б) |
Наконец, с помощью тригонометрической функции обратного косинуса, находим градусную меру угла:
| C = arccos((а2 + b2 - c2) / (2*а*б)) |
Таким образом, используя данную методику, можно найти градусную меру угла вершины треугольника через известные стороны и градусный угол между ними.
Описание метода
Найдем угол вершины треугольника, если известны длины его сторон. Для этого воспользуемся теоремой косинусов. Теорема косинусов гласит:
В квадрате любой стороны треугольника равен сумме квадратов двух других сторон, умноженных на удельный косинус угла между ними.
Обозначим стороны треугольника как a, b и c, а углы противолежащие этим сторонам - A, B и C соответственно. Угол вершины треугольника обозначим как X.
Используя теорему косинусов, можно записать следующее:
a^2 = b^2 + c^2 - 2*b*c*cos(A)
Соответственно, угол X можно найти, применяя обратные функции косинуса:
X = arccos((b^2 + c^2 - a^2) / (2*b*c))
Таким образом, для нахождения угла вершины треугольника, необходимо воспользоваться формулой выше, подставив известные значения длин сторон треугольника.
Первый шаг: Измерение сторон треугольника
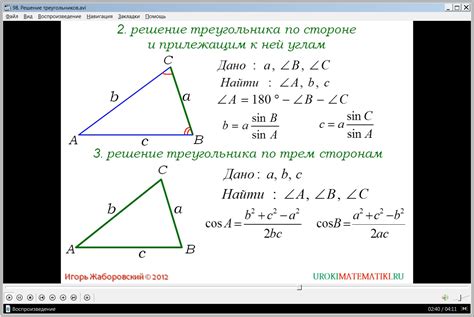
Прежде чем найти угол вершины треугольника, необходимо измерить длины его сторон. Для этого вам потребуется линейка или другой инструмент для измерения. Следуйте инструкциям ниже:
- Выберите одну из сторон треугольника и пометьте ее как AB.
- Разместите начало линейки в точке A и измерьте длину стороны AB.
- Запишите полученный результат.
- Повторите процесс для каждой из оставшихся сторон треугольника, помечая соответствующие стороны и измеряя их длину.
- Запишите длины всех сторон треугольника.
После того, как вы измерили все стороны треугольника и записали их длины, вы готовы перейти ко второму шагу - нахождению угла вершины.
Второй шаг: Применение теоремы косинусов

Для нахождения угла вершины треугольника по заданным длинам сторон можно использовать теорему косинусов.
Теорема косинусов позволяет связать длины сторон треугольника с косинусом угла между этими сторонами.
Формула теоремы косинусов имеет вид:
a2 = b2 + c2 - 2bc * cos(A)
где a - длина стороны треугольника противолежащей углу A, b и c - длины других двух сторон.
Для нахождения угла A мы можем переписать формулу:
cos(A) = (b2 + c2 - a2) / (2bc)
Теперь, зная длины сторон треугольника, мы можем подставить их в формулу и вычислить косинус угла A.
Затем, чтобы найти значение самого угла A, мы можем воспользоваться таблицей или калькулятором, которые выдают значение угла по его косинусу.
Применение теоремы косинусов позволяет точно находить угол вершины треугольника по заданным длинам его сторон.
Примеры решения

Рассмотрим несколько примеров, чтобы лучше понять, как найти угол вершины через стороны.
Пример 1:
Дан треугольник ABC, где сторона AB равна 5 см, сторона BC равна 8 см, а сторона AC равна 6 см. Найдём угол вершины B.
1. Используем теорему косинусов: c^2 = a^2 + b^2 - 2ab * cos(C), где c - сторона противолежащая углу, a и b - остальные две стороны, C - угол противолежащий стороне c.
2. Подставляем известные значения в формулу: 8^2 = 5^2 + 6^2 - 2 * 5 * 6 * cos(B).
3. Решаем уравнение для cos(B): 64 = 25 + 36 - 60 * cos(B).
4. Вычитаем из обеих частей уравнения 25 и 36: 3 = - 60 * cos(B).
5. Делим обе части уравнения на -60: cos(B) = -1/20.
6. Находим значение угла B, используя обратную функцию косинуса: B = arccos(-1/20).
7. Подсчитываем значение угла: B ≈ 93.135°.
Пример 2:
Дан треугольник XYZ, где сторона XY равна 10 см, сторона YZ равна 12 см, а сторона XZ равна 8 см. Найдём угол вершины X.
1. Используем теорему косинусов: c^2 = a^2 + b^2 - 2ab * cos(C), где c - сторона противолежащая углу, a и b - остальные две стороны, C - угол противолежащий стороне c.
2. Подставляем известные значения в формулу: 8^2 = 10^2 + 12^2 - 2 * 10 * 12 * cos(X).
3. Решаем уравнение для cos(X): 64 = 100 + 144 - 240 * cos(X).
4. Вычитаем из обеих частей уравнения 100 и 144: -180 = - 240 * cos(X).
5. Делим обе части уравнения на -240: cos(X) = -180/-240 = 3/4.
6. Находим значение угла X, используя обратную функцию косинуса: X = arccos(3/4).
7. Подсчитываем значение угла: X ≈ 41.41°.