Уравнение плоскости является одной из ключевых тем в линейной алгебре и важным инструментом в геометрии. Зная координаты трех точек, можно найти уравнение плоскости, проходящей через эти точки. Это уравнение позволяет описать положение плоскости в трехмерном пространстве и решить множество задач, связанных с геометрией и физикой.
Процесс нахождения уравнения плоскости через три точки может показаться сложным на первый взгляд, но на самом деле он довольно прост. Для начала, необходимо выбрать любые три точки, не лежащие на одной прямой. Затем, составляем систему уравнений, в которой каждое уравнение представляет собой условие, что плоскость проходит через каждую точку.
Решение этой системы уравнений приводит к нахождению коэффициентов уравнения плоскости. Полученное уравнение можно записать в виде Ax + By + Cz + D = 0, где A, B, C и D - это числа, выражающие коэффициенты плоскости, а x, y и z - переменные, выражающие координаты точек.
Как найти уравнение плоскости через три точки: примеры решения

Для начала, обозначим наши три точки как A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3). Чтобы найти уравнение плоскости, проходящей через эти точки, нам необходимо найти нормаль к плоскости.
Шаги для нахождения уравнения плоскости:
- Найдите векторы AB и AC, используя вычитание координат точек.
- Найдите векторное произведение векторов AB и AC. Векторное произведение даст нам нормаль к плоскости.
- Используйте полученные компоненты нормали и координаты одной из точек (например, A) для записи уравнения плоскости в виде Ax + By + Cz + D = 0.
Пример решения:
Пусть у нас есть три точки: A(1, 2, 3), B(4, 5, 6) и C(7, 8, 9).
Найдем векторы AB и AC:
AB = B - A = (4-1, 5-2, 6-3) = (3, 3, 3)
AC = C - A = (7-1, 8-2, 9-3) = (6, 6, 6)
Теперь найдем векторное произведение AB и AC:
N = AB x AC = (3, 3, 3) x (6, 6, 6) = (0, 18, -18)
Таким образом, нормаль к плоскости равна (0, 18, -18).
Используя координаты точки A(1, 2, 3) и компоненты нормали (0, 18, -18), мы можем записать уравнение плоскости:
0x + 18y - 18z + D = 0
Для нахождения D подставим координаты точки A:
0*1 + 18*2 - 18*3 + D = 0
36 - 54 + D = 0
D = 18
Итак, уравнение плоскости через точки A(1, 2, 3), B(4, 5, 6) и C(7, 8, 9) будет:
18y - 18z + 18 = 0
Метод Гаусса для нахождения уравнения плоскости

| x | y | z | 1 |
|---|---|---|---|
| x_1 | y_1 | z_1 | 1 |
| x_2 | y_2 | z_2 | 1 |
| x_3 | y_3 | z_3 | 1 |
Где (x_1, y_1, z_1), (x_2, y_2, z_2) и (x_3, y_3, z_3) – координаты трех точек, через которые требуется провести плоскость.
Шаги решения методом Гаусса:
- Запишите расширенную матрицу данной системы уравнений.
- Приведите расширенную матрицу к ступенчатому виду при помощи элементарных преобразований.
- Приведите расширенную матрицу к улучшенному ступенчатому виду при помощи элементарных преобразований.
- Запишите уравнение плоскости в виде a * x + b * y + c * z + d = 0 используя улучшенную ступенчатую матрицу.
- Выразите a, b, c и d.
Полученное уравнение плоскости вида a * x + b * y + c * z + d = 0 будет задавать плоскость, проходящую через три заданные точки (x_1, y_1, z_1), (x_2, y_2, z_2) и (x_3, y_3, z_3).
Метод Гаусса позволяет найти уравнение плоскости через три точки с высокой точностью и широко применяется в различных областях, требующих анализа трехмерных данных и построение моделей.
Метод использования векторного произведения для определения уравнения плоскости
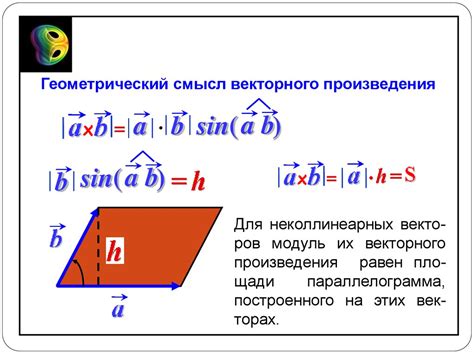
Для решения задачи найдем векторы, которые образуют две стороны треугольника, образованного этими точками. Затем применим свойство векторного произведения, которое позволяет определить нормальный вектор к плоскости.
Пусть даны три точки A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3).
Найдем вектора AB и AC следующим образом:
AB = (x2 - x1, y2 - y1, z2 - z1)
AC = (x3 - x1, y3 - y1, z3 - z1)
Затем вычислим их векторное произведение N следующим образом:
N = AB × AC
Теперь у нас есть нормальный вектор N, который перпендикулярен плоскости, проходящей через точки A, B и C.
Так как плоскость проходит через точку A, мы можем использовать ее координаты в уравнении плоскости:
Nx(x - x1) + Ny(y - y1) + Nz(z - z1) = 0
Таким образом, уравнение плоскости, проходящей через точки A, B и C, может быть записано в виде:
Nxx + Nyy + Nzz - (Nxx1 + Nyy1 + Nzz1) = 0
Таким образом, мы использовали векторное произведение для определения уравнения плоскости, проходящей через три заданные точки в трехмерном пространстве.
Метод построения системы уравнений через координаты точек плоскости

Для того чтобы найти уравнение плоскости, проходящей через три заданные точки, можно использовать метод построения системы уравнений. В систему входят уравнения, которые задают условие прохождения плоскости через каждую из точек.
Пусть даны три точки A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3).
Уравнение плоскости имеет вид: Ax + By + Cz + D = 0, где A, B, C и D - неизвестные коэффициенты, которые нужно найти.
Для нахождения этих коэффициентов, подставим координаты точек A, B и C в уравнение плоскости и получим следующую систему уравнений:
Ax1 + By1 + Cz1 + D = 0
Ax2 + By2 + Cz2 + D = 0
Ax3 + By3 + Cz3 + D = 0
Система имеет четыре неизвестных (A, B, C и D) и три уравнения. Для нахождения решения системы можно воспользоваться методом Крамера или любым другим методом решения системы линейных уравнений.
После нахождения значений A, B, C и D уравнение плоскости будет полностью определено и можно проверить его, подставив координаты точек A, B и C.
Метод построения системы уравнений через координаты точек плоскости позволяет найти уравнение плоскости, проходящей через заданные точки. Этот метод основан на принципе, что плоскость можно определить через три точки, и для этого нужно составить систему уравнений.