Как найти уравнение плоскости по двум точкам и параллельной прямой — подробное руководство и примеры

Уравнение плоскости – это мощный инструмент в математике, который позволяет описывать геометрические объекты в трехмерном пространстве. Важным примером является уравнение плоскости, проходящей через две заданные точки и параллельной заданной прямой.

Чтобы найти уравнение такой плоскости, необходимо знать две точки, через которые она проходит, и параллельную прямую, относительно которой плоскость должна быть параллельной. Следуя определенному алгоритму, вы сможете найти требуемое уравнение и наглядно представить плоскость в пространстве.

Для начала, найдем вектор, задающий направление параллельной прямой. Это можно сделать, взяв два произвольных вектора, лежащих в плоскости, и выполнив их векторное произведение. Затем, используя найденный вектор и координаты одной из точек, мы можем записать уравнение плоскости в виде Ax + By + Cz + D = 0, где A, B, C и D – это коэффициенты, которые мы должны найти.

Как найти уравнение плоскости по двум точкам и параллельной прямой

Уравнение плоскости можно найти, используя две точки и параллельную прямую, проходящую через эти точки. Для этого нужно выполнить следующие шаги:

1. Найдите вектор, направленный от одной точки к другой. Для этого вычтите координаты одной точки из координат другой точки.
2. Найдите вектор, параллельный заданной параллельной прямой. Для этого можно использовать коэффициенты при переменных в уравнении прямой.
3. Найдите векторное произведение найденных векторов. Результат будет вектором, нормальным к плоскости.
4. Используя найденный вектор и координаты одной из точек, составьте уравнение плоскости в виде Ax + By + Cz + D = 0, где A, B и C - координаты вектора, а D - значение левой части уравнения.

Например, пусть есть две точки A(1, 2, 3) и B(4, 5, 6), и параллельная прямая имеет уравнение 2x - 3y + 5z = 10. Сначала найдем вектор направления AB:

AB = B - A = (4, 5, 6) - (1, 2, 3) = (3, 3, 3)

Затем найдем вектор, параллельный прямой:

v = (2, -3, 5)

Вычислим векторное произведение этих векторов:

n = AB × v = (3, 3, 3) × (2, -3, 5) = (24, -3, -9)

Теперь у нас есть вектор, нормальный к плоскости - n = (24, -3, -9). Используя одну из точек, например A(1, 2, 3), составляем уравнение плоскости:

24x - 3y - 9z + D = 0

Подставив координаты точки A, получаем:

24 * 1 - 3 * 2 - 9 * 3 + D = 0

Упрощая, получаем:

24 - 6 - 27 + D = 0

D = 9

Итак, уравнение плоскости, проходящей через точки A(1, 2, 3) и B(4, 5, 6), и параллельной прямой 2x - 3y + 5z = 10, имеет вид:

24x - 3y - 9z + 9 = 0

Выбор двух точек и параллельной прямой

Для нахождения уравнения плоскости, проходящей через две заданные точки и параллельной прямой, необходимо правильно выбрать эти точки и прямую.

Первым шагом выберите две точки, через которые должна проходить плоскость. Эти точки могут быть известными или заданными вам в условии задачи. Важно помнить, что выбранные точки должны быть различными и не совпадать между собой.

Далее, определите параллельную прямую, которая должна быть важной особенностью плоскости. Это может быть прямая, заданная уравнением, геометрическим описанием или любым другим способом, который указан в задаче. Параллельная прямая должна лежать в той же плоскости, что и плоскость, которую вы ищете.

После выбора точек и параллельной прямой, вы можете приступить к нахождению уравнения плоскости. Это можно сделать, используя геометрические или аналитические методы в зависимости от условий задачи.

Важно следовать такому порядку действий и правильно выбирать точки и прямую, чтобы получить правильный ответ. Неправильный выбор точек или прямой может привести к неверному уравнению плоскости или даже к невозможности его найти.

Вычисление векторов и их скалярного произведения

Для вычисления вектора сначала необходимо определить его начало и конец. Начало вектора может быть в точке A(x1, y1, z1), а конец вектора в точке B(x2, y2, z2).

Вектор AB можно вычислить, вычислив разность координат x, y и z:

AB(x2 - x1, y2 - y1, z2 - z1)

Скалярное произведение векторов - это операция, результатом которой является число. Скалярное произведение вычисляется следующим образом:

А * B = |A| * |B| * cos(α)

где |A| и |B| - длины векторов A и B соответственно, α - угол между векторами A и B.

Используя эти формулы, вы можете вычислить векторы и их скалярное произведение для решения задач, связанных с поиском уравнений плоскости по двум точкам и параллельной прямой.

Построение нормали плоскости

Чтобы построить нормаль к плоскости, необходимо знать её уравнение и координаты точки, через которую проходит нормаль. Если уравнение плоскости дано в виде общего уравнения Ax + By + Cz + D = 0, то нормаль к плоскости имеет координаты (A, B, C).

Если уравнение плоскости дано в виде параметрического уравнения, например, в виде точки P0 = (x0, y0, z0), и двух векторов, например, v1 = (a1, b1, c1), и v2 = (a2, b2, c2), параллельных плоскости, то нормаль к плоскости может быть найдена с помощью векторного произведения векторов v1 и v2. Таким образом, нормаль к плоскости будет иметь координаты:

N(AB) = (b1 \* c2 - c1 \* b2, c1 \* a2 - a1 \* c2, a1 \* b2 - b1 \* a2)

Построение нормали плоскости может быть полезно, например, при определении положения точки относительно плоскости или при нахождении проекции точки на плоскость.

Нахождение константного члена уравнения

Для нахождения уравнения плоскости важно знать координаты двух точек и параллельной прямой. После определения координат точек и направления прямой, можно найти константный член уравнения, который обозначается как "d".

В уравнении плоскости общего вида Ax + By + Cz + d = 0, значения коэффициентов A, B и C могут быть найдены путем нахождения нормали плоскости, которая перпендикулярна к плоскости. Нормаль можно найти при помощи векторного произведения двух векторов направления, исходящих из двух точек.

После нахождения нормали плоскости можно использовать любую из двух точек, чтобы найти значение константного члена. Для этого необходимо подставить координаты этой точки и найденные коэффициенты в уравнение плоскости и решить его относительно "d".

Например, пусть даны две точки A(2, 5, 1) и B(3, -1, 4), а также параллельная прямая с направляющим вектором [1, -2, 3].

1. Найдем нормаль плоскости N при помощи векторного произведения направляющего вектора параллельной прямой и вектора, составленного из координат точек A и B:

N = [1, -2, 3] × [(3-2), (-1-5), (4-1)] = [1, -2, 3] × [1, -6, 3] = [6, 0, -8]

2. Подставим координаты точки A(2, 5, 1) и найденные коэффициенты в уравнение плоскости Ax + By + Cz + d = 0:

6 * 2 + 0 * 5 + (-8) * 1 + d = 0

12 - 8 + d = 0

d = -4

Таким образом, уравнение плоскости, проходящей через точки A(2, 5, 1) и B(3, -1, 4), и параллельной прямой с направляющим вектором [1, -2, 3], будет иметь вид:

6x - 8z - 4 = 0

Пример вычисления уравнения плоскости

Предположим, что нам даны две точки A(1, 2, 3) и B(4, 5, 6), а также известно, что искомая плоскость параллельна прямой, проходящей через точку C(7, 8, 9) и имеющей направляющий вектор \vec{v} = (2, 1, 3).

Для нахождения уравнения плоскости, необходимо воспользоваться формулой общего уравнения плоскости:

Ax + By + Cz + D = 0

где (A, B, C) - вектор нормали плоскости, a D - свободный член.

Для начала найдем направляющий вектор плоскости, который будет перпендикулярен вектору \vec{v} и, следовательно, параллелен плоскости:

\vec{n} = \vec{v} \times \vec{AB}

где \vec{AB} = \vec{B} - \vec{A} = (4 - 1, 5 - 2, 6 - 3) = (3, 3, 3).

Вычисляя векторное произведение, получаем:

\vec{n} = (2, 1, 3) \times (3, 3, 3) = (3, -3, 3)

Таким образом, вектор нормали плоскости равен \vec{n} = (3, -3, 3).

Подставив найденные значения в формулу общего уравнения плоскости, получим:

3x - 3y + 3z + D = 0

Для дальнейших вычислений подставим координаты одной из известных точек, например, точки A(1, 2, 3):

3(1) - 3(2) + 3(3) + D = 0

3 - 6 + 9 + D = 0

Решая данное уравнение, найдем D:

D = -6

Подставив значение D в общее уравнение плоскости, получим итоговое уравнение:

3x - 3y + 3z - 6 = 0

Таким образом, уравнение плоскости, проходящей через точки A(1, 2, 3) и B(4, 5, 6) и параллельной прямой через C(7, 8, 9) с направляющим вектором \vec{v} = (2, 1, 3), будет иметь вид 3x - 3y + 3z - 6 = 0.

Дополнительные способы определения плоскости

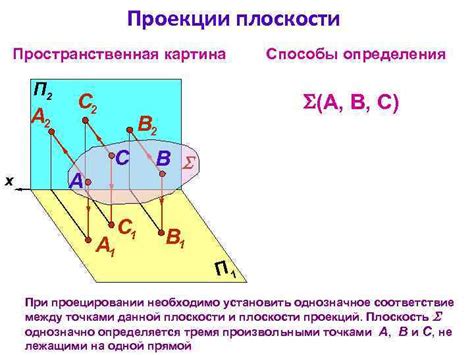
Кроме способа определения плоскости по двум точкам и параллельной прямой, существуют и другие методы нахождения уравнения плоскости.

1. По нормальному вектору и произвольному точечному вектору.

Если известен нормальный вектор плоскости \(\vec{N}\) и произвольный точечный вектор плоскости \(\vec{r}\), то уравнение плоскости можно записать следующим образом:

\[\vec{N} \cdot (\vec{r} - \vec{r_0}) = 0\],

где \(\vec{r_0}\) - координаты произвольной точки на плоскости.

2. По трём не коллинеарным точкам.

Если известны координаты трех точек \((x_1, y_1, z_1)\), \((x_2, y_2, z_2)\) и \((x_3, y_3, z_3)\), не лежащих на одной прямой, то уравнение плоскости можно записать в виде:

\[(x - x_1)(y_2 - y_1)(z_3 - z_1) + (x - x_2)(y_3 - y_2)(z_1 - z_2) + (x - x_3)(y_1 - y_3)(z_2 - z_3) = 0\].

3. По точке и двум векторам на плоскости.

Если известны координаты точки \((x_0, y_0, z_0)\) на плоскости и два вектора \(\vec{a}\) и \(\vec{b}\), лежащие в плоскости, то уравнение плоскости можно записать с помощью векторного произведения:

\[\vec{a} \cdot (\vec{r} - \vec{r_0}) \times \vec{b} = 0\],

где \(\vec{r}\) - точечный вектор плоскости, а \(\vec{r_0}\) - координаты точки на плоскости.

Знание этих дополнительных способов определения плоскости позволяет решать более сложные задачи по построению и анализу трехмерных моделей и конструкций.

Задачи на определение плоскости по двум точкам и параллельной прямой

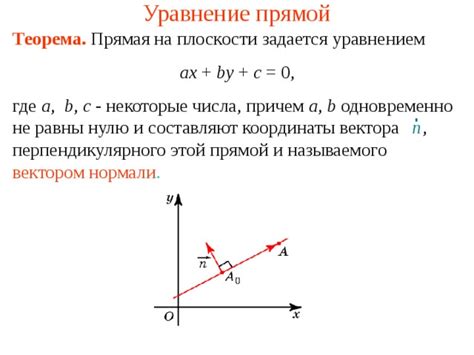
Для решения задачи на определение плоскости по двум точкам и параллельной прямой необходимо следовать нескольким шагам. Вначале нужно найти направляющий вектор плоскости, используя векторы, полученные из координат двух заданных точек. Затем можно найти уравнение плоскости, используя полученный направляющий вектор и координаты одной из точек.

Прежде чем приступить к решению задачи, полезно упражняться на примерах. Рассмотрим несколько примеров задач на нахождение уравнения плоскости по двум точкам и параллельной прямой:

Пример 1:

Найдите уравнение плоскости, проходящей через точки A(1, 2, 3) и B(4, 5, 6) и параллельной прямой с уравнением x = 2t, y = 3t, z = 4t.

Решение:

Найдем вектор AB, который будет направляющим вектором плоскости:

AB = (4 - 1, 5 - 2, 6 - 3) = (3, 3, 3)

Также найдем произвольную точку на прямой, например, когда t = 0:

P(2 * 0, 3 * 0, 4 * 0) = (0, 0, 0)

Теперь можем записать уравнение плоскости в виде:

3(x - 0) + 3(y - 0) + 3(z - 0) = 0

Упростим уравнение и получим окончательно:

x + y + z = 0

Таким образом, уравнение плоскости, проходящей через точки A(1, 2, 3) и B(4, 5, 6) и параллельной прямой с уравнением x = 2t, y = 3t, z = 4t, будет x + y + z = 0.

Пример 2:

Найдите уравнение плоскости, проходящей через точки A(3, -1, 2) и B(-2, 4, 7) и параллельной прямой с уравнением x = t, y = 2t, z = 3t.

Решение:

Найдем вектор AB:

AB = (-2 - 3, 4 - (-1), 7 - 2) = (-5, 5, 5)

Возьмем теперь произвольную точку на прямой, когда t = 0:

P(0, 2 * 0, 3 * 0) = (0, 0, 0)

Уравнение плоскости будет иметь вид:

-5(x - 0) + 5(y - 0) + 5(z - 0) = 0

Упростим уравнение и получим окончательно:

-5x + 5y + 5z = 0

Таким образом, уравнение плоскости, проходящей через точки A(3, -1, 2) и B(-2, 4, 7) и параллельной прямой с уравнением x = t, y = 2t, z = 3t, будет -5x + 5y + 5z = 0.

После решения нескольких примеров задач на нахождение плоскости по двум точкам и параллельной прямой, можно убедиться, что данный подход достаточно эффективен и позволяет быстро определить уравнение плоскости, используя только заданные точки и прямую.