Уравнение прямой – это одно из основных понятий геометрии, которое используется для описания линии, проходящей через две заданные точки. Знание этой концепции полезно во многих областях, от математики до физики. В этом руководстве мы расскажем, как найти уравнение прямой, проходящей через две точки на плоскости.
Чтобы найти уравнение прямой через две заданные точки, вам понадобятся координаты этих точек. Обозначим эти точки как P(x1, y1) и Q(x2, y2). Затем мы можем использовать формулу уравнения прямой, которая выглядит следующим образом:
y - y1 = \frac{y2 - y1}{x2 - x1}(x - x1)
В этой формуле x1, y1 и x2, y2 - это координаты наших точек P и Q соответственно, а x и y - это произвольные переменные, представляющие точки на прямой.
Когда мы заполним значениями координат наши точки P и Q, у нас будет уравнение прямой, которое проходит через эти две точки. Теперь мы можем использовать это уравнение для решения различных задач геометрии и физики.
Определение координат
Для определения уравнения прямой через две заданные точки необходимо знать их координаты.
Каждая точка в двумерном пространстве имеет две координаты: x (абсцисса) и y (ордината). На координатной плоскости абсцисса обозначается по горизонтали, а ордината - по вертикали.
При записи координат точки используется следующий формат: (x, y), где x - значение абсциссы, а y - значение ординаты.
Например, точка A с координатами (2, 5) имеет абсциссу 2 и ординату 5.
Чтобы найти уравнение прямой, проходящей через две точки A(x1, y1) и B(x2, y2), необходимо знать их координаты. Тогда координаты точек можно использовать в уравнении прямой для определения ее углового коэффициента и точки пересечения с осями координат.
Используя формулу для определения углового коэффициента прямой (k = Δy / Δx), где Δx = x2 - x1 и Δy = y2 - y1, и известную точку A(x1, y1), можно найти уравнение прямой вида y = kx + b.
Таким образом, с использованием координат точек A и B и знания формулы для углового коэффициента, можно найти уравнение прямой, проходящей через эти точки, а именно: y = kx + b, где k - угловой коэффициент, b - точка пересечения с осью ординат.
Найти расстояние между точками
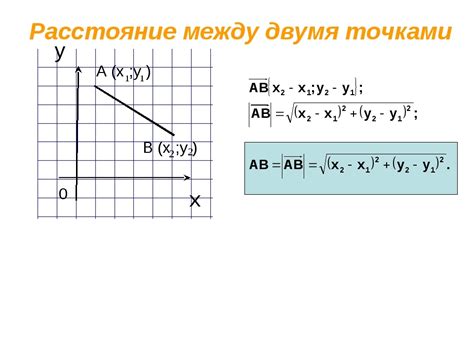
Для решения данной задачи можно воспользоваться формулой расстояния между двумя точками в прямоугольной системе координат:
d = √((x2 - x1)^2 + (y2 - y1)^2)
где (x1, y1) и (x2, y2) - координаты заданных точек.
Для вычисления расстояния между точками, следует заменить соответствующие значения в формуле и выполнить необходимые математические операции.
Приведем пример:
Пусть заданы точки A(3, 4) и B(7, 2). Для нахождения расстояния между этими точками подставим соответствующие значения в формулу:
d = √((7 - 3)^2 + (2 - 4)^2)
d = √(4^2 + (-2)^2)
d = √(16 + 4)
d = √20
d = 4.47
Таким образом, расстояние между точками A(3, 4) и B(7, 2) равно 4.47 единицы длины.
Найти угол между точками

Чтобы найти угол между двумя заданными точками на плоскости, нужно использовать формулу для вычисления угла, основанную на координатах этих точек. Воспользуемся формулой для нахождения угла между двумя векторами по их координатам.
Пусть у нас есть две точки на плоскости: A(x1, y1) и B(x2, y2). Мы можем вычислить векторы AB и AX, где X - некоторая точка на продолжении прямой AB. Затем, используя формулу для вычисления угла между векторами, мы найдем значение угла между отрезком AB и осью X.
Давайте приведем пример:
| Точка | x | y |
|---|---|---|
| A | x1 | y1 |
| B | x2 | y2 |
Чтобы найти угол между точками A и B, нужно выполнить следующие шаги:
- Вычислить разности координат по каждой оси: dx = x2 - x1 и dy = y2 - y1.
- Найти угол между вектором AB и осью X: angle = atan2(dy, dx).
- Угол будет измеряться в радианах. Если вам нужно его представить в градусах, просто умножьте его на 180/π: angle_degrees = angle * 180/π.
Теперь у вас есть угол между точками A и B на плоскости. Не забывайте, что угол может быть положительным или отрицательным, и его значение определяется поворотом отрезка AB в противоположных направлениях. Если вы хотите получить положительное значение угла, добавьте 360°.
Построение уравнения прямой

Для начала рассмотрим случай, когда прямая вертикальна, то есть x1 = x2. В этом случае уравнение прямой имеет вид x = x1.
Если прямая невертикальна, то можно использовать общее уравнение прямой, которое имеет вид y = mx + b, где m – это коэффициент наклона прямой (указывает ее угол наклона), а b – свободный член (определяет смещение прямой по вертикальной оси).
Для нахождения коэффициента наклона (m) используем формулу:
m = (y2 - y1) / (x2 - x1)
Подставляя найденные значения x1, x2, y1, и y2 в уравнение прямой, получаем конкретное уравнение прямой, которая проходит через заданные точки.