Ускорение – одна из основных физических величин, описывающих движение тела. Оно определяет скорость изменения скорости и может быть измерено по различным параметрам, включая высоту и время. Определение ускорения по высоте и времени важно для понимания динамики движения тела и использования его в различных отраслях науки и техники.
Существует несколько методов, которые позволяют найти ускорение по высоте и времени. Один из них – использование формулы ускорения свободного падения. Формула ускорения свободного падения позволяет определить ускорение тела при свободном падении, когда на него не действуют другие силы, кроме силы тяжести.
Если известна высота, на которой находится тело, и время, за которое оно перемещается на эту высоту, то ускорение можно найти с помощью следующей формулы: ускорение = (2 * высота) / (время^2). В этой формуле высота указывается в метрах, а время – в секундах. Например, если высота равна 10 метрам, а время – 2 секундам, то ускорение будет равно (2 * 10) / (2^2) = 20 / 4 = 5 м/с^2.
Определение понятий

Перед тем как перейти к рассмотрению методов и примеров расчета ускорения по высоте и времени, необходимо понять основные понятия, связанные с этой темой.
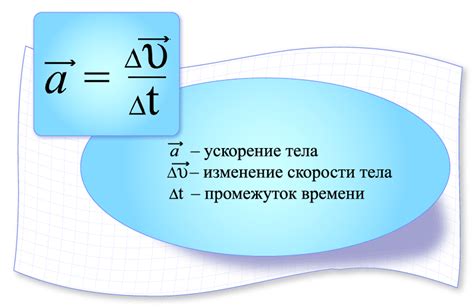
- Ускорение - это векторная физическая величина, которая определяет изменение скорости объекта за определенный промежуток времени. Ускорение может быть положительным (увеличивает скорость) или отрицательным (уменьшает скорость).
- Высота - это вертикальное расстояние от поверхности Земли или другого объекта до точки, на которой находится объект. Высота может быть измерена в метрах, футах или других единицах длины.
- Время - это параметр, используемый для измерения длительности процессов и событий. В физике время обычно измеряется в секундах.
Понимание этих основных понятий поможет в дальнейшем разбираться в методах расчета ускорения по высоте и времени, а также применять их на практике.
Методы расчета ускорения по высоте и времени
Один из наиболее простых методов - это использование формулы для расчета среднего ускорения. Для этого необходимо измерить начальную и конечную высоты объекта, а также время, за которое объект прошел данный интервал высоты. По формуле:
ускорение = (конечная высота - начальная высота) / время
Этот метод подходит для расчета ускорения объектов, движущихся вниз или вверх с постоянной скоростью.
Если объект движется с переменной скоростью, то следует использовать другой метод - графический. Для этого необходимо построить график зависимости высоты от времени и затем найти наклон кривой на интересующем интервале. Наклон показывает значение ускорения на этом участке движения.
Еще один метод - это использование уравнения равноускоренного движения. В этом случае необходимо знать начальную скорость объекта, время его движения и конечную высоту. По формуле:
ускорение = (конечная скорость - начальная скорость) / время
Этот метод позволяет учесть изменение скорости объекта по мере его движения.
Таким образом, существует несколько методов расчета ускорения по высоте и времени, которые выбираются в зависимости от условий движения объекта.
Первый метод: использование формулы среднего значения

Для определения ускорения по высоте и времени можно использовать формулу среднего значения. Этот метод основан на вычислении изменения высоты и времени, и последующем делении изменения высоты на изменение времени.
Формула для определения ускорения по высоте выглядит следующим образом:
| Формула | Описание |
|---|---|
| ah = Δh / Δt | Ускорение по высоте (ah) равно изменению высоты (Δh) разделенному на изменение времени (Δt) |
Где:
- ah - ускорение по высоте
- Δh - изменение высоты
- Δt - изменение времени
Для примера, предположим, что объект движется вверх под действием тяги ракеты. Начальная высота объекта равна 0 метров, а конечная высота равна 100 метров. Время, за которое объект достигает конечной высоты, равно 10 секундам. Используя формулу, можно вычислить ускорение по высоте:
| Дано | Значение |
|---|---|
| Δh | 100 м |
| Δt | 10 с |
Применяя формулу, получим:
ah = 100 м / 10 с = 10 м/с²
Таким образом, ускорение по высоте равно 10 м/с². Это означает, что объект движется вверх со скоростью 10 метров в секунду в квадрате.
Второй метод: использование уравнения движения

Уравнение движения связывает ускорение, начальную скорость, время и пройденное расстояние в вертикальном направлении. В общем виде оно выглядит следующим образом:
h = ut + (1/2)gt^2
где:
- h - пройденное расстояние в вертикальном направлении (высота);
- u - начальная скорость в вертикальном направлении;
- g - ускорение свободного падения;
- t - время.
Если известны начальная скорость, время и пройденное расстояние, то уравнение можно переставить и найти ускорение:
g = (2h - 2ut) / t^2
Пример использования этого метода:
- Измерьте начальную высоту (h) и начальную скорость вверх (u).
- Запустите таймер и отпустите тело.
- Измерьте время (t), за которое тело достигло конечной высоты.
- Подставьте известные значения в уравнение и решите его, чтобы найти ускорение (g).
Этот метод позволяет получить более точные результаты, так как учитывает не только время и пройденное расстояние, но и начальную скорость. Он особенно полезен, когда начальная скорость не равна нулю.
Третий метод: использование интеграла

Для использования интеграла необходимо знать функцию, описывающую зависимость высоты от времени. Обозначим эту функцию как h(t), где h - высота, а t - время.
Для определения ускорения по высоте можно воспользоваться следующей формулой:
a = -\frac{d^2h}{dt^2}
где a - ускорение, а d^2h/dt^2 - вторая производная функции h(t) по времени.
Для нахождения второй производной можно воспользоваться интегралом в отношении времени:
d^2h = \int_{0}^{t} \frac{d^2h}{dt^2} dt
Таким образом, для определения ускорения по высоте можно взять интеграл от второй производной функции h(t) по времени от нуля до заданного момента времени.
Пример:
Пусть функция h(t) = 3t^2 + 2t + 1 описывает зависимость высоты от времени. Найдем ускорение по высоте в момент времени t = 2.
Сначала найдем вторую производную:
\frac{d^2h}{dt^2} = \frac{d}{dt}(6t + 2) = 6
Затем возьмем интеграл от второй производной по времени от нуля до t = 2:
\int_{0}^{2} 6 dt = 6t \Big|_0^2 = 6\cdot2 - 6\cdot0 = 12
Таким образом, ускорение по высоте в момент времени t = 2 равно 12.
Примеры решения задач по нахождению ускорения по высоте и времени

Для решения задач по нахождению ускорения по высоте и времени необходимо использовать уравнение движения объекта в вертикальном направлении.
Например, пусть у нас есть задача следующего вида: тело брошено вертикально вверх из точки A с начальной скоростью 10 м/с. Через 4 секунды оно достигло вершины траектории точки B. Каково ускорение тела по высоте и время его полета?
Для начала, найдем ускорение по формуле:
a = (v - u) / t
где a - ускорение, v - конечная скорость, u - начальная скорость, t - время движения.
Определим известные данные: начальная скорость u = 10 м/с, конечная скорость v = 0 м/с (так как тело достигло максимальной высоты и начало падать), время движения t = 4 сек.
Подставим значения в формулу и найдем ускорение:
a = (0 - 10) / 4 = -2.5 м/с²
Ускорение получается отрицательным, так как тело движется вверх до максимальной высоты и затем начинает падать под действием силы тяжести.
Теперь найдем время полета тела. Для этого воспользуемся формулой:
T = 2t
где T - время полета (время, за которое тело пройдет весь путь), t - время движения в одном направлении.
Подставляем значение времени движения и находим время полета:
T = 2 * 4 = 8 сек
Таким образом, ускорение по высоте равно -2.5 м/с², а время полета составляет 8 секунд.