Векторное произведение – одна из основных операций векторной алгебры, которая позволяет найти новый вектор, перпендикулярный двум заданным векторам. Эта операция особенно полезна в трехмерном пространстве, где мы имеем возможность задать три вектора, составляющих плоскость, и однозначно определить вектор, перпендикулярный этой плоскости.
Для нахождения векторного произведения в трехмерном пространстве по координатам необходимо использовать правило правой руки или определительную формулу. Следуя этим правилам, мы можем найти длину вектора и его координаты. Векторное произведение часто применяется в различных областях, включая физику, геометрию, механику, графику и другие.
Важно отметить, что векторное произведение двух векторов является вектором, сонаправленным с нормалью к плоскости, образованной этими векторами. Его длина равна произведению длин векторов на синус угла между ними. Координаты вектора можно найти с помощью определителя матрицы, составленной из координат исходных векторов.
Как найти векторное произведение в трехмерном пространстве

Для нахождения векторного произведения двух векторов, мы можем использовать следующую формулу:
A × B = [(AyBz - AzBy), (AzBx - AxBz), (AxBy - AyBx)]
Где A и B – исходные векторы, а Ax, Ay, Az и Bx, By, Bz – их координаты соответственно.
Применение этой формулы позволяет найти вектор, который перпендикулярен исходным векторам A и B. Модуль векторного произведения равен произведению длин исходных векторов на синус угла между ними.
Векторное произведение в трехмерном пространстве имеет свои особенности. Оно не коммутативно, то есть A × B = -B × A. Также векторное произведение параллельных векторов равно нулю.
Векторное произведение играет важную роль в геометрии, механике и физике. Зная его свойства и способ вычисления, мы можем решать задачи с использованием векторных операций и получать точные результаты.
Способы вычисления векторного произведения в трехмерном пространстве
Существует несколько способов вычисления векторного произведения:
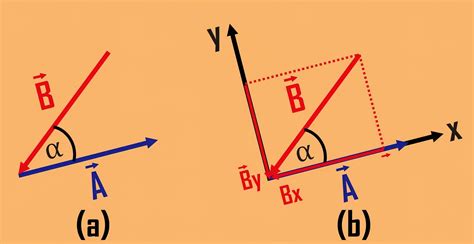
1. Геометрический подход: При использовании геометрического подхода векторное произведение можно представить как произведение модулей исходных векторов на синус угла между ними. Направление полученного вектора определяется с помощью правила правой руки.
2. Алгебраический подход: При использовании алгебраического подхода векторное произведение можно вычислить с помощью определителя матрицы, составленной из координат исходных векторов. Результатом будет вектор, компоненты которого будут выражены через координаты исходных векторов.
3. Векторный подход: Векторное произведение можно вычислить с помощью векторного умножения компонент по формуле: (a2 * b3 - a3 * b2)i + (a3 * b1 - a1 * b3)j + (a1 * b2 - a2 * b1)k. Результат будет новым вектором, перпендикулярным к исходным векторам и задаваемым его компонентами.
Выбор способа вычисления векторного произведения зависит от конкретной задачи и предпочтений пользователя. Все эти методы эквивалентны и дадут одинаковый результат.