Вероятность - это важное понятие как в математике, так и в повседневной жизни. Иногда нам требуется определить вероятность события, когда у нас нет информации о полном количестве возможных исходов. Несмотря на то, что это может показаться сложным, существуют методы и подходы, которые помогут нам найти вероятность при неизвестном общем количестве. В этой статье рассмотрим несколько полезных советов и методов, которые помогут вам в этой задаче.

Первым шагом в определении вероятности при неизвестном общем количестве является сбор данных. Найдите все доступные информационные источники, которые могут быть связаны с вашим событием, и соберите данные, которые могут помочь вам в определении вероятности. Например, если вы хотите определить вероятность выпадения определенной стороны монеты, можете провести серию экспериментов и записать результаты.

После сбора данных вы можете использовать эти данные для определения вероятности. Существует несколько подходов к этому. Во-первых, вы можете использовать относительную частоту. Разделите количество желаемых исходов на общее количество исходов и умножьте на 100%, чтобы найти вероятность в процентах. Например, если у вас есть 20 голубых и 30 красных шаров в урне, вероятность вытащить голубой шар будет 20/50 * 100% = 40%.

Вторым подходом является использование статистического анализа. Если у вас есть достаточно данных, вы можете использовать статистические методы, такие как доверительные интервалы и регрессионный анализ, чтобы определить вероятность. Эти методы могут быть сложными и требовать математических знаний, но они могут быть очень полезными при работе с большим объемом данных.

Наконец, не забывайте о важности использования здравого смысла при определении вероятности при неизвестном общем количестве. Используйте свой жизненный и профессиональный опыт, чтобы сделать предположения и оценить вероятность события. Помните, что вероятность - это всего лишь предсказание, основанное на доступных данных, и она может измениться в зависимости от новых фактов и обстоятельств.

Методы и советы для нахождения вероятности в случае неизвестного общего количества

1. Статистический подход

Если у вас нет точной информации о общем количестве элементов, но у вас есть некоторая выборка, вы можете использовать статистический подход для нахождения вероятности.

Для этого вам нужно определить, сколько элементов из выборки соответствуют вашему условию, и поделить эту цифру на размер выборки. Например, если у вас есть выборка из 100 элементов, и 20 из них соответствуют вашему условию, то вероятность будет равна 20/100, или 0,2.

2. Использование априорной информации

Если у вас есть некоторая априорная информация о общем количестве элементов, вы можете использовать ее для приближенного расчета вероятности.

Например, если вы знаете, что в вашем городе проживает около 500 тысяч человек, и вы хотите узнать вероятность встретить своего друга в торговом центре, вы можете использовать это число в качестве оценки общего количества. Затем, вы можете использовать статистический подход для нахождения вероятности.

3. Использование метода случайной выборки

Если у вас нет никакой информации о общем количестве элементов, и вы не можете оценить его, вы можете использовать метод случайной выборки для нахождения вероятности.

Для этого вам нужно произвести случайную выборку из возможных элементов и посчитать, сколько из них соответствуют вашему условию. Затем, вы можете использовать статистический подход, описанный выше, для нахождения вероятности.

4. Итеративный подход

Если у вас есть несколько выборок, которые могут представлять различные аспекты или подгруппы общего количества, вы можете использовать итеративный подход для нахождения вероятности.

Например, если у вас есть выборки, представляющие различные возрастные группы, вы можете использовать статистический подход для нахождения вероятности в каждой группе и затем усреднить полученные результаты.

Используя эти методы и советы, вы можете приближенно находить вероятность в случае неизвестного общего количества. Важно помнить, что результаты полученные таким образом будут лишь приближенными и могут содержать погрешности, связанные с использованными методами и оценками.

Определите общую вероятность по частичным данным

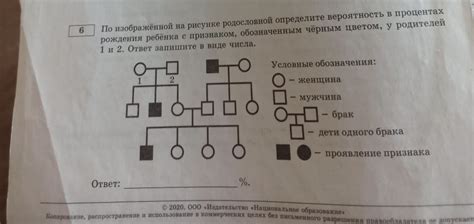
В задачах, где общее количество элементов неизвестно, найти вероятность может быть сложно. Однако, с помощью частичных данных можно получить представление о общей вероятности. В этом разделе мы рассмотрим несколько полезных советов и методов для определения общей вероятности по частичным данным.

Первым шагом является анализ имеющихся данных. Изучите все доступные информации о вероятности конкретного события или выпадения определенного результата. Обратите внимание на тот факт, что некоторые данные могут быть представлены в виде относительных вероятностей, а другие - в виде абсолютных значений.

Далее, используйте изученные данные для вычисления относительных вероятностей других событий или результатов. Для этого можно использовать правило сложения или умножения вероятностей, в зависимости от конкретной ситуации.

Кроме того, при анализе частичных данных необходимо принять во внимание возможные условия или ограничения, которые могут повлиять на общую вероятность. Например, если известно, что события являются независимыми, то можно применить правило умножения вероятностей. Если же события зависимы, то нужно использовать формулу условной вероятности.

Наконец, важно помнить, что оценка общей вероятности на основе частичных данных может иметь некоторую погрешность и быть приближенной. Однако, даже приближенный результат может быть полезным для принятия решений или анализа ситуации.

Итак, если у вас есть только частичные данные, пользуйтесь ими максимально возможно. Анализируйте информацию, вычисляйте относительные вероятности и принимайте во внимание возможные условия. В результате вы сможете получить представление о общей вероятности, даже не зная точного общего количества элементов.

Используйте метод максимального правдоподобия

Для применения метода максимального правдоподобия, необходимо предположить функцию, которая описывает распределение данных. Затем с помощью этой функции строится функция правдоподобия - вероятность получить наблюдаемые данные при заданных параметрах. Цель метода - найти такие значения параметров, при которых функция правдоподобия будет максимальна.

Процесс поиска максимума функции правдоподобия можно выполнить различными методами оптимизации, например, методом наискорейшего спуска или методом Флетчера-Ривса.

Метод максимального правдоподобия является очень мощным инструментом для оценки параметров вероятностных моделей, особенно когда общее количество элементов неизвестно. Однако, для его применения необходимо корректно определить функцию, описывающую распределение данных, и иметь достаточное количество наблюдений.

Пользуясь методом максимального правдоподобия, вы сможете более точно оценить вероятность при неизвестном общем количестве элементов и принять более обоснованные решения в соответствующих ситуациях.

Примените статистический метод Байеса

Если у вас есть неизвестное общее количество и вы хотите найти вероятность, применение статистического метода Байеса может быть полезным. Метод Байеса основан на теореме Байеса, которая позволяет обновить вероятность гипотезы на основе новой информации.

Для применения метода Байеса необходимо иметь базовую вероятность, изначальную гипотезу и новую информацию. Затем вы можете использовать формулу Байеса для обновления вероятности и получения нового результата. Формула Байеса выглядит следующим образом: P(A|B) = (P(B|A) * P(A)) / P(B), где P(A|B) - вероятность гипотезы A при наличии информации B, P(B|A) - вероятность информации B при наличии гипотезы A, P(A) - изначальная вероятность гипотезы A, P(B) - вероятность информации B.

Применение метода Байеса может быть полезным для оценки вероятности при неизвестном общем количестве. Например, если вы хотите узнать вероятность того, что выбранный случайным образом студент вашей школы имеет оценку "Отлично" на экзамене, вы можете использовать метод Байеса, чтобы обновить вероятность на основе информации о других студентах и их оценках.

Важно помнить, что результат применения метода Байеса зависит от качества и точности начальных данных и новой информации. Чем более точные и надежные данные вы используете, тем более точный будет результат. Также стоит учитывать, что метод Байеса не является единственным методом оценки вероятности и его применимость может зависеть от конкретной ситуации.

В заключении, применение статистического метода Байеса может быть полезным при поиске вероятности при неизвестном общем количестве. Он позволяет обновить вероятность гипотезы на основе новой информации и может быть полезным инструментом в анализе данных.

Рассмотрите принцип комбинаторики

Существуют два основных принципа комбинаторики: принцип суммы и принцип произведения.

Принцип суммы применяется в ситуациях, когда рассматривается несколько независимых событий. Для определения вероятности таких событий необходимо сложить вероятности каждого из них.

Принцип произведения используется в случаях, когда рассматривается последовательность зависимых событий. Для определения вероятности таких событий необходимо перемножить вероятности каждого из них.

Например, если нужно определить вероятность выбрать 3 мяча из урны, содержащей 10 мячей неизвестного цвета, принцип произведения может быть использован следующим образом. Первый шаг - определить вероятность выбрать первый мяч. Затем, учитывая, что количество мячей в урне уменьшается на 1 после каждого выбора, определить вероятность выбрать второй мяч. Наконец, определить вероятность выбрать третий мяч. Полученные вероятности можно перемножить, чтобы найти итоговую вероятность.

Применение принципа комбинаторики позволяет систематично рассмотреть все возможные комбинации и перестановки объектов или элементов, что значительно erleichtert den Prozess der Berechnung der Wahrscheinlichkeit bei unbekannter Gesamtzahl. Обязательно учтите принцип комбинаторики при решении задач, связанных с определением вероятности при неизвестном общем количестве.

Обратитесь к теории множеств

Когда нам известно только общее количество элементов, а не сами элементы, мы можем обратиться к теории множеств для нахождения вероятности. Теория множеств изучает различные комбинации и связи между множествами, что может быть очень полезным при расчете вероятностей в таких случаях.

Чтобы применить теорию множеств, мы должны знать несколько основных понятий:

1. Универсальное множество (U): это множество, которое содержит все возможные элементы. Оно является контекстом для всех остальных множеств.
2. Событие (A): это множество определенных элементов или исходов, на которые мы хотим посчитать вероятность.
3. Вероятность (P): это отношение количества благоприятных исходов к общему количеству возможных исходов.

Когда у нас нет информации о самих элементах, но есть общее количество, мы можем использовать операции над множествами, такие как объединение, пересечение и разность, для нахождения вероятностей. Например, если у нас есть два множества A и B, и нам нужно найти вероятность того, что событие A или событие B произойдет, мы можем использовать формулу:

Операция "или" представляет собой объединение множеств, операция "и" - пересечение множеств. Разность множеств может использоваться для учета уже учтенных элементов.

Теория множеств также может быть использована для решения других возможных задач, связанных с вероятностью при неизвестном общем количестве, например, нахождение вероятности при сложном условном событии или при наличии нескольких независимых событий.

Важно помнить, что теория множеств является одним из инструментов для расчета вероятности в таких ситуациях и может быть применена только при определенных условиях. Поэтому важно убедиться, что вы правильно определили множества и используете соответствующие операции для решения задачи.

Возьмите данные из предыдущих исследований

Если вы столкнулись с задачей определения вероятности при неизвестном общем количестве, полезным может оказаться анализ предыдущих исследований. Исследования похожих ситуаций или аналогичных областей могут дать вам ценные данные и информацию о вероятностях.

Прежде всего, обратитесь к научным статьям, журналам, отчетам и публикациям, связанным с вашей проблемой. Обращайте особое внимание на исследования, проведенные в схожих условиях или с использованием схожих методов. Просмотрите результаты и выделите те данные, которые могут быть применимы к вашей ситуации.

Кроме того, обратитесь к официальным статистическим данным и базам данных в вашей области. Государственные и международные организации могут иметь статистику и информацию, которая может быть полезна при определении вероятности при неизвестном общем количестве. Такие данные могут содержать информацию о предыдущих исследованиях, тенденциях и распределении.

Помимо официальных исследований, возможно, стоит обратиться к литературе и примерам из практики. Книги, статьи и публикации в масс-медиа могут предоставить вам полезные примеры и истории, которые могут быть применимы к вашей задаче. Используйте дополнительные источники информации для подтверждения и уточнения данных, найденных в научных исследованиях.

Важно помнить, что данные из предыдущих исследований являются основой для определения вероятности, но не являются абсолютно точными. Вам необходимо проанализировать источники данных, учитывать контекст и принять во внимание возможные ограничения или изменения условий. Всегда оценивайте надежность и достоверность данных из предыдущих исследований и применяйте их с учетом конкретной ситуации.

Используйте модель случайных величин

Ключевым шагом при использовании модели случайных величин является определение возможных значений, которые может принимать неизвестное общее количество. Затем необходимо привести эти значения в виде дискретной случайной величины, которая может принимать только определенные значения.

Далее следует оценить вероятности каждого значения случайной величины на основе доступной информации или с помощью специальных методов. Можно использовать статистические данные, результаты предыдущих исследований или экспертные оценки.

После того, как были определены вероятности для каждого значения случайной величины, возможно определить общую вероятность для конкретного события или группы событий. Для этого необходимо сложить вероятности соответствующих значений случайной величины.

Таким образом, использование модели случайных величин позволяет структурировать информацию о неизвестном общем количестве и оценить вероятности различных исходов. Это помогает принимать рациональные решения и предсказывать результаты на основе вероятностных расчетов.

Примените аналитический подход

Когда вы сталкиваетесь с задачей по вычислению вероятности с неизвестным общим количеством, полезно применить аналитический подход. Этот подход основан на использовании логических размышлений и математических методов для нахождения вероятности.

Для применения аналитического подхода следуйте следующим шагам:

1. Определите все возможные исходы события.
2. Разбейте исходы на группы с одинаковой вероятностью.
3. Примените формулы для вычисления вероятности.
4. Учтите все возможные вариации и комбинации.

Аналитический подход позволяет найти вероятность при неизвестном общем количестве, полагаясь на логику и математический анализ. Он особенно полезен в задачах, где нет возможности провести эксперимент или подсчитать все возможные исходы. Применяя аналитический подход, вы сможете получить более точные и строго обоснованные результаты.