Вероятность – одно из ключевых понятий, которое используется во многих областях жизни. Будь то игры, экономика или наука, понимание вероятности позволяет принимать взвешенные решения и предсказывать исходы событий.
Но как же найти вероятность конкретного события? В этой статье мы рассмотрим несколько простых шагов, которые помогут вам разобраться в этой теме и использовать вероятность в своих расчетах.
Вероятность события выражается числом от 0 до 1, где 0 означает невозможность события, а 1 – его абсолютную достоверность. Для расчета вероятности существуют различные формулы и методы, в зависимости от типа задачи.
Определение и основные понятия
Событие - это возможный исход эксперимента или ситуации. События бывают простые и составные. Простое событие - это событие, которое невозможно разделить на более мелкие части. Составное событие - это событие, которое состоит из двух или более простых событий.
Эксперимент - это ситуация или действие, которое может привести к определенным исходам. Например, бросание монеты - это эксперимент, который может иметь два исхода: выпадение орла или выпадение решки.
Пространство элементарных событий - это множество всех возможных исходов эксперимента. Каждый исход является элементарным событием и имеет определенную вероятность произойти.
- Случайная величина - это функция, которая отображает элементарные события в числа.
- Вычисление вероятности - проведение действий и использование формулы, позволяющей определить степень уверенности в наступлении события.
- Относительная частота - это частота, с которой происходит определенное событие в серии повторяющихся экспериментов.
- Сложение вероятностей - это операция, которая позволяет определить вероятность наступления одного из нескольких событий.
- Умножение вероятностей - это операция, которая позволяет определить вероятность наступления двух или более событий, связанных между собой.
Расчет вероятности события по формуле классической вероятности
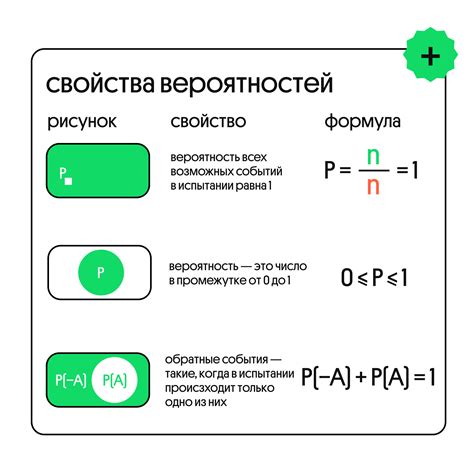
Для расчета вероятности события по формуле классической вероятности необходимо выполнить следующие шаги:
- Определить все возможные исходы события.
- Определить количество благоприятных исходов.
- Рассчитать вероятность события по формуле классической вероятности: вероятность = количество благоприятных исходов / количество всех возможных исходов.
Пример:
Допустим, мы выбираем одну карту из стандартной колоды в 52 карты. Исходом может быть выбор любой карты из колоды.
1. Всего возможных исходов равно 52 (так как в колоде 52 карты).
2. Благоприятными исходами могут быть все карты одной масти (например, пиковая масть), и их количество равно 13 (так как в каждой масти 13 карт).
3. Расчитываем вероятность выбора карты одной масти по формуле классической вероятности: вероятность = 13 / 52 = 0.25 (или 25%).
Таким образом, шанс выбрать карту одной масти из стандартной колоды равен 0.25 или 25%.
Использование формулы относительной вероятности

Формула относительной вероятности выглядит следующим образом:
P(A|B) = P(A ∩ B) / P(B),
где P(A|B) обозначает вероятность события A при условии, что произошло событие B; P(A ∩ B) обозначает вероятность одновременного наступления событий A и B; P(B) обозначает вероятность события B.
Для иллюстрации работы этой формулы, предположим, что мы хотим выяснить вероятность того, что у случайно выбранного человека будет iPhone при условии, что у него есть смартфон. У нас есть следующие данные: из 100 случайных людей 70 имеют смартфон, а 30 из них имеют iPhone.
Теперь мы можем посчитать вероятность, используя формулу относительной вероятности:
P(iPhone|смартфон) = P(iPhone ∩ смартфон) / P(смартфон) = 30/100 / 70/100 = 3/7
Таким образом, вероятность того, что у случайно выбранного человека будет iPhone при условии, что у него есть смартфон, составляет 3/7.
Использование формулы относительной вероятности помогает нам более точно определить вероятность события, учитывая другие факторы или условия. Это важный инструмент в статистике, и его использование может помочь нам принимать более информированные решения и делать точные предсказания.
Вычисление вероятности событий по формуле условной вероятности

Формула условной вероятности имеет вид:
P(A|B) = P(A ∩ B) / P(B)
где P(A|B) - условная вероятность события A при условии, что событие B произошло, P(A ∩ B) - вероятность наступления события A и B одновременно, P(B) - вероятность наступления события B.
Для того чтобы вычислить условную вероятность, необходимо знать значения P(A ∩ B) и P(B), которые можно получить на основе имеющихся данных или же на основе предположений.
Пример вычисления условной вероятности:
Предположим, что у нас есть информация о том, что у определенной группы людей был проведен определенный медицинский тест. Событие А - человек болен, событие В - тест показал положительный результат. Мы хотим вычислить вероятность того, что человек болен, при условии, что тест показал положительный результат.
На основе имеющихся данных мы можем определить вероятность наступления событий P(A ∩ B) и P(B). Используя формулу условной вероятности, мы можем вычислить P(A|B).
Применение формулы совместной вероятности для нахождения вероятности нескольких событий

Для нахождения вероятности нескольких событий одновременно можно использовать формулу совместной вероятности. Эта формула позволяет определить вероятность наступления двух или более событий, при условии, что вероятности каждого события уже известны.
Формула совместной вероятности имеет следующий вид:
P(A и B) = P(A) * P(B|A)
Где:
- P(A и B) - вероятность наступления событий A и B одновременно
- P(A) - вероятность наступления события A
- P(B|A) - вероятность наступления события B при условии, что событие A уже произошло
Для использования этой формулы необходимо знать вероятности каждого события и условную вероятность. Условная вероятность определяется как отношение вероятности наступления обоих событий одновременно к вероятности наступления первого события:
P(B|A) = P(A и B)/P(A)
Применение формулы совместной вероятности может быть полезным, например, при расчете вероятности получения определенной комбинации результатов в игре или при оценке вероятности одновременного наступления двух независимых событий в реальной жизни.
Таким образом, формула совместной вероятности позволяет находить вероятность нескольких событий, исходя из уже известных вероятностей каждого события и условной вероятности.