Гиперболы являются одним из самых интересных объектов в геометрии. Их красивые, асимметричные кривые привлекают внимание исследователей уже на протяжении многих столетий. Одним из ключевых свойств гиперболы является наличие вершин, которые служат важными точками определения и анализа кривой.
Когда гипербола имеет центр смещения, процесс нахождения вершин становится немного сложнее, но все еще выполнимым. Центр смещения - это точка, в которой оси симметрии гиперболы не пересекаются. В этой статье мы рассмотрим, как найти вершины гиперболы с центром смещения, чтобы помочь вам лучше понять и визуализировать эту уникальную кривую.
Для начала, давайте вспомним, что такое гипербола с центром смещения. Гипербола - это кривая, определяемая разностью расстояний от любой точки на кривой до двух фиксированных точек, называемых фокусами. Однако, при наличии центра смещения, оси и фокусы гиперболы сдвигаются относительно исходного положения.
Определение гиперболы с центром смещения

Чтобы определить гиперболу с центром смещения, необходимо знать следующие параметры:
- Центр гиперболы - точка, от которой отсчитывается смещение;
- Расстояние от центра до фокусов - обозначается символом c и определяет, насколько глубоко гипербола изогнута;
- Расстояние от центра до вершин - обозначается символом a и определяет длину оси гиперболы;
- Характеристика гиперболы - это отношение c/a, которое определяет степень сжатия или растяжения гиперболы.
Координаты вершин гиперболы с центром смещения могут быть найдены с помощью формул:
x = h ± a
y = k
Где (h, k) - координаты центра гиперболы, a - расстояние от центра до вершин.
Определение гиперболы с центром смещения является важным шагом при выполнении задач по аналитической геометрии и применяется в различных областях, включая физику, инженерию и экономику.
Теория о вершинах гиперболы
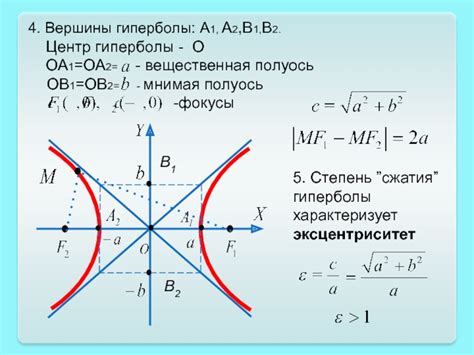
Для гиперболы с уравнением x^2/a^2 - y^2/b^2 = 1 вершины находятся на главных осях кривой. Ось x называется главной осью смещения, и расстояние от центра до вершин по этой оси равно a. Ось y называется второстепенной осью смещения, и расстояние от центра до вершин по этой оси равно b.
Если гипербола имеет уравнение y^2/a^2 - x^2/b^2 = 1, то все то же самое применимо, но оси x и y меняются местами.
Вершины гиперболы имеют большое значение для анализа графика и нахождения фокусов и асимптот. Они помогают понять форму и ориентацию кривой, а также определить ее характеристики и свойства.
Шаги для нахождения вершин гиперболы с центром смещения
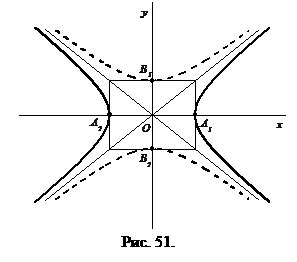
Шаг 1: Запишите уравнение гиперболы в стандартной форме, которое выглядит следующим образом:
(x - h)² / a² - (y - k)² / b² = 1,
где (h, k) - координаты центра гиперболы, а a и b - длины полуосей.
Шаг 2: Сравните данное уравнение с уравнением стандартной, непереведенной гиперболы:
x² / a² - y² / b² = 1
При сравнении вы должны заметить, что переменные x и y в уравнении для смещенной гиперболы заменены на (x - h) и (y - k), соответственно.
Шаг 3: Изучите знаки a² и b² в уравнении смещенной гиперболы:
- Если a² положительно (a² > 0), то полуоси гиперболы расположены вдоль осей x и y и открываются влево и вправо.
- Если a² отрицательно (a² < 0), то полуоси гиперболы находятся вдоль оси y и открываются вверх и вниз.
Шаг 4: Выразите центр смещения (h, k) из уравнения смещенной гиперболы.
- Для вычисления координаты h замените x на 0 и решите уравнение для y, используя значение b и k из уравнения смещенной гиперболы.
- Для вычисления координаты k замените y на 0 и решите уравнение для x, используя значение a и h из уравнения смещенной гиперболы.
Шаг 5: Вычислите вершины гиперболы смещения с помощью координат центра смещения и длин полуосей.
- Для гиперболы, открывающейся влево и вправо, вершины будут находиться на расстоянии a от центра смещения вдоль оси x.
- Для гиперболы, открывающейся вверх и вниз, вершины будут находиться на расстоянии b от центра смещения вдоль оси y.
Не забудьте проверить свои вычисления и уравнение, чтобы убедиться, что они верны. Теперь вы знаете, как найти вершины гиперболы с центром смещения!
Пример решения задачи

Для того чтобы найти вершины гиперболы с центром смещения, следуйте следующим шагам:
- Шаг 1: Запишите уравнение гиперболы в канонической форме. Оно должно иметь вид (x - h)²/a² - (y - k)²/b² = 1 или (y - k)²/b² - (x - h)²/a² = 1, где (h, k) - координаты центра гиперболы, a - расстояние от центра гиперболы до фокусов, b - расстояние от центра гиперболы до вершин.
- Шаг 2: Определите значения a, b и (h, k) из уравнения гиперболы.
- Шаг 3: Используя значения a, b и (h, k), найдите координаты вершин гиперболы.
- Шаг 4: Проверьте полученные координаты, подставив их в уравнение гиперболы и убедившись, что оно выполняется.
Например, пусть дано уравнение гиперболы (x - 2)²/9 - (y + 1)²/16 = 1.
Из этого уравнения можно выделить следующие значения:
Центр смещения: (h, k) = (2, -1)
Расстояние до фокусов: a = 3
Расстояние до вершин: b = 4
Используя эти значения, можно найти координаты вершин гиперболы:
Вершина 1: (2, -5)
Вершина 2: (2, 3)
Проверим, что полученные координаты удовлетворяют уравнению гиперболы:
Для вершины 1: (2 - 2)²/9 - (-5 + 1)²/16 = 1
Для вершины 2: (2 - 2)²/9 - (3 + 1)²/16 = 1
Оба выражения равны 1, поэтому координаты вершин гиперболы (2, -5) и (2, 3) являются верными.