Вписанный угол - это угол, вершина которого лежит на окружности, а стороны проходят через точки окружности. Такой угол является важным элементом в геометрии и часто встречается в различных задачах.
Найти вписанный угол можно с помощью нескольких шагов:
Шаг 1: Найдите дугу, которая соответствует данному углу. Для этого нужно найти точки пересечения сторон угла с окружностью.
Шаг 2: Найдите центр окружности. Он находится на пересечении диагоналей, проведенных через центр угла и центр окружности.
Шаг 3: Найдите радиус окружности. Он равен расстоянию от центра до любой точки окружности.
Шаг 4: Рассчитайте длину дуги, соответствующей углу. Для этого нужно умножить радиус на величину угла в радианах.
Шаг 5: Рассчитайте длину дуги, соответствующей всей окружности. Она равна произведению радиуса на 2π.
Шаг 6: Рассчитайте вписанный угол. Для этого нужно разделить длину дуги, соответствующей углу, на длину дуги, соответствующей всей окружности, и умножить на 360 градусов.
Используя эти шаги, вы без труда сможете найти вписанный угол в окружности без дуги и решить геометрические задачи, связанные с ним. Удачи в изучении геометрии!
Как найти вписанный угол в окружности без дуги?

Вписанный угол в окружности без дуги представляет собой угол, вершина которого лежит на окружности, а его стороны проходят через точки пересечения окружности с хордой или касательной. Нахождение вписанного угла в окружности без дуги может быть полезным при решении задач геометрии или вычислении геометрических параметров фигур.
Для нахождения вписанного угла в окружности без дуги, следуйте инструкциям:
Шаг 1: Найдите хорду или касательную, на которой лежит вписанный угол. Постройте данную линию и отметьте точки пересечения с окружностью.
Шаг 2: Измерьте угол между отрезками, соединяющими центр окружности с каждой из точек пересечения хорды или касательной с окружностью. Этот угол будет половиной искомого вписанного угла.
Шаг 3: Удвойте измеренный угол, чтобы найти вписанный угол в окружности без дуги. Это можно сделать с помощью заданного геометрического инструмента или с помощью математической операции умножения на 2.
Примечание: Чтобы найти вписанный угол в окружности с дугой, необходимо измерить длину дуги и вычислить соответствующий угол, используя радиус окружности.
Теперь, имея пошаговую инструкцию, вы можете легко находить вписанные углы в окружности без дуги и использовать их для решения задач геометрии.
Шаг 1: Начните с определения окружности

1. Центр окружности: Центр окружности - это точка, которая находится в середине окружности и от которой все точки окружности находятся на одинаковом расстоянии. Чтобы найти центр окружности, можно использовать геометрические построения или известные координаты центра.
2. Радиус окружности: Радиус окружности - это расстояние от центра окружности до любой точки на окружности. Радиус можно найти, зная длину отрезка, соединяющего центр окружности с точкой на окружности.
Определение окружности является первым шагом в нахождении вписанного угла в окружности без дуги. Имея определенную окружность, можно переходить к последующим шагам для нахождения вписанного угла.
Шаг 2: Определите радиус окружности
Вариант 1: Если вам даны координаты центра окружности и любой точки на окружности, вы можете использовать формулу расстояния между двумя точками в координатной плоскости, чтобы найти длину радиуса. Формула выглядит следующим образом:
| Радиус | = | √[(x2 - x1)² + (y2 - y1)²] |
Где (x1, y1) - координаты центра окружности, (x2, y2) - координаты точки на окружности.
Вариант 2: Если вам дана длина диаметра окружности, вы можете найти радиус, разделив длину диаметра пополам. Формула будет такой:
| Радиус | = | Диаметр / 2 |
Зная радиус окружности, вы можете продолжить к следующему шагу и найти вписанный угол в окружности без дуги.
Шаг 3: Найдите центр окружности
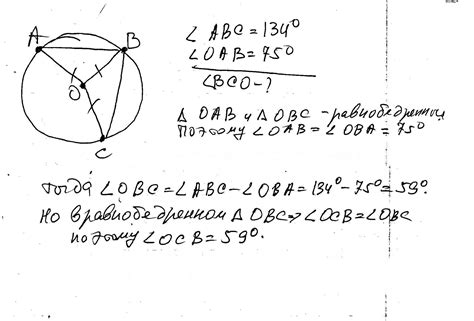
Чтобы найти центр окружности, вам понадобится помощь рисунка. Исходя из предоставленной информации, нарисуйте на листе бумаги окружность, используя циркуль или другие подходящие инструменты.
Затем поставьте точку A на окружности. Она должна быть не произвольной, а той, относительно которой вы знаете угол. От точки A проведите диаметр перпендикулярно углу BAC.
Проведите также диаметр, проходящий через любую другую точку на окружности и являющийся его максимального длины. Этот диаметр должен касаться угла BAC.
Точка пересечения обоих диаметров станет центром окружности. Отметьте ее на своем рисунке. Вы обнаружите, что все четыре отрезка от центра окружности до различных точек на окружности являются равными. Это означает, что вам не нужно знать точные значения радиуса для решения задачи.
Шаг 4: Измерьте угол, образованный хордой и радиусом
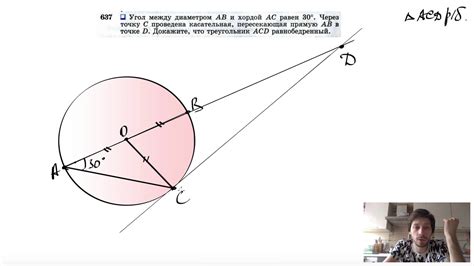
Для определения вписанного угла, образованного хордой и радиусом, вам необходимо измерить угол между ними. Для этого выполните следующие действия:
- Установите центр окружности с помощью циркуля или другого инструмента, который позволяет провести радиус.
- Проведите радиус от центра окружности к одной из точек хорды.
- Измерьте угол, образованный радиусом и хордой с помощью угломера или протрактора. Запишите этот угол.
Теперь у вас есть значение вписанного угла, образованного хордой и радиусом. Вы можете использовать это значение для решения задач, связанных с окружностью и ее вписанными углами.