Вписанный угол в треугольнике – это угол, вершина которого лежит на окружности, вписанной в данный треугольник. Этот угол имеет особую геометрическую связь с точками касания окружности с сторонами треугольника. Найти вписанный угол треугольника можно, используя некоторые известные свойства треугольника и окружности.
Для нахождения вписанного угла треугольника необходимо знать следующую основную формулу: мироугольная формула. Время от времени вам может понадобиться находить вписанный угол треугольника для решения математических задач, в которых углы и окружности играют важную роль.
Зная формулу, вы сможете с легкостью находить вписанный угол треугольника. Он позволит вам решать задачи на уровне школьной программы и вплоть до олимпиадного уровня. Значит, научившись находить вписанный угол треугольника, вы значительно расширите свои математические и аналитические навыки.
Методы нахождения вписанного угла треугольника
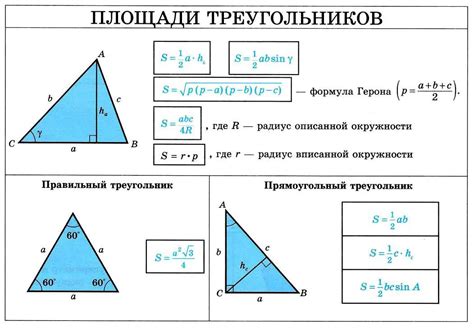
Существует несколько методов для нахождения вписанного угла треугольника:
1. Теорема о вписанном угле: Если угол треугольника опирается на дугу окружности, то его величина равна половине величины соответствующей центральной округлостной дуги.
2. Острый угол: Если треугольник остроугольный (все его углы острые), то вписанный угол будет меньше 90 градусов.
3. Тупой угол: Если треугольник тупоугольный (имеет хотя бы один тупой угол), то два вписанных угла будут больше 90 градусов.
4. Центральный угол: Если угол треугольника опирается на центральную округлостную дугу, то его величина равна удвоенному величине соответствующего вписанного угла.
Использование данных методов позволяет находить вписанный угол треугольника и применять его в решении различных геометрических задач, таких как построение фигур, нахождение площади треугольника и другие.
Формулы для вычисления вписанного угла треугольника
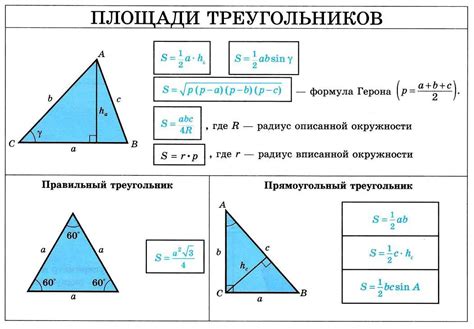
Для вычисления вписанного угла треугольника можно использовать следующие формулы:
- Если известны длины сторон треугольника (a, b, c), тогда вписанный угол (α) можно вычислить по формуле: α = 2 * arcsin(sqrt((s*(s-a)*(s-b)*(s-c)) / (abc))), где s = (a + b + c) / 2 - полупериметр треугольника.
- Если известны длины двух сторон треугольника (a, b) и величина вписанного угла (α), тогда длину третьей стороны (c) можно вычислить по формуле: c = sqrt(a^2 + b^2 - 2ab*cos(α)).
- Если известны длины двух сторон треугольника (a, b) и величина вписанного угла (α), тогда площадь треугольника (S) можно вычислить по формуле: S = 0.5 * a * b * sin(α).
Эти формулы можно использовать для вычисления вписанного угла треугольника в различных задачах геометрии и тригонометрии.
Примеры решения задач по нахождению вписанного угла треугольника
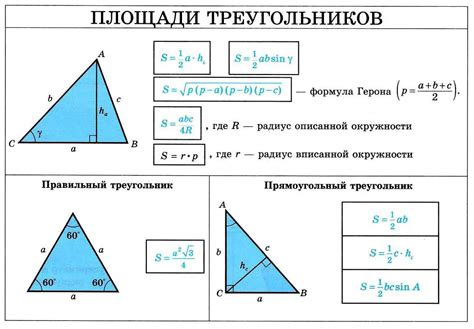
Пример 1:
Дано: треугольник ABC, вписанный в окружность с центром O.
Задача: найти меру угла ABC.
Решение:
1. С помощью известной формулы для вписанного угла найдем меру дуги AC: мера дуги AC = 2 * меру угла ABC.
2. Известно, что мера дуги AC равна 120 градусам (так как она составляет треть всей окружности).
3. Подставим значение меры дуги в формулу: 120 = 2 * меру угла ABC.
4. Разделим обе части уравнения на 2: мера угла ABC = 60 градусов.
Ответ: мера угла ABC равна 60 градусам.
Пример 2:
Дано: треугольник DEF, вписанный в окружность с центром O.
Задача: найти меру угла DEF.
Решение:
1. С помощью известной формулы для вписанного угла найдем меру дуги EF: мера дуги EF = 2 * меру угла DEF.
2. Известно, что мера дуги EF равна 90 градусам (так как она составляет четверть всей окружности).
3. Подставим значение меры дуги в формулу: 90 = 2 * меру угла DEF.
4. Разделим обе части уравнения на 2: мера угла DEF = 45 градусов.
Ответ: мера угла DEF равна 45 градусам.
Пример 3:
Дано: треугольник GHI, вписанный в окружность с центром O.
Задача: найти меру угла GHI.
Решение:
1. С помощью известной формулы для вписанного угла найдем меру дуги GH: мера дуги GH = 2 * меру угла GHI.
2. Известно, что мера дуги GH равна 60 градусам (так как она составляет треть всей окружности).
3. Подставим значение меры дуги в формулу: 60 = 2 * меру угла GHI.
4. Разделим обе части уравнения на 2: мера угла GHI = 30 градусов.
Ответ: мера угла GHI равна 30 градусам.