Высота через радиус вписанной окружности – это одно из важнейших геометрических параметров треугольника. Она позволяет определить расстояние от вершины треугольника до основания, проходящее через центр вписанной окружности. Этот параметр может быть полезен при решении разнообразных задач в геометрии и алгебре, поэтому владение методом нахождения высоты через радиус вписанной окружности может существенно облегчить жизнь как ученику, так и учителю.
Для начала, давайте рассмотрим, что такое вписанная окружность и как она связана с высотой треугольника. Вписанная окружность – это окружность, которая касается всех трех сторон треугольника. Важным свойством такой окружности является то, что линия, соединяющая вершину треугольника с центром вписанной окружности, перпендикулярна к стороне треугольника.
Теперь, когда мы установили связь вписанной окружности с высотой треугольника, давайте перейдем к методу нахождения высоты через радиус вписанной окружности. Воспользуемся теоремой Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В нашем случае гипотенуза – это радиус вписанной окружности, а катетами являются высота и отрезок, соединяющий основание треугольника с центром вписанной окружности. Подставив известные значения в теорему Пифагора, мы сможем найти неизвестную высоту.
Определение вписанной окружности
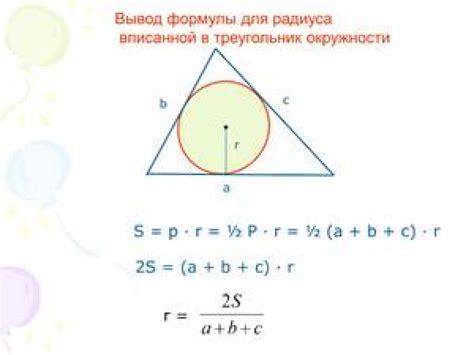
Определить вписанную окружность можно с помощью известных данных о треугольнике. Если в треугольнике известны длины всех трех сторон, то радиус вписанной окружности можно вычислить по формуле:
- Вычислите полупериметр треугольника: p = (a + b + c) / 2
- Вычислите площадь треугольника: S = √(p(p - a)(p - b)(p - c))
- Вычислите радиус вписанной окружности: r = S / p
Где a, b и c - длины сторон треугольника.
Зная радиус вписанной окружности и одну из сторон треугольника, можно вычислить высоту, опускаемую на эту сторону с помощью теоремы Пифагора.
Уникальность вписанной окружности заключается в том, что она касается всех трех сторон треугольника в одной и той же точке и является единственной окружностью, которая удовлетворяет этому условию для данного треугольника.
Связь радиуса вписанной окружности с высотой треугольника
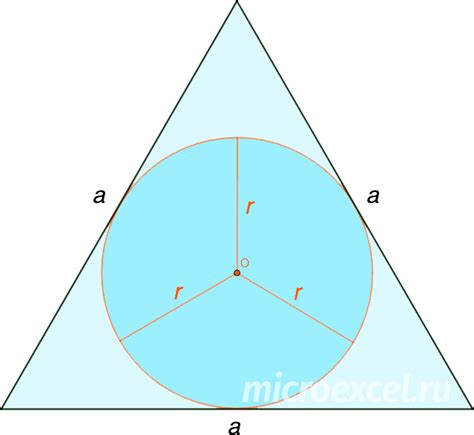
Пусть радиус вписанной окружности равен R, а высота треугольника, проведенная к основанию, равна h.
Тогда, согласно формуле площади треугольника S = 1/2 * a * h, где a – длина основания треугольника, имеем:
S = 1/2 * a * h = 1/2 * (2R) * h = R * h
Таким образом, площадь треугольника равна произведению радиуса вписанной окружности и высоты треугольника, умноженных друг на друга.
Зная радиус вписанной окружности и высоту треугольника, мы можем выразить одну величину через другую:
h = S / R
R = S / h
Таким образом, высота треугольника связана с радиусом вписанной окружности следующим образом: высота равна площади треугольника, деленной на радиус.
Вычисление высоты через радиус вписанной окружности
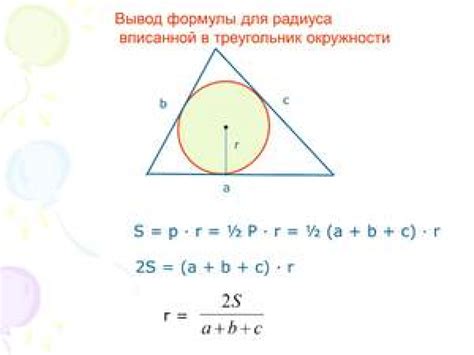
Высоту треугольника можно вычислить с использованием радиуса вписанной окружности, используя следующий алгоритм:
Шаг 1: Найдите площадь треугольника, используя формулу Герона или другие известные способы вычисления площади треугольника.
Шаг 2: Найдите длину основания треугольника, которая является суммой сторон треугольника.
Шаг 3: Используя формулу площади треугольника, найдите высоту треугольника по формуле:
высота = 2 * площадь / основание
Шаг 4: Если изначально дан радиус вписанной окружности треугольника, найдите площадь треугольника через радиус по формуле:
площадь = радиус * полупериметр
После этого можно приступать к выполнению шагов 2 и 3.
Вычисление высоты треугольника через радиус вписанной окружности может быть полезным в различных задачах, связанных с геометрией и строительством.
Пример решения задачи на практике

Допустим, что у нас есть треугольник ABC, в котором вписана окружность. Известны радиус вписанной окружности (r) и сторона треугольника (a).
1. Найдем площадь треугольника ABC по формуле S = a * h / 2, где h - высота треугольника.
2. Площадь треугольника также можно выразить через радиус вписанной окружности: S = (a * r) / 2. Подставив это выражение в формулу площади треугольника, получим a * h / 2 = (a * r) / 2.
3. Пользуясь этим равенством, найдем высоту треугольника: h = (a * r) / a = r.
4. Таким образом, высота треугольника равна радиусу вписанной окружности.
| Название переменной | Описание |
|---|---|
| r | Радиус вписанной окружности |
| a | Сторона треугольника |
| h | Высота треугольника |