Высота прямоугольного треугольника является одной из важных характеристик этой геометрической фигуры. Она позволяет нам определить длину отрезка, проведенного от вершины прямого угла до основания треугольника. Знание высоты треугольника может быть полезным в различных областях, включая строительство, архитектуру, геодезию и многие другие.
Так как треугольники являются одной из основных фигур в геометрии, владение методами расчета их параметров является неотъемлемой частью математического образования. Нахождение высоты прямоугольного треугольника по основанию и углу может показаться сложной задачей, но на самом деле это достаточно просто.
В этой статье мы рассмотрим, как найти высоту прямоугольного треугольника, используя основание и угол. Мы предоставим несколько примеров для лучшего понимания и подробно разберем каждый шаг расчета. Вы узнаете, как применить эти знания на практике и получить точный результат.
Определение прямоугольного треугольника

Основной параметр прямоугольного треугольника - это его высота. Высота прямоугольного треугольника - это отрезок, проведенный от вершины прямого угла до основания, перпендикулярно к основанию.
Высота прямоугольного треугольника имеет особое значение, поскольку она является частью теоремы Пифагора, которая утверждает, что квадрат длины гипотенузы (стороны, противоположной прямому углу) равен сумме квадратов длин катетов (других двух сторон). В случае прямоугольного треугольника, длина высоты может быть использована для вычисления длин катетов и гипотенузы.
Чтобы найти высоту прямоугольного треугольника, необходимо знать длину одного из катетов (основание) и угол, противолежащий этому катету. Поэтому для вычисления высоты прямоугольного треугольника требуется знание основания и угла.
Формула высоты прямоугольного треугольника
Формула для высоты прямоугольного треугольника имеет следующий вид:
h = син(α) * b
где:
- h - высота прямоугольного треугольника;
- син(α) - значение синуса угла при основании треугольника;
- b - длина основания.
Чтобы использовать эту формулу, измерьте или определите длину основания и угол при его основании. Затем подставьте эти значения в формулу и произведите вычисления. Результатом будет высота прямоугольного треугольника.
Например, пусть длина основания треугольника равна 6 единицам, а угол α составляет 30 градусов. Для вычисления высоты, поместим значения в формулу:
h = син(30°) * 6 = 0.5 * 6 = 3
Таким образом, высота прямоугольного треугольника составляет 3 единицы.
Эта формула позволяет эффективно вычислить высоту прямоугольного треугольника, основываясь на известных значениях длины основания и угла при его основании.
Выражение высоты через основание и угол
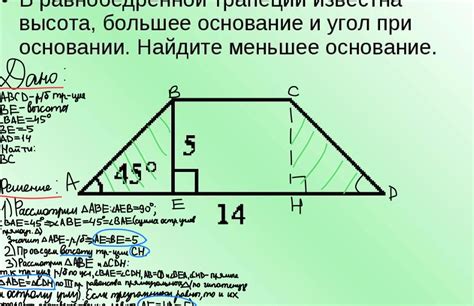
Для этого используется формула:
h = a * sin(α)
где h - высота треугольника, a - основание треугольника, α - угол между основанием и высотой.
Например, если у нас есть прямоугольный треугольник, где основание равно 5 и угол между основанием и высотой равен 30 градусам, мы можем найти высоту треугольника по формуле:
h = 5 * sin(30°) = 5 * 0.5 = 2.5
Таким образом, высота треугольника равна 2.5 единицы длины.
Используя данную формулу, можно рассчитать высоту прямоугольного треугольника, если известны значения основания и угла между основанием и высотой.
Пример 1: Расчет высоты прямоугольного треугольника
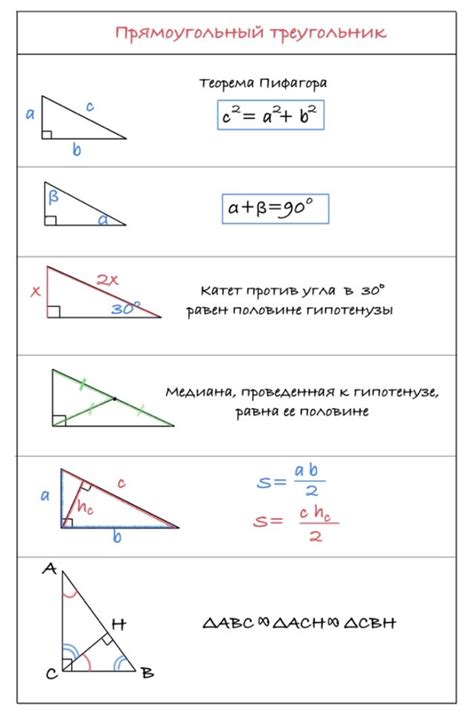
Допустим, у нас есть прямоугольный треугольник с заданным основанием и углом при основании. Мы хотим найти его высоту.
Для начала, нам понадобятся следующие данные:
- длина основания треугольника, обозначаемая буквой a;
- угол, образованный основанием и гипотенузой треугольника, обозначаемый буквой α.
Используя тригонометрические функции, мы можем выразить высоту треугольника через заданные данные:
h = a * sin(α)
Например, рассмотрим треугольник с основанием длиной 5 единиц и углом α равным 30 градусам. Чтобы найти высоту треугольника, мы можем подставить данные в формулу:
h = 5 * sin(30°)
h = 5 * 0.5
h = 2.5
Таким образом, высота прямоугольного треугольника с основанием длиной 5 единиц и углом α равным 30 градусам равна 2.5 единицам.
Пример 2: Расчет высоты прямоугольного треугольника
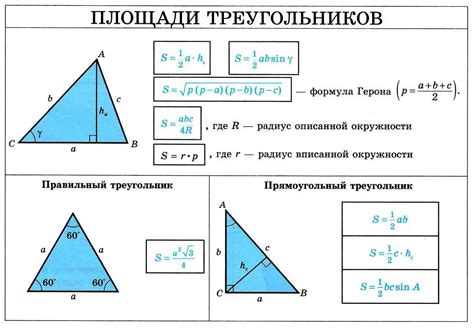
Допустим, у нас есть прямоугольный треугольник со сторонами a = 5 и b = 12, а угол между ними равен 90 градусов.
Чтобы найти высоту треугольника, мы можем использовать формулу:
- Рассчитаем площадь треугольника с помощью формулы: площадь = (основание * высота) / 2
- Подставим известные значения: площадь = (5 * h) / 2
- Так как у нас уже есть значение одной стороны (5), мы можем найти высоту, используя формулу площади: h = (2 * площадь) / основание
- Подставим в формулу значения: h = (2 * площадь) / основание = (2 * площадь) / 5 = (2 * (5 * 12) / 2) / 5 = 12 / 5 = 2.4
Таким образом, высота прямоугольного треугольника равна 2.4 единицы длины.
Несколько полезных советов при работе с высотами треугольников
Когда требуется найти высоту прямоугольного треугольника, существуют несколько полезных советов, которые следует учесть:
- Используйте основание треугольника и соответствующий ему угол, чтобы определить высоту. Для этого можно воспользоваться тригонометрическим соотношением: высота равна произведению синуса угла на длину основания.
- Убедитесь, что используете правильную систему измерения для длины основания. Если основание представлено в сантиметрах, угол должен быть задан в радианах.
- Если вам известны длина гипотенузы и один из катетов прямоугольного треугольника, чтобы найти второй катет, можно воспользоваться теоремой Пифагора. Затем высоту можно найти, используя любой катет и соответствующий угол треугольника.
- Не забывайте проверять свои вычисления с помощью геометрических свойств треугольников. Высота должна быть перпендикулярна основанию и проходить через вершину противолежащего угла.
Следуя этим советам, вы сможете легко и точно найти высоту прямоугольного треугольника, используя известные данные. Не забывайте проводить проверку своих вычислений и обращаться к геометрическим свойствам треугольников для достоверности результата.