Равнобедренный треугольник - это фигура, у которой две стороны и два угла равны. Обычно для определения высоты равнобедренного треугольника требуется знание длины его основания. Однако, иногда может возникнуть необходимость найти высоту, когда длина основания неизвестна. В таких случаях можно использовать различные подходы и формулы для определения данной величины. В этой статье мы рассмотрим несколько способов решения данной задачи.
Один из способов нахождения высоты равнобедренного треугольника без основания основан на применении теоремы Пифагора. Для этого можно использовать правильный треугольник, в котором стороны имеют равную длину. Зная длину стороны треугольника, можно найти ее высоту, применив теорему Пифагора.
Еще один метод заключается в использовании свойств равнобедренного треугольника. Например, высота треугольника, проведенная из вершины до основания, делит его на два равнобедренных треугольника и прямоугольный треугольник. Используя эти свойства, можно составить систему уравнений и решить ее для нахождения высоты.
Высота равнобедренного треугольника: как найти
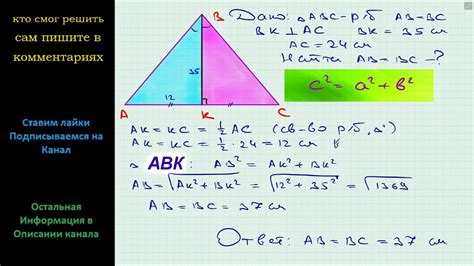
Для того чтобы найти высоту равнобедренного треугольника, можно использовать теорему Пифагора. Зная длину основания и длину стороны треугольника, можно вычислить высоту.
Пусть a - длина основания, b - длина стороны треугольника. Высоту треугольника можно найти по формуле:
h = √(b² - a²/4)
Применяя формулу, получаем значения высоты равнобедренного треугольника. Найденная высота будет перпендикулярна основанию и проходит через вершину треугольника.
Определение высоты

Один из методов - использование теоремы Пифагора. Если известны длины сторон равнобедренного треугольника, то длина высоты может быть вычислена с помощью следующей формулы:
h = sqrt(a2 - (b/2)2)
где h - высота, a - длина основания, b - длина одной из боковых сторон.
Если известны углы треугольника, то можно использовать тригонометрические соотношения для нахождения высоты. Например, если известны угол между основанием и одной из боковых сторон (α), угол между основанием и высотой (β), и длина основания (a), то длина высоты (h) может быть найдена по формуле:
h = a * tan(β)
где tan - функция тангенса.
Также можно использовать свойство равнобедренного треугольника - основание и высоту делятся пополам. Если известна длина основания (a), то высота (h) будет равна:
h = a/2
Выбор метода для определения высоты равнобедренного треугольника зависит от доступной информации и предпочтений. Важно помнить, что при совершении вычислений необходимо быть внимательным и точным.
Формула высоты в зависимости от стороны

Для вычисления высоты равнобедренного треугольника, когда известна длина одной из сторон, можно использовать специальную формулу. Эта формула позволяет найти высоту треугольника без необходимости знания длины основания.
Формула для вычисления высоты равнобедренного треугольника выглядит следующим образом:
h = √(a^2 - (b^2 / 4))
где:
- h - высота треугольника
- a - длина стороны треугольника
- b - длина основания треугольника
Используя данную формулу, можно легко получить высоту равнобедренного треугольника, зная длину одной из его сторон. Это очень удобно, когда основание треугольника неизвестно, но есть информация о его сторонах.
Как найти высоту без основания
- Найдите длину одного из равных сторон треугольника. Для этого можно использовать теорему Пифагора или известные данные о треугольнике.
- Разделите значение стороны треугольника на 2, чтобы найти половину основания.
- Используя полученное значение половины основания, используйте теорему Пифагора, чтобы найти длину высоты.
Если основание треугольника неизвестно, но известны стороны, можно использовать другую формулу для нахождения высоты.
- Найдите площадь треугольника, используя формулу герона или другой способ.
- Разделите удвоенную площадь треугольника на длину одной из сторон, чтобы найти длину высоты.
Обратите внимание, что для нахождения высоты без основания требуется знание длин сторон или площади треугольника. Если известны только углы треугольника или другие данные, такие как радиус вписанной окружности, может потребоваться использование других алгоритмов или формул.
Пример решения задачи

Для нахождения высоты равнобедренного треугольника без основания можно использовать свойство подобности треугольников.
Пусть дан равнобедренный треугольник ABC, где AB = AC и высота треугольника BD. Треугольники ABC и ABD подобны, так как у них одинаковый угол при вершине A и общий угол B.
Таким образом, можно записать пропорцию:
AB/BD = AC/AD
Так как AB = AC, пропорция упрощается:
1/BD = 1/AD
Отсюда следует, что BD = AD. Это означает, что высота равнобедренного треугольника равна половине стороны, проведенной из вершины до основания.
Таким образом, чтобы найти высоту треугольника, нужно найти половину длины основания и это будет значение высоты.