Высота равнобедренного треугольника – это линия, проведенная из вершины треугольника перпендикулярно к основанию. Знание высоты треугольника может быть полезным при решении различных геометрических задач. В данной статье мы рассмотрим несколько методов расчета высоты равнобедренного треугольника и приведем примеры, демонстрирующие их применение.

Первый метод основан на использовании теоремы Пифагора. Для этого необходимо знать длину основания треугольника и длину его боковой стороны. Сначала найдем половину длины основания, поделив ее на 2. Затем найдем длину высоты треугольника по формуле: высота к квадрату равна квадрату боковой стороны минус квадрат половины основания. Полученный результат извлеките из подкоренного выражения, и вы получите длину высоты.

Второй метод основан на использовании теоремы косинусов. Для этого необходимо знать длину основания треугольника и величину одного из его углов. Сначала найдем значение косинуса половины угла, используя формулу: косинус половины угла равен квадрату половины основания, деленного на сумму квадратов половины основания и квадрата боковой стороны. Затем найдем длину высоты треугольника, умножив косинус половины угла на длину основания.

Приведенные методы позволяют найти высоту равнобедренного треугольника к основанию и решать с их помощью различные задачи. Рассмотрим пример. Пусть у нас есть равнобедренный треугольник с основанием длиной 10 см и боковой стороной длиной 8 см. По первому методу найдем длину высоты: половина основания равна 5 см, поэтому по формуле получим значение в подкоренном выражении: 8^2 - 5^2 = 39. Извлекаем корень, получаем 6,24 см. По второму методу значение косинуса половины угла равно 5^2 / (5^2 + 4^2) = 0,69, умножаем на длину основания 10 см и получаем 6,90 см. Таким образом, высота равнобедренного треугольника к основанию составляет около 6,24 – 6,90 см.

Методы нахождения высоты равнобедренного треугольника к основанию

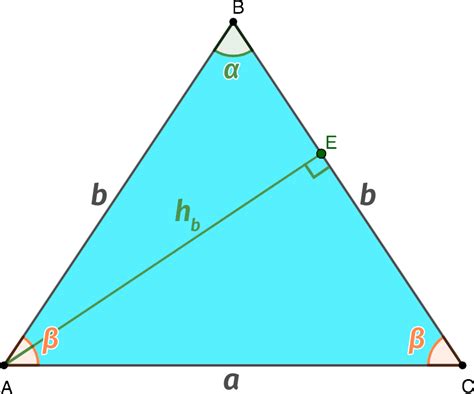
Существует несколько методов нахождения высоты равнобедренного треугольника к основанию.

1. Геометрический метод:

Геометрический метод основан на свойствах равнобедренного треугольника. Если провести высоту из вершины треугольника к основанию, то получится два прямоугольных треугольника, имеющих равные катеты. Поэтому можно использовать теорему Пифагора, чтобы найти высоту как геометрическую среднюю между основанием и половиной его длины.

Формула:

h = √(a^2 - (b/2)^2),

где h - высота равнобедренного треугольника, a - длина основания, b - длина стороны треугольника.

2. Тригонометрический метод:

Тригонометрический метод основан на применении тригонометрических функций для нахождения высоты равнобедренного треугольника. Используя теорему косинусов, можно составить уравнение, которое позволит найти высоту.

Формула:

h = sqrt(b^2 - (a/2)^2),

где h - высота равнобедренного треугольника, a - длина основания, b - длина стороны треугольника.

3. Использование медианы:

Высоту равнобедренного треугольника к основанию можно найти с использованием медианы, опущенной из вершины треугольника. Медиана является отрезком, соединяющим вершину треугольника с серединой основания. Длина медианы равна половине основания. Поэтому можно найти высоту, используя формулу, связывающую медиану и высоту.

Формула:

h = 2 * sqrt(b^2 - (a/4)^2),

где h - высота равнобедренного треугольника, a - длина основания, b - длина стороны треугольника.

Все эти методы позволяют найти высоту равнобедренного треугольника к основанию с использованием различных свойств и теорем геометрии.

Метод 1: Использование теоремы Пифагора

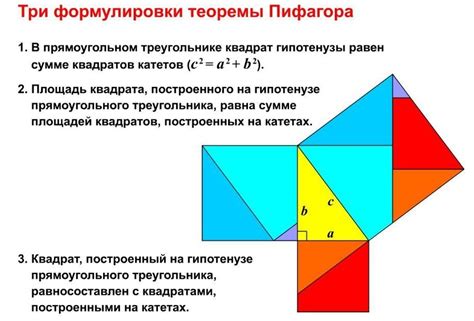
Для нахождения высоты равнобедренного треугольника к его основанию мы можем использовать теорему Пифагора. Для этого нужно построить высоту так, чтобы она перпендикулярно пересекала основание треугольника.

Пусть a - основание треугольника, и h - высота к основанию треугольника.

Используя теорему Пифагора, можем записать:

a² = (h/2)² + h²

Раскроем скобки:

a² = h²/4 + h²

Приведем подобные слагаемые:

a² = 5h²/4

Переместим h² на одну сторону и остальные слагаемые на другую:

4a² = 5h²

Делаем замену под корнем:

h = 2a/√5

Таким образом, мы получили формулу для высоты равнобедренного треугольника к его основанию:

h = 2a/√5

Метод 2: Применение базовой тригонометрии

Для нахождения высоты равнобедренного треугольника к его основанию можно использовать базовые тригонометрические функции. В данном методе нам потребуется знание основных соотношений между сторонами и углами треугольника.

Для начала, разделим равнобедренный треугольник на два прямоугольных треугольника. Рассмотрим один из них. Пусть основание треугольника равно a, а прилежащие к основанию стороны равны b. Высоту треугольника обозначим как h.

Используя теорему Пифагора в прямоугольном треугольнике, получаем следующее соотношение:

a² = h² + (b/2)²

Выразим высоту h через a и b:

h² = a² - (b/2)²

h = √(a² - (b/2)²)

Таким образом, высота равнобедренного треугольника к его основанию находится по формуле, содержащей квадратный корень.

Пример:

Пусть у нас есть равнобедренный треугольник, у которого основание равно 6 см, а сторона равна 8 см. Найдем высоту треугольника.

h = √(8² - (6/2)²)

h = √(64 - 9)

h = √55

h ≈ 7.42 см

Таким образом, высота равнобедренного треугольника с основанием 6 см и стороной 8 см равна примерно 7.42 см.

Метод 3: Вычисление с использованием формулы полупериметра

Высота равнобедренного треугольника к основанию может быть найдена с использованием формулы, основанной на полупериметре треугольника. Для этого необходимо знать длину основания и длину стороны треугольника.

Шаги:

1. Вычислите полупериметр треугольника, сложив длины всех трех сторон и поделив полученную сумму на 2.
2. Используя формулу полупериметра, найдите площадь треугольника.
3. Выразите высоту как отношение площади треугольника к длине основания.

Пример:

Пусть у нас есть равнобедренный треугольник с основанием длиной 8 и стороной треугольника длиной 6. Шаги для вычисления его высоты:

1. Полупериметр треугольника = (6 + 6 + 8) / 2 = 10.
2. Площадь треугольника = √(10 * (10-6) * (10-6) * (10-8)) = 12.
3. Высота треугольника = (2 * 12) / 8 = 3.

Таким образом, высота равнобедренного треугольника к основанию равна 3.

Примеры расчетов высоты равнобедренного треугольника

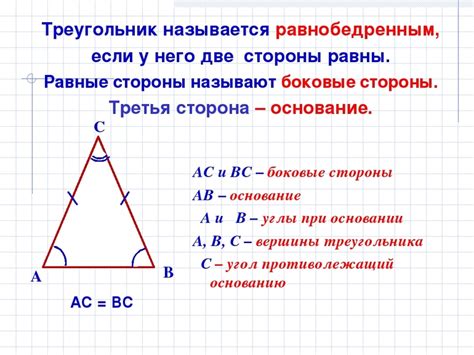
Высота равнобедренного треугольника может быть вычислена с использованием различных методов. Рассмотрим несколько примеров расчетов высоты.

Пример 1: Пусть основание равнобедренного треугольника составляет 10 сантиметров, а его боковая сторона – 8 сантиметров. Чтобы найти высоту, воспользуемся формулой, где высота равна произведению основания и половины длины боковой стороны, деленному на корень из разности единицы и квадрата половины длины боковой стороны:

Высота = (основание * 0.5 * боковая сторона) / √(1 - 0.25)

Подставляя значения в формулу, получаем:

Высота = (10 * 0.5 * 8) / √(1 - 0.25) ≈ 40 / √0.75 ≈ 40 / 0.866 ≈ 46.15 сантиметров

Таким образом, высота равнобедренного треугольника составляет примерно 46.15 сантиметров.

Пример 2: Пусть основание равнобедренного треугольника равно 6 метров, а угол при вершине равен 60 градусов. Для расчета высоты используем формулу, где высота равна произведению косинуса угла при вершине на длину основания:

Высота = косинус(60) * основание

Подставляя значения в формулу, получаем:

Высота = cos(60) * 6 ≈ 0.5 * 6 ≈ 3 метра

Таким образом, высота равнобедренного треугольника равна 3 метрам.

Примеры расчетов высоты равнобедренного треугольника демонстрируют применение различных формул и методов. При знании основных правил геометрии и использовании этих формул можно быстро и точно определить высоту равнобедренного треугольника в различных ситуациях.