Ромб – это геометрическая фигура, которая обладает числом уникальных свойств. Одним из них является равенство длин всех его сторон. Это также означает, что все углы ромба равны между собой. Однако, чтобы полностью описать ромб, нужно знать не только длины его сторон, но и высоту.
Высота ромба – это отрезок, который соединяет противоположные вершины ромба и перпендикулярен его сторонам. Зная диагонали ромба, можно легко найти высоту этой фигуры. Существует несколько способов рассчитать высоту ромба в зависимости от доступных данных.
Самый простой способ:
1. Найдите длины двух диагоналей ромба. Обозначим их как d1 и d2.
2. Рассчитайте площадь ромба по формуле: S = (d1 * d2) / 2.
3. Зная площадь S и длину одной из диагоналей (например, d1), вычислите высоту h по формуле: h = (2 * S) / d1.
Другой способ:
1. Найдите длину одной из диагоналей ромба (например, d1).
2. Рассчитайте длину стороны ромба (a) по формуле: a = (√(d1^2)) / 2.
3. Найдите высоту h, используя формулу: h = 2 * a.
Важно отметить, что диагонали ромба пересекаются под прямым углом, и их половина является основой параллелограмма. Используя эту информацию и зная длину одной из диагоналей, можно вычислить высоту ромба. Эти простые формулы помогут вам рассчитать высоту ромба и использовать ее в геометрических расчетах и построениях.
Задание ромба с заданной диагональю
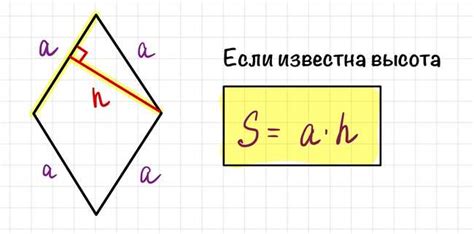
Для задания ромба с заданной диагональю необходимо учесть следующие шаги:
- Найти половину диагонали ромба. Для этого необходимо разделить известную длину диагонали на 2.
- Найти сторону ромба. Для этого используется теорема Пифагора, где сторона ромба является гипотенузой, а половина диагонали - катетом. Необходимо найти катет путем нахождения разницы между длиной диагонали и длиной стороны.
- Найти площадь ромба. Для этого используется формула: площадь = сторона * половина диагонали.
- Найти высоту ромба. Высота ромба - это расстояние между его противоположными сторонами, проходящее через середину диагонали. Высота ромба можно найти, используя формулу: высота = 2 * площадь / сторона.
В результате выполнения этих шагов, задав ромб с заданной диагональю, вы сможете определить его стороны, углы и другие параметры. Эти данные являются важными для выполнения различных геометрических операций и расчетов.
Для удобства и наглядности, можно представить результаты измерений и расчетов в виде таблицы.
| Параметр | Значение |
|---|---|
| Диагональ | заданная длина |
| Половина диагонали | длина диагонали / 2 |
| Сторона | √(длина диагонали^2 - (длина диагонали / 2)^2) |
| Площадь | сторона * половина диагонали |
| Высота | 2 * площадь / сторона |
Зная эти значения, вы сможете успешно задать ромб с заданной диагональю и использовать его в различных геометрических задачах и расчетах.
Важные особенности ромба
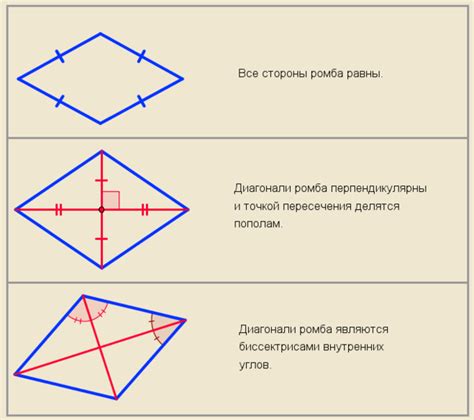
2. Диагонали: В ромбе существуют две диагонали, которые обладают несколькими интересными свойствами. Во-первых, диагонали перпендикулярны друг другу, то есть пересекаются под прямым углом. Во-вторых, каждая диагональ является осью симметрии ромба, что означает, что она делит его на две равные части.
3. Высота: Высота ромба - это линия, пересекающаяся с основанием ромба и образующая с ним прямой угол. Она соединяет противоположные вершины ромба и разделяет его на два равных и подобных треугольника.
4. Формула для вычисления высоты: Для вычисления высоты ромба по заданной диагонали можно использовать формулу:
высота = (диагональ1 * диагональ2) / (2 * сторона)
5. Практическое применение: Ромбы используются в геометрии и в различных областях науки и техники. Они часто встречаются в архитектуре и дизайне, а также используются в различных вычислениях и моделировании.
Определение высоты ромба по заданной диагонали
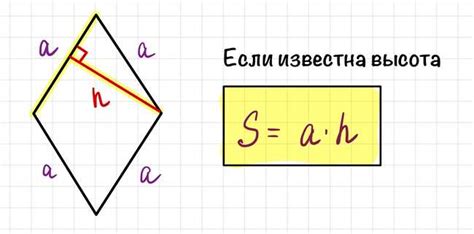
Для определения высоты ромба по заданной диагонали необходимо знать формулу, которая связывает высоту ромба с его диагональю. Формула выглядит следующим образом:
- Если известны длина большой диагонали и длина меньшей диагонали ромба:
- Высота ромба равна произведению длины большой диагонали на длину меньшей диагонали, деленного на модуль разности этих диагоналей:
h = (D1 * D2) / abs(D1 - D2)
- Высота ромба равна произведению длины большой диагонали на корень из двух, деленное на 2:
h = D * sqrt(2) / 2
Эти формулы позволяют определить высоту ромба по заданной диагонали и могут быть использованы при решении различных задач в геометрии. Они основаны на свойствах ромба и позволяют получить точные значения высоты.
Доказательство формулы для вычисления высоты ромба
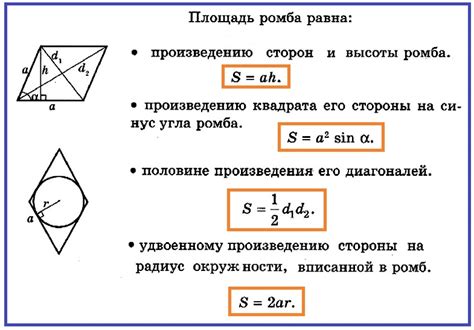
В данном разделе мы рассмотрим доказательство формулы для вычисления высоты ромба. Высоту ромба можно найти, зная любую из его диагоналей и формулу для расчета площади.
Пусть у нас есть ромб со стороной a и диагональю d. Обозначим высоту ромба через h.
Площадь ромба можно выразить двумя способами: через диагонали и через сторону. По формуле для площади ромба через диагонали получаем:
S = (d₁ * d₂) / 2,
где d₁ и d₂ - диагонали ромба.
Так как ромб является параллелограммом, диагонали ромба разделяются пополам и перпендикулярны друг другу. Значит, мы можем представить одну из диагоналей как основание прямоугольника, а другую диагональ как высоту этого прямоугольника. Тогда:
S = d₁ * h,
где h - высота ромба, равная расстоянию между противоположными сторонами.
Теперь мы можем приравнять эти две формулы, так как они оба выражают площадь ромба:
(d₁ * d₂) / 2 = d₁ * h.
Раскрывая скобки, получаем:
d₁ * d₂ = 2 * d₁ * h.
Делим обе части уравнения на d₁, получаем:
d₂ = 2h.
Таким образом, мы получили формулу для вычисления высоты ромба:
h = d₂ / 2.
Примеры решения задачи
Допустим, у нас есть ромб со стороной 4 и диагональю 8. Мы хотим найти высоту этого ромба.
- Используя формулу для высоты ромба, мы можем решить эту задачу следующим образом:
- Делим диагональ пополам: 8 / 2 = 4.
- Подставляем полученное значение в формулу для высоты ромба: высота = (сторона * √(4 - (сторона/2)^2)).
- Подставляем известные значения: высота = (4 * √(4 - (4/2)^2)).
- Выполняем расчеты внутри скобок: высота = (4 * √(4 - 2^2)).
- Продолжаем расчеты: высота = (4 * √(4 - 4)).
- Выполняем вычитание: высота = (4 * √0).
- Так как корень из нуля равен нулю, вертикальная высота ромба равна 0.
- Делим диагональ пополам: 10 / 2 = 5.
- Подставляем полученное значение в формулу: высота = (сторона * √(4 - (сторона/2)^2)).
- Подставляем известные значения: высота = (6 * √(4 - (6/2)^2)).
- Выполняем расчеты внутри скобок: высота = (6 * √(4 - 9)).
- Выполняем вычитание: высота = (6 * √(-5)).
- Так как корень из отрицательного числа невозможен, этот ромб не имеет высоты.
- Делим диагональ пополам: 6 / 2 = 3.
- Подставляем полученное значение в формулу: высота = (сторона * √(4 - (сторона/2)^2)).
- Подставляем известные значения: высота = (3 * √(4 - (3/2)^2)).
- Выполняем расчеты внутри скобок: высота = (3 * √(4 - 2.25)).
- Выполняем вычитание: высота = (3 * √(1.75)).
- Вычисляем значение внутри корня: высота = (3 * √1.75).
- Округляем значение до двух знаков после запятой: высота ≈ 4.71.
Таким образом, высота ромба может быть равна 0, если диагональ делится пополам на сторону, или иметь положительное значение, если выражение под корнем больше нуля. Чтобы решить задачу, нужно использовать указанную формулу и подставлять в нее известные значения.
Некоторые полезные советы

Вот несколько полезных советов, которые помогут вам найти высоту ромба по заданной диагонали:
1. Проверьте, правильно ли вы измерили диагональ ромба. Для этого используйте линейку или мерный инструмент и убедитесь, что измерения точные.
2. Помните, что диагональ ромба делит его на два равносторонних треугольника. Используя эту информацию, вы можете использовать формулу для нахождения высоты треугольника, которая равна двум умножить на площадь треугольника, деленную на длину его основания.
3. Обратите внимание на единицы измерения, используемые в задаче. Если вам дана диагональ в сантиметрах, а высота ромба требуется в метрах, не забудьте перевести значения в одну систему измерений, чтобы избежать путаницы.
4. При выполнении вычислений не забывайте округлять результаты до необходимого количества знаков после запятой, если этого требует задача или ваше решение.
5. Запишите все промежуточные шаги и формулы, чтобы легче было проверить свое решение и найти возможные ошибки.
Следуя этим советам, вы сможете успешно найти высоту ромба по заданной диагонали и решить свою задачу с легкостью.