Высота трапеции – это одно из ключевых понятий геометрии, которое позволяет определить расстояние от одной основания трапеции до другого. Нахождение высоты трапеции является неотъемлемой частью ее геометрического анализа и находит широкое применение в различных задачах и расчетах.
Существует несколько способов нахождения высоты трапеции в зависимости от известных данных. Наиболее распространенным и простым способом является использование формулы, основанной на соотношении между высотой, основаниями и боковыми сторонами трапеции.
Для нахождения высоты трапеции, первым шагом необходимо определить известные данные. Это могут быть длины оснований, длины боковых сторон или углы трапеции. Затем, используя соответствующие формулы, можно найти значение высоты.
Чтобы упростить процесс нахождения высоты трапеции, можно воспользоваться подробным руководством, которое поможет разобраться в данной теме более подробно и решить любую задачу связанную с нахождением высоты трапеции.
Основные понятия для нахождения высоты трапеции
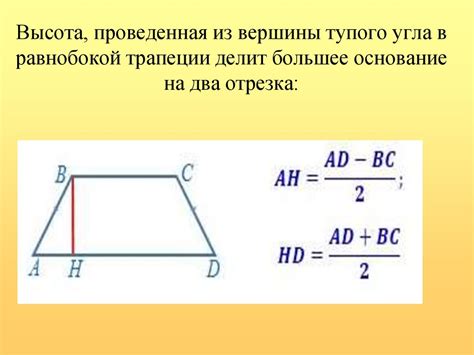
Высота трапеции - это отрезок, проведенный через основания и перпендикулярный к ним. Она является расстоянием между основаниями и определяет площадь трапеции.
Основные понятия, необходимые для нахождения высоты трапеции:
| Символ | Описание |
| h | Высота трапеции |
| a | Длина одного основания |
| b | Длина другого основания |
Для нахождения высоты трапеции можно воспользоваться различными способами. Один из способов - использовать теорему Пифагора для нахождения высоты, зная длины оснований и боковых сторон.
Важно помнить, что при использовании этой формулы основания должны быть перпендикулярны боковым сторонам, а боковые стороны - равны.
Что такое трапеция и какие у нее особенности?

- Основания трапеции - это пара ее параллельных сторон. Одно основание является верхней стороной, а другое - нижней стороной.
- Боковые стороны трапеции - это пара непараллельных сторон, соединяющих основания. Длины боковых сторон могут быть разными.
- Периметр трапеции - это сумма длин всех ее сторон.
- Высота трапеции - это отрезок, опущенный из одного основания к другому и перпендикулярный основаниям. Высота является основой для расчетов площади трапеции.
- Площадь трапеции - это произведение полусуммы ее оснований на высоту.
Трапеции широко применяются в геометрии и имеют множество приложений в реальной жизни. Знание основных особенностей трапеции важно для решения задач, связанных с расчетом ее площади, периметра и высоты.
Какие данные нам понадобятся для нахождения высоты?

Для нахождения высоты трапеции нам понадобятся следующие данные:
- Длина верхнего основания (a): это длина одной из параллельных сторон трапеции.
- Длина нижнего основания (b): это длина второй параллельной стороны трапеции.
- Длина боковой стороны (c): это длина одной из боковых сторон трапеции, которая соединяет верхнее и нижнее основания.
Эти данные необходимо знать перед тем, как приступить к расчету высоты трапеции. Обеспечивая точность и правильность вычислений, они позволяют нам определить высоту данной геометрической фигуры.
Метод нахождения высоты трапеции через основания
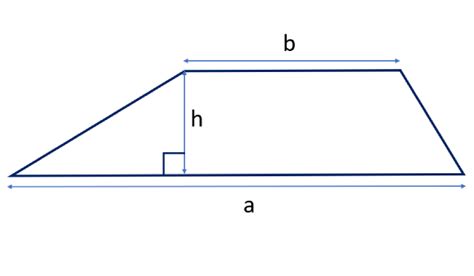
- Найдите разницу между длинами оснований трапеции: a и b.
- Обозначим высоту трапеции как h.
- Используя длины оснований и высоту, составьте уравнение:
- Решите уравнение, чтобы найти значение высоты.
(a - b) / 2 = h
Например, если длина большего основания a равна 10 см, а длина меньшего основания b равна 6 см, то по формуле:
(10 - 6) / 2 = h
Получаем:
4 / 2 = h
2 = h
Таким образом, высота трапеции равна 2 см.
Используя этот метод, вы можете легко найти высоту трапеции, если известны длины её оснований. Это полезно при решении задач и конструировании фигур.
Как использовать длины оснований для нахождения высоты?

Для нахождения высоты трапеции с известными длинами оснований и боковыми сторонами необходимо выполнять следующие шаги:
| Шаг | Описание |
|---|---|
| 1 | Измерьте длины оснований трапеции. Обозначим их как a и b. |
| 2 | Измерьте длину одной из боковых сторон трапеции. Обозначим ее как c. |
| 3 | Примените формулу для нахождения высоты трапеции: h = 2 * (a + b) / c. |
| 4 | Вычислите значение высоты с помощью рассчитанной формулы. |
| 5 | Проверьте результат, убедившись, что вы использовали правильные значения длин оснований и боковой стороны. |
Используя эти шаги, вы сможете легко вычислить высоту трапеции, используя известные длины оснований и боковой стороны. Этот метод особенно полезен при выполнении геометрических расчетов или при решении задач в школьной математике.
Метод нахождения высоты трапеции через боковые стороны

Метод нахождения высоты трапеции через боковые стороны основан на применении теоремы Пифагора. Для этого необходимо знать длину каждой из боковых сторон трапеции.
Шаги для нахождения высоты трапеции через боковые стороны:
- Определите длину каждой из боковых сторон трапеции.
- Используя теорему Пифагора, найдите квадрат суммы длин этих сторон.
- Выразите квадрат высоты трапеции через квадрат суммы боковых сторон.
- Извлеките корень из полученного значения, чтобы найти длину высоты трапеции.
Например, если боковые стороны трапеции равны 5 и 6, то шаги вычисления высоты будут следующими:
- Квадрат первой боковой стороны = 5^2 = 25.
- Квадрат второй боковой стороны = 6^2 = 36.
- Сумма квадратов боковых сторон = 25 + 36 = 61.
- Длина высоты трапеции = √61 = примерно 7.81.
Теперь вы знаете, как найти высоту трапеции через боковые стороны. Этот метод может быть полезен в различных задачах, связанных с трапециями, таких как вычисление площади или нахождение других параметров.
Как использовать длины боковых сторон для нахождения высоты?

Шаг 2: Рассмотрим трапецию ABCD, где AB и CD - основания трапеции, а AD и BC - боковые стороны. Предположим, что точка H - высота трапеции, опущенная из вершины D. Наша задача - найти длину высоты H.
Шаг 3: Разделим трапецию на два прямоугольных треугольника, AHD и BHC. Используя теорему Пифагора, можем записать следующие соотношения:
В треугольнике AHD:
AD2 = AH2 + HD2
В треугольнике BHC:
BC2 = BH2 + HC2
Шаг 4: Используя известные значения длин боковых сторон tрапеции (a и b), а также значения оснований (AB и CD), запишем уравнения:
AD = AB - CD
BC = CD - AB
Шаг 5: Подставим значения AD и BC в уравнения для треугольников AHD и BHC:
(AB - CD)2 = AH2 + HD2
(CD - AB)2 = BH2 + HC2
Шаг 6: Решим полученные уравнения для нахождения значений AH и BH. Для этого можно использовать алгебраические методы или калькулятор.
Шаг 7: Выберем значение из полученных решений, соответствующее высоте трапеции. Это значение будет длиной высоты H.
Примечание: Если полученные решения являются отрицательными или комплексными числами, значит, трапеция не существует при заданных значениях оснований и боковых сторон.