Треугольник - одна из самых простых и неотъемлемых геометрических фигур. Его структура определяется тремя сторонами и тремя углами. Одной из важнейших характеристик треугольника является его высота. Высота треугольника - это перпендикуляр, опущенный из вершины на основание или продолжение основания. Нахождение высоты треугольника является неотъемлемой частью задач геометрии и позволяет решать множество практических задач.
Одной из возможных ситуаций, в которых необходимо найти высоту треугольника, является случай, когда известна длина основания и прямой угол между основанием и высотой. Для решения этой задачи существует несколько способов, которые позволяют найти высоту треугольника при заданных условиях.
Один из таких способов - использование теоремы Пифагора. Для этого необходимо знать длину основания и расстояние от вершины треугольника до основания, а также использовать теорему Пифагора, которая устанавливает соотношение между длинами сторон прямоугольного треугольника: квадрат длины гипотенузы равен сумме квадратов длин катетов. Применение этой теоремы позволяет найти длину высоты и тем самым решить задачу.
Примеры и операции для нахождения высоты треугольника с заданным основанием и прямым углом
- Найдите длину основания треугольника.
- Зная длину основания и прямой угол, используйте теорему Пифагора для нахождения длины высоты треугольника.
Пример:
Пусть дан треугольник ABC, у которого основание AB равно 8 см, а угол ABC - прямой угол. Найдем высоту треугольника.
- Длина основания треугольника AB = 8 см.
- Используем теорему Пифагора: высота^2 + (AB/2)^2 = AB^2.
- Подставляем известные значения: высота^2 + (8/2)^2 = 8^2. Упрощаем уравнение: высота^2 + 16 = 64.
- Решаем получившееся уравнение: высота^2 = 64 - 16, высота^2 = 48.
- Находим высоту треугольника путем извлечения корня: высота = √48 = 6.93 см (округляем до двух десятичных знаков).
Таким образом, высота треугольника ABC равна 6.93 см.
Определение высоты треугольника по формуле и заданным значениям
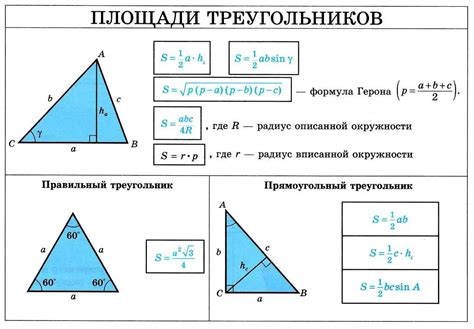
Формула для вычисления высоты треугольника выглядит следующим образом:
h = a * sin(α)
где:
h - высота треугольника;
a - длина основания треугольника;
α - значение прямого угла треугольника.
Для определения высоты треугольника, необходимо знать значения основания и прямого угла. Подставив эти значения в формулу, мы можем вычислить значение высоты.
Например, если у нас есть треугольник со стороной основания в 5 единиц и прямым углом, то значение высоты будет:
h = 5 * sin(90)
h = 5 * 1
h = 5
Таким образом, высота данного треугольника будет равна 5 единицам.
Используя данную формулу, можно определить высоту треугольника, если известны значения основания и прямого угла, что поможет в решении геометрических задач и вычислениях.
Операции по расчету высоты треугольника через основание и прямой угол
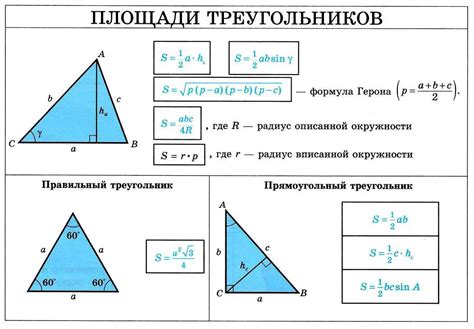
Для нахождения высоты треугольника, используется формула:
h = a*sin(A)
где:
- h - высота треугольника;
- a - длина основания треугольника;
- A - прямой угол между основанием и высотой треугольника.
Таким образом, для вычисления высоты треугольника через основание и прямой угол, необходимо знать длину основания и величину прямого угла.
Ниже приведен пример расчета высоты треугольника:
Допустим, у нас есть треугольник с основанием длиной 8 единиц и прямым углом. Чтобы найти высоту треугольника, мы можем использовать формулу и подставить известные значения:
h = 8 * sin(90)
Так как синус 90 градусов равен 1, мы можем упростить формулу:
h = 8 * 1
h = 8
Таким образом, высота треугольника равна 8 единицам.
Это лишь один из примеров расчета высоты треугольника через основание и прямой угол. Зная значения основания и прямого угла, можно легко вычислить высоту с помощью соответствующей формулы.
Применение геометрических операций для определения высоты треугольника
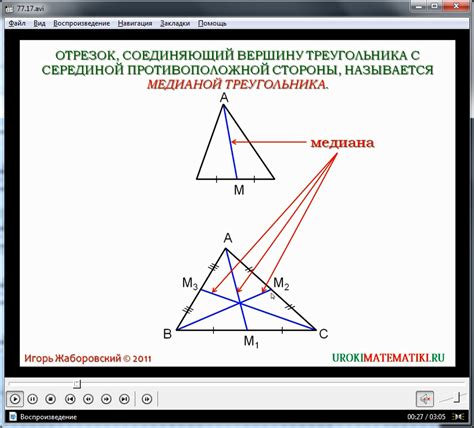
Если дано основание треугольника и известный прямой угол (прямой угол равен 90 градусам), то для определения высоты треугольника можно использовать следующую геометрическую операцию:
- Продолжить одну из сторон треугольника, проходящую через вершину на любое расстояние.
- Создать прямую линию, параллельную основанию треугольника и проходящую через продолженную сторону.
- Найти точку пересечения продолженной стороны с созданной прямой. Эта точка будет являться основанием перпендикуляра - точкой, из которой опущена высота треугольника.
- Провести прямую линию от вершины треугольника до найденной точки пересечения. Эта линия и будет являться высотой треугольника.
Применение данных геометрических операций позволяет с легкостью определить высоту треугольника, используя только основание и прямой угол.
Пример:
Дан треугольник ABC, где AB = 5 см, BC = 4 см, и угол ABC является прямым углом.
1. Продолжим сторону BC в направлении отрезка BC на любое расстояние.
2. Строим прямую линию, параллельную стороне АС и проходящую через продолженную сторону BC.
3. Найдем точку пересечения продолженной стороны BC с созданной прямой. Пусть эта точка будет D.
4. Проведем прямую линию, проходящую через точку A и точку D - это и будет высота треугольника.
Таким образом, мы определили высоту треугольника ABC, используя основание и прямой угол.
Решение задачи на нахождение высоты треугольника с использованием известных данных
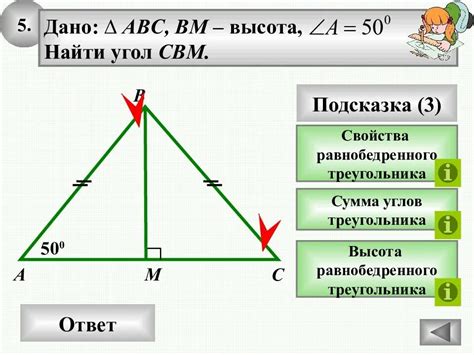
Для нахождения высоты треугольника с основанием и прямым углом мы можем использовать известные данные о треугольнике и применить соответствующую формулу.
Данная задача решается с использованием следующей формулы:
- высота треугольника = площадь треугольника / длина основания
Площадь треугольника может быть найдена с использованием различных методов, включая формулу Герона для нахождения площади треугольника по длинам его сторон, либо с использованием формулы для нахождения площади треугольника по длине его основания и высоте.
Допустим, у нас есть треугольник с заданным основанием и прямым углом. Мы знаем, что в прямоугольном треугольнике высота, проведенная к основанию, будет одновременно являться и высотой к противолежащему катету. Следовательно, для нахождения высоты треугольника мы можем использовать формулу:
- высота треугольника = площадь треугольника / длина основания = (1/2 * длина основания * длина основания) / длина основания = 1/2 * длина основания
Таким образом, высота треугольника равна половине длины его основания.
Например, если основание треугольника равно 6 единицам длины, то его высота будет равна 3 единицам длины.
Примеры решения задач с нахождением высоты треугольника по заданному основанию и прямому углу
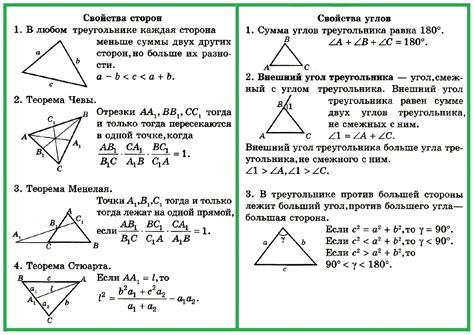
Для решения задачи, где необходимо найти высоту треугольника по заданному основанию и прямому углу, можно использовать следующий алгоритм.
1. Определите заданное основание треугольника.
2. Используя значение прямого угла, найдите значение синуса данного угла.
3. Вычислите высоту треугольника по формуле: высота = основание * синус угла.
4. Проверьте полученный результат и убедитесь, что он соответствует поставленной задаче.
Вот пример задачи:
Дан треугольник ABC, в котором угол B равен 90 градусам, а сторона AC равна 8 см. Необходимо найти высоту треугольника, проведенную к основанию BC.
Решение:
1. Основание треугольника - сторона BC.
2. Угол B равен 90 градусам, поэтому синус данного угла равен 1.
3. Высота треугольника равна основанию умноженному на синус угла: высота = 8 см * 1 = 8 см.
Ответ: высота треугольника, проведенная к основанию BC, равна 8 см.
Таким образом, примеры решения задач с нахождением высоты треугольника по заданному основанию и прямому углу сводятся к применению формулы высоты треугольника и вычислению значения синуса нужного угла.