Высота – важная физическая величина, которая используется в различных областях науки и инженерии. В физике, высота определяет расстояние от точки A до точки B в вертикальной плоскости. Знание высоты позволяет решать широкий спектр задач, от определения силы тяжести до рассчета времени падения объекта.
Существует несколько способов определения высоты в физике. Один из самых простых способов - измерение высоты с использованием линейки или мера длины. Однако, нередко в задачах требуется определить высоту, когда прямое измерение невозможно или непрактично. В таких случаях приходится применять формулы для рассчета высоты.
Формула для рассчета высоты в физике может быть различна в зависимости от задачи. Например, для расчета высоты падения свободно падающего объекта можно использовать формулу высоты падения в свободном поле тяжести: h = (1/2) * g * t^2, где h - высота, g - ускорение свободного падения, t - время падения. При таком подходе, для расчета высоты необходимо знать только ускорение свободного падения и время падения.
Методы расчета высоты в физике

В физике существуют различные методы расчета высоты для разных объектов и ситуаций. Рассмотрим некоторые из них:
1. Высота свободного падения:
Для расчета высоты свободного падения можно использовать формулу высоты падения тела в зависимости от времени:
h = (1/2) * g * t^2,
где h - высота падения, g - ускорение свободного падения, t - время падения.
2. Высота подъема:
Для расчета высоты подъема тела можно использовать принцип сохранения энергии, учитывая потенциальную энергию тела до и после подъема:
mgh = mgh' + ΔE,
где m - масса тела, g - ускорение свободного падения, h - начальная высота, h' - конечная высота, ΔE - изменение кинетической энергии тела.
3. Высота с помощью звука:
Для определения высоты с помощью звука можно использовать эхолокацию или измерять задержку между излучением звука и его отражением.
Это лишь некоторые из методов расчета высоты в физике. Каждый метод имеет свои особенности и может быть применен в разных ситуациях.
Использование формулы высоты

| Формула | Описание |
|---|---|
| h = v * t | Формула вычисления высоты, где h - высота, v - скорость движения, t - время движения |
| h = (1/2) * g * t^2 | Формула вычисления высоты при вертикальном броске предмета, где h - высота, g - ускорение свободного падения, t - время падения |
| h = v^2 / (2 * g) | Формула вычисления максимальной высоты подъема предмета при вертикальном броске, где h - максимальная высота, v - начальная скорость, g - ускорение свободного падения |
Расчет высоты с использованием этих формул обычно основывается на известных данных о движении и атмосферных условиях. Например, для определения высоты здания с помощью первой формулы, необходимо измерить скорость движения объекта, например, электронного сигарета, и время, за которое она перемещается вверх. Подставив эти значения в формулу, можно рассчитать высоту здания.
Важно отметить, что при использовании формул высоты необходимо учитывать различные факторы, такие как влияние силы трения, изменение ускорения свободного падения с высотой и другие. Также следует помнить, что формулы являются моделями реальности и могут давать приближенные значения высоты, а не точные.
Применение тригонометрии для определения высоты

Одним из способов применения тригонометрии для определения высоты является использование теоремы синусов. Эта теорема позволяет связать отношение длин сторон треугольника синусом его углов. Используя теорему синусов, можно построить прямоугольный треугольник, где один из углов известен, а другой можно измерить или задать некоторым образом.
Для определения высоты с помощью теоремы синусов необходимо измерить или задать следующие параметры:
- Длину основания треугольника - это горизонтальное расстояние от точки, из которой измеряется высота, до основания объекта.
- Значение угла между прямой, проведенной от точки измерения высоты к основанию объекта, и горизонтом.
- Длину противоположной стороны треугольника - это высота объекта, которую мы пытаемся определить.
После измерения или задания этих параметров, можно рассчитать высоту объекта с помощью следующей формулы:
высота = (длина основания) * sin(угол)
Важно помнить, что значения должны быть выражены в соответствующих единицах измерения и используемый угол должен быть в радианах.
Таким образом, применение тригонометрии и теоремы синусов позволяет определить высоту объекта, используя измерения и заданные углы. Это может быть полезно в различных задачах в физике, где точное определение высоты не всегда возможно.
Измерение высоты с помощью барометра

Один из способов определить высоту над уровнем моря, используя принцип работы барометра. Барометр позволяет измерить атмосферное давление, которое меняется с изменением высоты.
Для проведения измерений необходимо знать приближенное значение атмосферного давления, которое можно получить из метеорологических данных или с использованием онлайн-сервисов. Затем, с помощью барометра, можно измерить текущее атмосферное давление в заданной точке.
Принцип расчета высоты основан на изменении атмосферного давления с высотой. Обычно, давление уменьшается с увеличением высоты, поэтому можно использовать эту зависимость для определения высоты над уровнем моря.
- Запишите текущее атмосферное давление в миллиметрах ртутного столба (мм рт.ст.)
- Используя данные из метеорологических источников, определите атмосферное давление на уровне моря в мм рт.ст.
- Вычтите значение атмосферного давления на уровне моря из текущего значения атмосферного давления. Полученная разница будет показывать изменение давления с высотой.
- Используйте уравнение между атмосферным давлением и высотой для определения высоты. Величина гравитационного ускорения, температура окружающей среды и атмосферная составляющая влияют на данное уравнение. Для более точных результатов, рекомендуется использовать специализированные программы или сайты, которые учитывают эти факторы.
Измерение высоты с помощью барометра может быть полезным для определения высоты горных пиков, наблюдательных площадок или любых других точек относительно уровня моря. Однако, стоит помнить, что данная методика имеет некоторую погрешность и может быть ограничена влиянием погодных условий и других факторов.
Метод определения высоты с помощью GPS-навигации
GPS-навигация может использоваться для определения высоты над уровнем моря с помощью специальных алгоритмов и формул.
В процессе определения высоты с помощью GPS-навигации необходимо иметь доступ к достаточному количеству спутников, чтобы получить точные данные. GPS-приемник, встроенный в мобильные устройства или специальные навигационные приборы, может обрабатывать сигналы от нескольких спутников одновременно, что дает возможность определить геопозицию с высокой точностью.
Для получения высоты с помощью GPS-навигации используется алгоритм, известный как "дифференциальное позиционирование". Этот алгоритм позволяет измерить разницу сигналов, полученных от спутников, что позволяет определить высоту точки над уровнем моря.
Однако, важно иметь в виду, что определение высоты с помощью GPS-навигации не всегда обеспечивает абсолютную точность. Возможны ошибки из-за различных факторов, например, погодных условий или наличия препятствий, которые могут привести к искажению сигнала.
Поэтому при использовании GPS-навигации для определения высоты следует учитывать возможные погрешности и использовать дополнительные методы и данных для повышения точности измерений. Тем не менее, эта техника является широко распространенной и обеспечивает приемлемую точность для большинства приложений, требующих определения высоты.
В зависимости от конкретных требований и задачи, существует несколько формул и подходов для определения высоты с помощью GPS-навигации, но основным принципом остается использование спутниковых сигналов и алгоритмов коррекции для получения наиболее точных результатов.
Важно отметить, что использование GPS-навигации для определения высоты не является единственным методом, и существуют другие способы, такие как измерение атмосферного давления или использование специальных инструментов и сенсоров.
Однако GPS-навигация остается одним из наиболее доступных и удобных способов определения высоты с точки зрения практического использования в повседневной жизни и в различных областях, включая геодезию, геологию, туризм и другие. Вместе с тем, использование дополнительных данных и методов позволяет повысить точность и надежность измерений.
Расчет высоты с использованием уравнения движения тела в вертикальном направлении

Для расчета высоты объекта, движущегося в вертикальном направлении, можно использовать уравнение движения тела в данном случае.
Уравнение движения тела в вертикальном направлении имеет вид:
h = v₀t + ½gt²
где:
h - высота объекта на момент времени t;
v₀ - начальная вертикальная скорость объекта;
t - время, прошедшее с начала движения;
g - ускорение свободного падения (примерно 9,8 м/с²).
Для расчета высоты объекта необходимо знать начальную вертикальную скорость и время, прошедшее с начала движения. Подставив эти показатели в уравнение, можно получить значение высоты.
Например, если объект был брошен вертикально вверх с начальной скоростью 10 м/с и прошло 2 секунды, то высота на этот момент будет равна:
h = (10 м/с) * (2 с) + ½ * (9,8 м/с²) * (2 с)² = 20 м + 19,6 м = 39,6 м.
Таким образом, после 2 секунд движения объект находится на высоте 39,6 метра.
Использование данного уравнения позволяет легко и точно рассчитать высоту объекта, движущегося в вертикальном направлении. Это полезный инструмент не только в физике, но и в различных инженерных и научных областях.
Альтернативные способы определения высоты

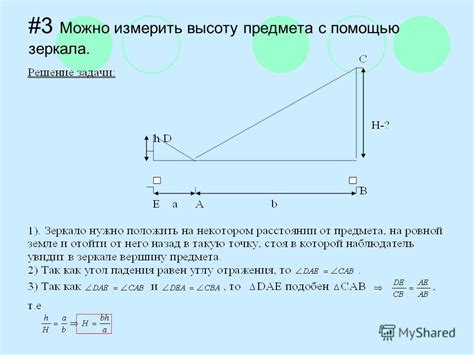
Один из таких методов – метод треугольника. Для использования этого метода необходимо иметь две разные точки наблюдения и измерить угол между прямой, проходящей через эти точки, и горизонтом. Затем, при помощи геометрических выкладок, можно определить высоту объекта в отношении к наблюдателю.
Другой способ – использование барометра. Барометр – это прибор, который позволяет измерять атмосферное давление. Используя таблицы или формулы, можно связать изменение атмосферного давления с изменением высоты над уровнем моря. Этот метод можно применять для определения высоты горных вершин или зданий.
Также современные технологии предлагают нам другие альтернативные способы измерения высоты, такие как использование спутниковой навигации (GPS) или беспилотных летательных аппаратов (дронов). С их помощью можно точно определить высоту объекта без необходимости проведения сложных вычислений.
В каждом из этих способов есть свои преимущества и ограничения, и выбор метода зависит от конкретной ситуации и доступных инструментов. Важно помнить, что правильное определение высоты является ключевым фактором для точных измерений и расчетов в физике.