Как найти высоту в равнобедренном треугольнике для учащихся 7 класса

Высота равнобедренного треугольника является одной из важных составляющих элементов этой геометрической фигуры. В равнобедренном треугольнике две стороны равны между собой, а третья - высота - перпендикулярна к основанию. Найти высоту в равнобедренном треугольнике несложно, если знать определенные формулы и принципы геометрии. В этой статье мы рассмотрим, как можно вычислить высоту в равнобедренном треугольнике для учащихся 7 класса.

Одним из способов определить высоту в равнобедренном треугольнике является использование формулы Герона. Формула Герона позволяет вычислить площадь треугольника, а затем посчитать высоту, используя соответствующие формулы. Этот способ основан на использовании полупериметра треугольника и длин его сторон.

Другой способ нахождения высоты в равнобедренном треугольнике - это использование теоремы Пифагора. Теорема Пифагора устанавливает соотношение между длиной гипотенузы и катетов в прямоугольном треугольнике. Применение этой теоремы в равнобедренном треугольнике позволяет найти длину высоты, используя длины сторон треугольника.

Определение треугольника и его высоты

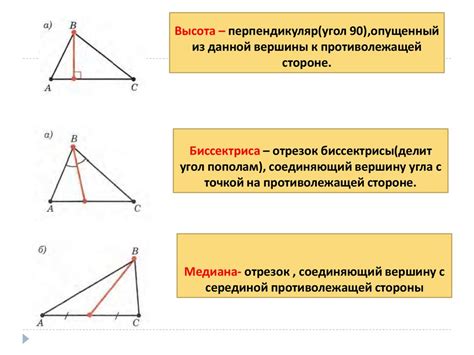
Высота треугольника - это отрезок, соединяющий вершину треугольника с противолежащей стороной и перпендикулярный к этой стороне. Высота может выпускаться из любой из трех вершин треугольника.

В равнобедренном треугольнике, две стороны равны друг другу и два угла при основании равны. Основание треугольника - это сторона, к которой выпущена высота.

Для определения высоты в равнобедренном треугольнике, можно воспользоваться различными методами:

• Использование теоремы Пифагора, если известна длина основания и боковой стороны;
• Использование формулы площади треугольника, если известна длина основания и высоты;
• Использование выпуклого угла треугольника и косинуса, если известен угол и длина основания.

Зная основание и одну из сторон равнобедренного треугольника, можно легко определить его высоту с помощью указанных методов.

Что такое равнобедренный треугольник?

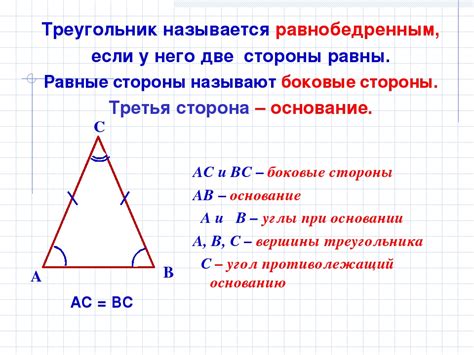
В равнобедренном треугольнике вершина, из которой выходят равные боковые стороны, называется вершиной равнобедренного треугольника. Также в равнобедренном треугольнике два угла при основании равны между собой и называются углами при основании.

Для равнобедренного треугольника с основанием a и равными боковыми сторонами b, высота h может быть найдена используя теорему Пифагора. Высота будет равна:

h = sqrt(b^2 - (a/2)^2)

Особенности равнобедренного треугольника

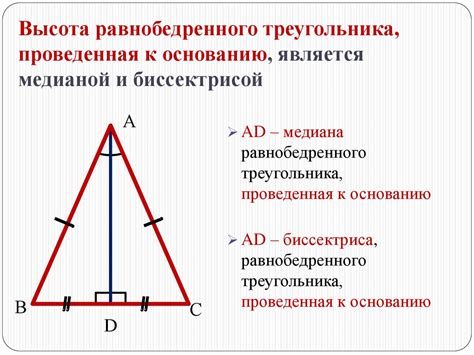
Первая особенность равнобедренного треугольника заключается в том, что высота, опущенная из вершины треугольника на основание, проходит через середину этого основания. Это означает, что пунктир, проведенный из вершины, будет пересекать основание в его середине.

Другая особенность равнобедренного треугольника связана с его углами. Так как две стороны равны, то и два угла у основания равны между собой. Кроме того, вершина угла, образованного основанием и высотой, делит противоположный угол пополам.

Эти особенности равнобедренного треугольника позволяют применять различные методы для нахождения его высоты и других значений. Например, если известна длина основания и требуется найти высоту, можно воспользоваться теоремой Пифагора или формулой площади треугольника. Если известны длины сторон, можно использовать теорему косинусов или теорему синусов для нахождения углов и других значений.

Исследование и применение особенностей равнобедренного треугольника позволяют упростить решение задач, связанных с его геометрическими характеристиками. Знание этих особенностей поможет в изучении геометрии и решении задач на практике.

Как найти высоту равнобедренного треугольника

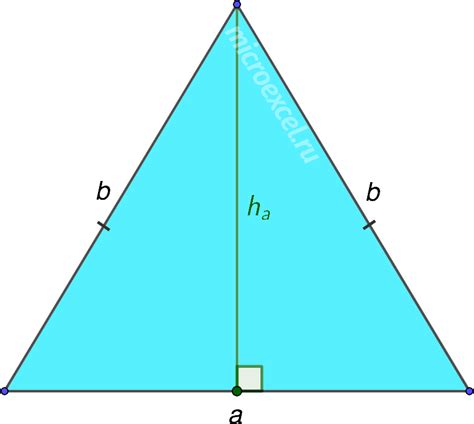
Если известны длины основания и стороны треугольника, можно использовать теорему Пифагора. Пусть основание равнобедренного треугольника равно a, а сторона равна b. Тогда, чтобы найти высоту h, нужно воспользоваться формулой:

h = √(b^2 - (a/2)^2)

Если известны длины стороны и значение угла между основанием и этой стороной, можно использовать тригонометрические функции. Пусть сторона равна a, а угол между основанием и этой стороной равен α. Тогда, чтобы найти высоту h, нужно воспользоваться формулой:

h = a * sin(α)

Высота равнобедренного треугольника играет важную роль при вычислении его площади и определении некоторых других свойств треугольника. Поэтому знание методов нахождения высоты позволяет более полно изучить эту геометрическую фигуру.

Метод 1: С использованием формулы

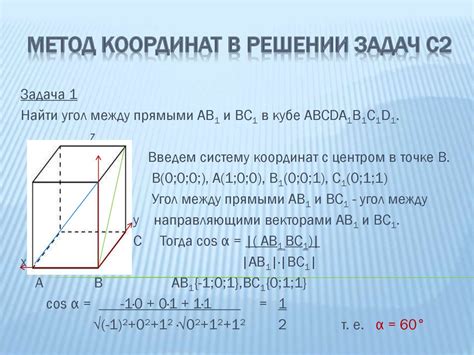
Для нахождения высоты равнобедренного треугольника можно использовать формулу, основанную на его свойствах:

• Равнобедренный треугольник имеет две равные стороны
• Высота, опущенная из вершины треугольника на основание, делит его на два равных прямоугольных треугольника

Для вычисления высоты треугольника можно использовать формулу:

h = √(a^2 - (b/2)^2)

Где:

• h - высота треугольника
• a - длина основания треугольника
• b - длина одной из равных сторон треугольника

Таким образом, чтобы найти высоту равнобедренного треугольника, необходимо знать длину основания и одной из равных сторон. Подставьте значения в формулу и решите ее, чтобы получить значение высоты треугольника.

Метод 2: С использованием геометрической конструкции

Для нахождения высоты в равнобедренном треугольнике можно использовать геометрическую конструкцию. В этом методе мы будем использовать свойство равнобедренных треугольников, которое гласит, что высота, опущенная из вершины равнобедренного треугольника, делит основание на две равные части.

Чтобы найти высоту, выполните следующие шаги:

1. Нарисуйте равнобедренный треугольник, в котором дано значение основания и значение одного из углов.
2. Из вершины треугольника опустите перпендикуляр на основание.
3. Перпендикуляр разделит основание на две равные части.
4. Из вершины треугольника опустите второй перпендикуляр на основание.
5. Определите точку пересечения обоих перпендикуляров.
6. Отметьте эту точку как основание высоты.
7. Из этой точки проведите линию до вершины треугольника.
8. Эта линия и будет высотой равнобедренного треугольника.

Используя этот метод, вы сможете точно найти значение высоты в заданном равнобедренном треугольнике и использовать его для решения различных задач.

Примеры решения задачи на высоту равнобедренного треугольника

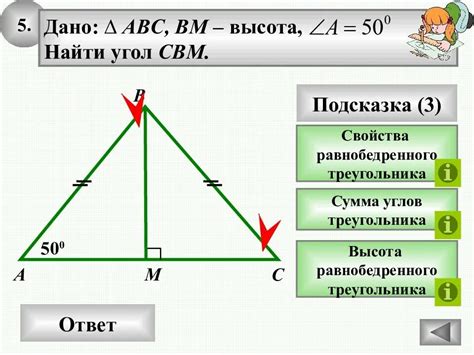
Для нахождения высоты равнобедренного треугольника, можно использовать следующие формулы и методы:

1. Вписанный равнобедренный треугольник:

2. РАвносторонний треугольник:

3. Стороны и углы:

Если известны длины сторон треугольника и один из его углов, можно использовать теорему синусов:

H = b * sin(α), где:

• b - длина основания треугольника
• α - угол, противолежащий основанию треугольника