Определение высоты в треугольнике

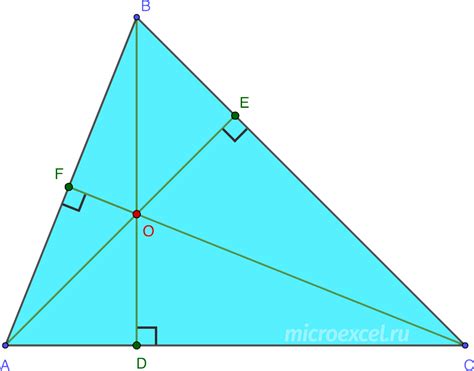
Высота треугольника - это сегмент, перпендикулярный основанию (прямой, соединяющей два крайних угла треугольника). Высота делит треугольник на два треугольника равной площади.

Как найти высоту в треугольнике через основание

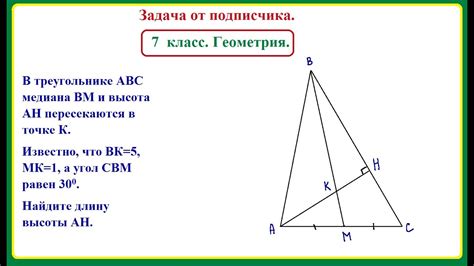
Для нахождения высоты треугольника, если известна его основание (любая сторона) и высота опущена на это основание, можно использовать следующую формулу:

Высота треугольника = (2 * Площадь треугольника) / Основание треугольника

Формула может быть переписана следующим образом:

h = (2 * S) / a

Где:

• h - высота треугольника
• S - площадь треугольника
• a - основание треугольника

Обратите внимание, что площадь треугольника может быть вычислена по формуле:

S = (a * h) / 2

Примеры нахождения высоты в треугольнике

Рассмотрим несколько примеров, чтобы лучше понять процесс вычисления высоты в треугольнике через основание:

1. Пример 1:

Дано: треугольник со стороной основания a = 10 и площадью S = 30.

Вычисление: h = (2 * 30) / 10.

Ответ: h = 6.

2. Пример 2:

Дано: треугольник со стороной основания a = 8 и площадью S = 16.

Вычисление: h = (2 * 16) / 8.

Ответ: h = 4.

Таким образом, мы можем видеть, что вычисление высоты в треугольнике через основание является простой задачей, если известны значения площади и основания треугольника.

Методы нахождения высоты треугольника через основание

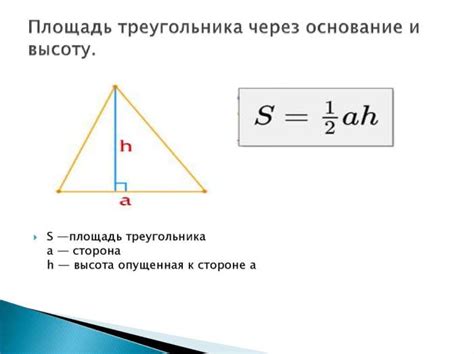
Существуют несколько методов нахождения высоты треугольника через основание:

1. Использование формулы высоты

Для поиска высоты треугольника можно использовать следующую формулу:

h = 2*площадь треугольника / основание треугольника

Где h - высота треугольника, площадь треугольника можно найти, зная его основание и высоту, а основание - одна из сторон треугольника.

2. Применение теоремы Пифагора

Если известны длины всех сторон треугольника, можно найти высоту с помощью теоремы Пифагора. Для этого необходимо определить, которая из сторон является основанием, а затем используйте теорему Пифагора, чтобы найти длину прилежащего к основанию отрезка (катета).

3. Использование подобия треугольников

Если треугольник подобен другому треугольнику, можно использовать соответствующие стороны, чтобы найти высоту треугольника через его основание. Для этого необходимо найти соответствующие стороны подобных треугольников и использовать их отношение для нахождения высоты.

Таким образом, нахождение высоты треугольника через его основание варьируется в зависимости от имеющихся данных. Используйте соответствующую формулу или метод, чтобы решить задачу и найти высоту треугольника в конкретном случае.