Диаметр окружности - это отрезок, соединяющий две наиболее удаленные точки на окружности. Если вам известен диаметр, вы легко можете найти другие характеристики окружности, например, длину хорды. Хорда - это отрезок, соединяющий две точки на окружности. Если диаметр проходит через середину хорды, то хорда является диаметром.
Чтобы найти длину хорды, используйте формулу: l = 2 * r * sin(a/2), где l - длина хорды, r - радиус окружности, a - угол между хордой и радиусом, проведенным к точке пересечения хорды с окружностью.
Если у вас есть диаметр, то это означает, что радиус равен половине диаметра. Используйте эту информацию в формуле для нахождения длины хорды. Не забудьте также измерить угол между хордой и радиусом, чтобы получить точный результат.
Определение хорды через диаметр окружности
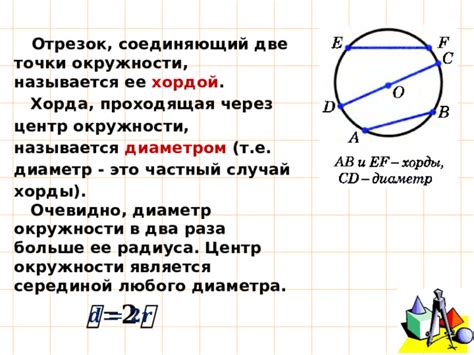
Длина хорды равна произведению диаметра на синус половины центрального угла, охватываемого этой хордой.
Формула записывается следующим образом:
Длина хорды = 2 * R * sin(α/2), где R - радиус окружности, α - мера центрального угла в радианах.
Таким образом, для определения хорды необходимо знать лишь диаметр окружности и меру центрального угла, охватываемого этой хордой.
Теперь вы сможете легко определить длину хорды через диаметр окружности. Это очень полезное знание, которое может пригодиться в решении геометрических задач и при работе с окружностями.
Что такое хорда и диаметр
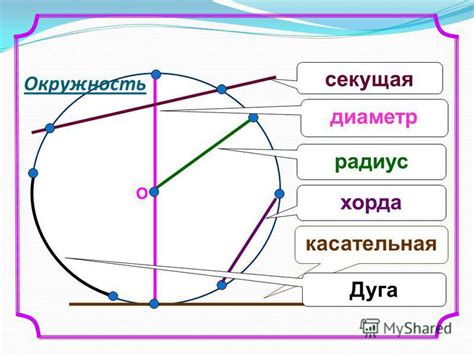
Хорда - это отрезок, соединяющий две точки на окружности. Хорда проходит внутри окружности и ее концы лежат на окружности.
Пример: если мы возьмем две точки A и B на окружности, отрезок AB будет являться хордой окружности.
Диаметр является частным случаем хорды. Диаметр - это хорда, проходящая через центр окружности.
Пример: пусть O - центр окружности, если мы возьмем две точки A и B на окружности, такие что AB проходит через O, то AB является диаметром окружности.
Таким образом, диаметр является самой длинной хордой в окружности и имеет особое значение, так как проходит через центр и делит окружность на две равные части.
Методы нахождения хорды через диаметр

Методы нахождения хорды через диаметр включают следующие приемы:
Использование теоремы о перпендикулярности диаметра и хорды:
- Постройте окружность с заданным диаметром.
- Выберите точку на окружности, не являющуюся концами диаметра.
- Проведите хорду, соединяющую выбранную точку с концами диаметра.
- Используя теорему о перпендикулярности диаметра и хорды, докажите, что проведённая хорда является хордой окружности.
Использование формулы для нахождения длины хорды через диаметр:
- Задайте диаметр окружности.
- Используя формулу для нахождения длины хорды через диаметр (L = sqrt(2r^2 - d^2), где L - длина хорды, r - радиус окружности, d - диаметр), вычислите длину хорды.
Использование свойств хорд, параллельных диаметру:
- Постройте окружность с заданным диаметром.
- Выберите точку на окружности, не являющуюся концами диаметра.
- Проведите хорду, параллельную заданному диаметру.
- Найдите хорду, соединяющую выбранную точку с концами диаметра и параллельную заданной хорде.
Используя один из указанных методов, вы сможете легко найти хорду в окружности через её диаметр и расширить свои знания в геометрии.
Геометрический метод

Для нахождения хорды в окружности через диаметр существует геометрический метод. Этот метод основан на свойствах окружности и позволяет без использования сложных формул и вычислений определить нужную хорду.
Шаги по использованию геометрического метода:
- Получите информацию о диаметре окружности.
- Найдите середину диаметра путем проведения перпендикуляра к нему.
- Проведите прямую через середину диаметра и точку на окружности, которая является концом хорды.
- Продолжите прямую через середину диаметра до тех пор, пока она не пересечет окружность.
- Проведите прямую от центра окружности до точки пересечения продолженной прямой с окружностью.
- Получившаяся отрезок будет являться хордой.
Геометрический метод является простым и понятным способом нахождения хорды в окружности через диаметр. Он позволяет избежать сложных вычислений и применения формул, что делает его доступным для решения задач разной сложности.
Аналитический метод

- Выбрать систему координат на плоскости, где центр окружности с координатами (0, 0) и диаметр лежит на оси OX.
- Записать уравнение окружности в виде x^2 + y^2 = r^2, где r – радиус окружности.
- Найти точки пересечения окружности с осью OX, это будут точки A(-r, 0) и B(r, 0).
- Выбрать произвольную точку C(x, y) на окружности.
- Найти уравнение прямой AC, используя формулу (y - y1) / (y2 - y1) = (x - x1) / (x2 - x1), где x1, y1 – координаты точки A, x2, y2 – координаты точки C.
- Найти координаты точки D(x, -y), которая является точкой пересечения хорды AC с осью OX.
Теперь вы знаете, как найти хорду в окружности через диаметр с помощью аналитического метода. Этот метод позволяет получить точные значения координат хорды и провести ее на плоскости без каких-либо проблем.