Функции являются одной из основных концепций в математике. Они описывают зависимость между входными и выходными значениями, позволяющую анализировать и предсказывать различные явления в реальном мире. Нахождение значения функции от заданного числа – важная задача, которая часто встречается в различных областях знаний.
Значение функции – это результат ее вычисления для определенного входного значения. Существует множество способов найти значение функции от числа, в зависимости от типа функции и доступной информации.
Одной из самых простых и распространенных методик является подстановка числа в функцию. Если у вас есть аналитическое выражение функции, вы можете просто заменить входное число на его значение и выполнить необходимые математические операции, чтобы получить результат. Например, если у вас есть функция f(x) = 2x + 3, и вам нужно найти значение функции для x = 5, вы можете заменить x на 5 и выполнить вычисления: f(5) = 2 * 5 + 3 = 13.
Еще одним способом нахождения значения функции от числа является построение графика функции и определение значения в заданной точке. График функции представляет собой визуальное изображение ее зависимости от входных и выходных значений. Построив график, вы можете найти значение функции для заданного числа, определив точку на графике с соответствующей координатой. Например, если у вас есть график функции f(x), и вам нужно найти значение функции для x = 3, вы можете определить точку на графике с координатами (3, y), где y будет являться значением функции.
Определение функции и ее значение

Значение функции - это результат применения функции к определенному аргументу. Для каждого аргумента x функция f может иметь только одно значение. Значение функции обычно обозначается символом y и записывается в виде y = f(x).
Чтобы найти значение функции от заданного числа, необходимо подставить это число вместо аргумента x в записи функции и вычислить полученное выражение. Например, если функция f(x) = 2x + 3, то значение функции от числа 5 можно найти, подставив 5 вместо x: f(5) = 2 * 5 + 3 = 13. Таким образом, значение функции от числа 5 равно 13.
Если функция задана в виде таблицы значений, то значение функции от заданного числа можно найти, находим строку в таблице соответствующую заданному числу в столбце аргументов, и затем находим значение функции в соответствующей строке в столбце значений. Например, если задана функция f(x), и ее таблица значений выглядит следующим образом:
| x | f(x) |
|---|---|
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
Чтобы найти значение функции от числа 2, нужно найти строку с аргументом 2 и в соответствующей строке в столбце значений найти значение функции. В данном случае, значение функции от числа 2 равно 7.
Что такое функция и как ее использовать

Функции используются для упрощения программирования и повторного использования кода. Они могут принимать значения в качестве параметров и возвращать результаты. Функции могут быть определены в программе или библиотеке и могут использоваться многократно в разных частях программы.
Для использования функции нужно выполнить следующие шаги:
- Определить функцию с помощью ключевого слова "function" и указать ее имя и параметры, если они есть.
- Написать код функции внутри фигурных скобок. Код может включать любые операции и инструкции.
- При необходимости передать значения параметров в функцию.
- Вызвать функцию, указав ее имя и передав значения параметров.
- Получить результат работы функции, если она его возвращает.
Пример использования функции:
| Пример | Описание |
|---|---|
function multiply(x, y) { | Определение функции "multiply", которая принимает два параметра и возвращает их произведение. |
let result = multiply(2, 3); | Вызов функции "multiply" с аргументами 2 и 3. |
Таким образом, функции позволяют упростить программирование, улучшить читаемость кода и повторно использовать его в различных частях программы.
Как определить значение функции от числа
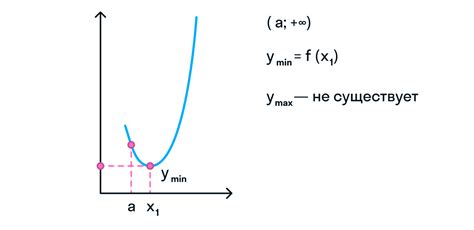
- Шаг 1: Задайте функцию. В начале вы должны иметь функцию, для которой необходимо определить значение. Функция может быть задана в виде алгебраического выражения или графика.
- Шаг 2: Задайте число. Выберите число, для которого вы хотите определить значение функции. Это число может быть любым действительным числом, в зависимости от области определения функции.
- Шаг 3: Подставьте число в функцию. Замените переменную в алгебраическом выражении функции на выбранное число. Если функция задана графиком, найдите соответствующую точку на графике для заданного числа.
- Шаг 4: Вычислите результат. Вычислите значение функции, подставив число вместо переменной в алгебраическом выражении функции или определив значение функции на графике.
Пример:
Задана функция f(x) = 3x + 2. Необходимо найти значение функции для числа x = 5.
- Шаг 1: Функция задана: f(x) = 3x + 2
- Шаг 2: Число задано: x = 5
- Шаг 3: Подставляем число в функцию: f(5) = 3 * 5 + 2 = 15 + 2 = 17
- Шаг 4: Результат: Значение функции для числа 5 равно 17. То есть, f(5) = 17.
В результате выполнения всех шагов мы получили значение функции для заданного числа. Этот процесс может быть применен для любой заданной функции и числа.
Как найти значение функции от числа вручную
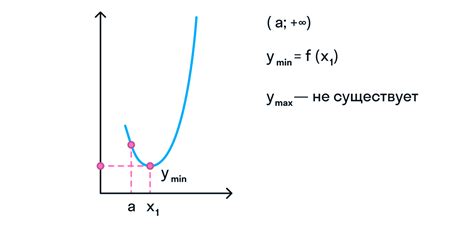
Для того чтобы найти значение функции от заданного числа, следует выполнить несколько простых шагов:
1. Определите функцию, для которой нужно найти значение. Функция может быть задана аналитически (с помощью формулы) или в виде набора значений в таблице.
2. Если функция задана аналитически, подставьте заданное число вместо переменной в формулу функции. Произведите необходимые математические операции, чтобы вычислить значение функции. Например, если функция задана как f(x) = x^2 + 2x, а необходимо найти значение для x = 3, то подставим 3 вместо x в формулу и выполним вычисления: f(3) = 3^2 + 2 * 3 = 9 + 6 = 15.
3. Если функция задана в виде набора значений в таблице, найдите значение функции, соответствующее заданному числу, в таблице. Как правило, значения в таблице задаются для определенного диапазона чисел, поэтому если заданное число не совпадает точно с каким-либо числом в таблице, следует выполнить интерполяцию для приближенного значения.
4. Проверьте полученный результат на правильность и округлите его до необходимой точности, если требуется.
Применение этих шагов поможет вам найти значение функции от заданного числа без необходимости использовать специальные программы или калькуляторы.
Шаги для нахождения значения функции
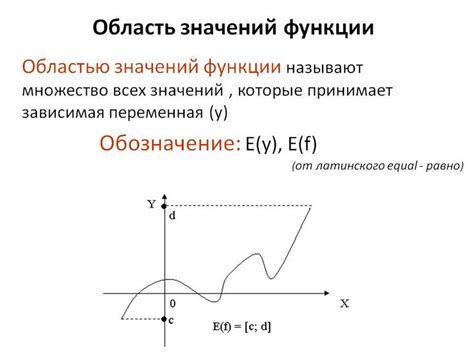
Для нахождения значения функции от числа необходимо следовать определенным шагам:
1. Задать функцию.
Определите функцию, для которой вы хотите найти значение от определенного числа. Функция может быть любой, например, линейной, квадратичной или тригонометрической.
2. Задать значение числа.
Определите число, для которого нужно найти значение функции. Обозначьте его, например, как x.
3. Подставить значение числа в функцию.
Подставьте значение числа (x) вместо переменной в функции. Если функция содержит более одной переменной, замените все переменные соответствующими значениями.
4. Вычислить значение функции.
После подстановки значения числа в функцию, вычислите значение функции, выполнив необходимые арифметические операции.
5. Получить конечный результат.
Полученное значение является значением функции от заданного числа.
Например, если задана функция f(x) = 2x + 3, а нужно найти значение функции для x = 5, то следуя описанным шагам:
1. Задаем функцию: f(x) = 2x + 3
2. Задаем значение числа: x = 5
3. Подставляем значение числа в функцию: f(5) = 2 * 5 + 3
4. Вычисляем значение функции: f(5) = 10 + 3 = 13
5. Получаем конечный результат: значение функции f(5) равно 13.
Примеры решения уравнений с нахождением значения функции

Для нахождения значения функции от заданного числа нужно подставить это число вместо переменной в уравнение и выполнить необходимые вычисления. Рассмотрим несколько примеров:
Пример 1:
Дана функция f(x) = 2x + 3. Найдем значение функции при x = 4.
Подставляем x = 4 вместо x в уравнение:
f(4) = 2 * 4 + 3 = 8 + 3 = 11.
Таким образом, значение функции при x = 4 равно 11.
Пример 2:
Дана функция f(x) = x^2 - 5x + 6. Найдем значение функции при x = 2.
Подставляем x = 2 вместо x в уравнение:
f(2) = 2^2 - 5 * 2 + 6 = 4 - 10 + 6 = 0.
Таким образом, значение функции при x = 2 равно 0.
Пример 3:
Дана функция f(x) = √(x - 4). Найдем значение функции при x = 9.
Подставляем x = 9 вместо x в уравнение:
f(9) = √(9 - 4) = √5.
Таким образом, значение функции при x = 9 равно √5.
Таким образом, для нахождения значения функции от числа нужно заменить переменную на это число в уравнении и выполнить вычисления.
Использование математических формул для нахождения значения функции
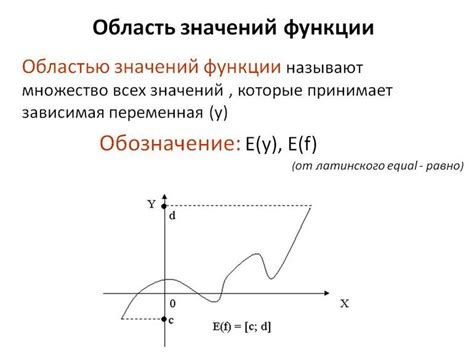
Взглянем на простой пример. Пусть у нас есть функция f(x) = 2x + 3. Чтобы найти значение функции при определенном числе x, нужно подставить это число в формулу и выполнить необходимые математические операции. Например, если мы хотим найти f(5), то подставим x = 5 в формулу: f(5) = 2 * 5 + 3 = 13.
Также, для некоторых функций существуют таблицы значений, которые упрощают процесс нахождения значений функции. Например, для функции y = x^2 + 1 можно составить таблицу со значениями x и соответствующими им значениями y:
| x | y |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 5 |
| 3 | 10 |
| 4 | 17 |
Используя данную таблицу, мы можем заполнить значения функции для определенных x и легко найти значение функции для любого числа.
Примеры простых функций и их значения от числа

В математике функция определяется как соответствие между элементами двух множеств, где каждому элементу первого множества соответствует ровно один элемент второго множества. Функции могут быть очень разнообразными и выполнять различные операции с числами.
Простыми функциями могут быть, например:
- Функция умножения на два: данное число умножается на два.
- Функция возведения в квадрат: данное число умножается само на себя.
- Функция вычитания трех: из данного числа вычитается три.
Рассмотрим примеры простых функций и их значения от числа 5:
1. Функция умножения на два: 10. То есть, когда мы подставляем число 5 в эту функцию, мы получаем 5 * 2 = 10.
2. Функция возведения в квадрат: 25. Когда число 5 подставляется в эту функцию, мы получаем 5 * 5 = 25.
3. Функция вычитания трех: 2. Если в функцию подставить число 5, мы получим 5 - 3 = 2.
Таким образом, можем видеть, что значения простых функций от числа могут быть различными и зависят от конкретной функции, которую мы рассматриваем. Важно уметь правильно определить функцию и понять, какой результат она даст при подстановке конкретного числа.
Примеры сложных функций и их значения от числа

Функции могут быть очень разнообразными и сложными. Рассмотрим несколько примеров сложных функций и найдем их значения от определенного числа.
| Функция | Значение от числа 5 |
|---|---|
| f(x) = x^2 + 3x + 2 | f(5) = 5^2 + 3*5 + 2 = 25 + 15 + 2 = 42 |
| g(x) = sin(x) + cos(x) | g(5) = sin(5) + cos(5) ≈ -0.958924 + 0.283662 ≈ -0.675262 |
| h(x) = log(x) | h(5) = log(5) ≈ 1.60944 |
Как видим, значения функций от числа могут быть как целыми числами, так и десятичными. Знание математических функций и умение находить их значения позволяют решать различные задачи и применять их в различных областях науки и техники.