Нахождение значения функции при определенном значении x – одна из основных задач, которые возникают при изучении математики и аналитической геометрии. Особый интерес представляет собой нахождение значения функции при x, равном корню x. Это задача, требующая аккуратного решения и использования определенных приемов.
Для начала, необходимо понять, что такое корень x. Корень x – это такое значение переменной x, при котором функция обращается в ноль. Другими словами, если подставить это значение x в уравнение функции, получится ноль. Величина корня x может быть положительной, отрицательной или равной нулю.
Чтобы найти значение функции при x, равном корню x, нужно использовать следующую последовательность действий. Во-первых, необходимо выразить корень x через уравнение функции. Затем подставить это значение x в уравнение и решить его, чтобы получить значение функции.
Примером может служить функция y = x^2, где x – корень. Для начала, найдем значение корня, приравняв функцию к нулю: x^2 = 0. Из этого уравнения следует, что корень x равен нулю. Далее, подставляет это значение в исходное уравнение: y = (0)^2 = 0. Значит, при x, равном корню x, значение функции равно нулю.
Подготовка к поиску значения функции при x равном корню x

Перед тем, как приступить к нахождению значения функции при x равном корню x, необходимо выполнить несколько подготовительных шагов. В данном разделе мы рассмотрим эти шаги подробнее.
1. Определите функцию, в которой требуется найти значение при x, равном корню x. Убедитесь, что функция определена и имеет значение при данном значении.
2. Проверьте, существует ли корень x для данной функции. Для этого можете использовать методы анализа функций, такие как график функции, метод проб и ошибок или численные методы.
3. Если корень x существует, найдите его точное значение. Для этого можно воспользоваться методами аналитического решения уравнения или численными методами, такими как метод половинного деления или метод Ньютона.
4. Проверьте, что значение корня x соответствует допустимому диапазону значений для данной функции. Например, если функция имеет ограничение по x, убедитесь, что значение корня находится в этом ограничении.
5. Подставьте найденное значение корня x в функцию и вычислите значение функции при этом значении. Полученное значение будет ответом на задачу.
Если все предварительные шаги были выполнены корректно, вы сможете найти значение функции при x, равном корню x, с уверенностью и безошибочно.
Использование графика функции для определения значения при x равном корню x
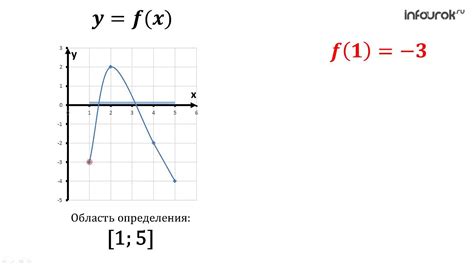
Чтобы использовать график функции для определения значения при x, равном корню x, необходимо следовать нескольким шагам:
- Постройте график функции f(x) на координатной плоскости. Подсказка: для детального изучения поведения функции вблизи корня x рекомендуется выбрать узкое окно по оси x.
- Найдите точку, в которой график функции пересекает ось x, то есть точку, в которой f(x) = 0.
- Определите значение функции при найденном корне x, используя график. Для этого можно прочитать значение f(x) на оси y в точке пересечения графика с осью x.
Учитывайте, что график функции - это лишь визуальный инструмент, и его использование требует некоторой оценки и приближения. Однако, данный метод может быть довольно эффективным для быстрого определения значений функции при x, равном корню x.
Применение численных методов для нахождения значения функции при x равном корню x

Численные методы предоставляют нам возможность приближенно найти значение функции, основываясь на вычислениях с конечным числом шагов. Для задачи нахождения значения функции при x равном корню x применяются различные алгоритмы, в том числе методы простой итерации и метод Ньютона.
Метод простой итерации основан на итерационном процессе, в котором начальное приближение значения функции заменяется на новое, полученное путем применения к нему определенной функции. Таким образом, мы последовательно приближаемся к искомому значению. Для этого метода необходимо иметь хорошо определенную функцию, сходящуюся в окрестности корня.
Метод Ньютона является более сложным и точным численным методом. Он основан на использовании аппроксимации функции с помощью касательной, проходящей через текущую точку. Далее, решается уравнение касательной для нахождения новой точки приближения. И таким образом, мы снова приближаемся к искомому значению функции.
При использовании любого численного метода для нахождения значения функции при x равном корню x, необходимо помнить о возможных проблемах с неправильным выбором начального приближения, а также о том, что некоторые функции могут не иметь корней или иметь несколько корней.
Использование специализированных онлайн-калькуляторов для поиска значения функции при x равном корню x

Если вам требуется найти значение функции при x, равном корню x, вы можете воспользоваться специализированными онлайн-калькуляторами. Они позволяют проводить вычисления и получать ответы с высокой точностью.
Такие калькуляторы обычно требуют ввода функции и значения переменной. В данном случае, чтобы найти значение функции при x равном корню x, необходимо ввести функцию f(x) = x и значение x = √x. Программа выполнит вычисления и выдаст результат.
Онлайн-калькуляторы также могут предоставить дополнительные функции, например, возможность построения графиков, расчета производной или интеграла функции. Это может быть полезно, если вам требуется дополнительная информация о функции, основанная на значении x = √x.
| Преимущества использования онлайн-калькуляторов: |
|---|
| 1. Быстрый и удобный способ решения математических задач; |
| 2. Высокая точность вычислений; |
| 3. Возможность проведения сложных математических операций; |
| 4. Возможность построения графиков и анализа функций. |
Использование специализированных онлайн-калькуляторов для поиска значения функции при x равном корню x может значительно упростить процесс и обеспечить точность результата.
Примеры решения задачи нахождения значения функции при x равном корню x

Найти значение функции при x, равном корню x, может быть немного сложнее, чем решение обычных задач. В данном разделе приведены несколько примеров, которые помогут вам разобраться с этим типом задачи.
Пример 1:
Дана функция f(x) = x^2 - 5x + 6. Найдем значение функции при x, равном корню x.
- Найдем корни уравнения: x^2 - 5x + 6 = 0.
- Решим уравнение: (x - 2)(x - 3) = 0. Получаем два корня: x1 = 2, x2 = 3.
- Подставим каждый из корней в исходную функцию: f(2) = 2^2 - 5*2 + 6 = 4 - 10 + 6 = 0, f(3) = 3^2 - 5*3 + 6 = 9 - 15 + 6 = 0.
- Таким образом, значение функции при x, равном корню x, равно 0.
Пример 2:
Дана функция f(x) = sqrt(x) - x. Найдем значение функции при x, равном корню x.
- Найдем корень уравнения: sqrt(x) - x = 0.
- Решим уравнение: sqrt(x) = x. Получаем корень x = 0.
- Подставим корень в исходную функцию: f(0) = sqrt(0) - 0 = 0 - 0 = 0.
- Таким образом, значение функции при x, равном корню x, равно 0.
Пример 3:
Дана функция f(x) = (x - 1)(x - 4). Найдем значение функции при x, равном корню x.
- Найдем корни уравнения: (x - 1)(x - 4) = 0.
- Решим уравнение: x - 1 = 0 или x - 4 = 0. Получаем два корня: x1 = 1, x2 = 4.
- Подставим каждый из корней в исходную функцию: f(1) = (1 - 1)(1 - 4) = 0*(-3) = 0, f(4) = (4 - 1)(4 - 4) = 3*0 = 0.
- Таким образом, значение функции при x, равном корню x, равно 0.
Надеемся, что приведенные примеры помогут вам лучше понять и научиться решать задачи нахождения значения функции при x, равном корню x. Не забывайте проверять результаты подстановкой и решать уравнения для нахождения корней. Удачи вам в решении задач!