Отыскать значение функции в конкретной точке имеет особое значение в математике. Оно может помочь нам понять, как ведет себя функция в определенной точке и какие значения она принимает в этой точке. В данной статье мы рассмотрим, как найти значение функции, когда аргумент равен нулю.
Для начала необходимо понять, что такое значение функции. Значение функции - это результат вычисления функции при определенном значении аргумента. Оно обозначается как f(x), где x - значение аргумента.
Если нужно найти значение функции в точке х нулевое, то это означает, что необходимо вычислить f(0), то есть подставить вместо х ноль. Например, если у нас есть функция f(x) = 2x + 3, то значение функции в точке х нулевое будет:
f(0) = 2 * 0 + 3 = 3.
Таким образом, значение функции в точке х нулевое равно трем. Точно так же можно вычислить значение функции в любой другой точке, подставляя ее вместо аргумента функции.
Определение функции и ее значения в разных точках
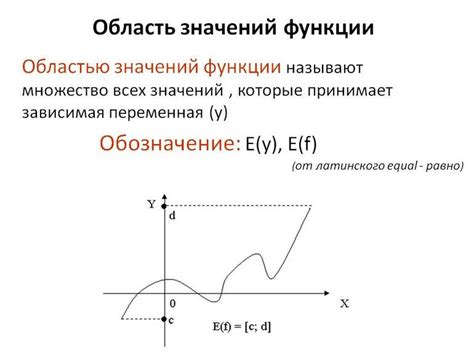
Значение функции в данной точке определяется подстановкой значения данной точки в уравнение или формулу, описывающую функцию. Результатом подстановки является число, которое и является значением функции в данной точке. Как правило, значение функции обозначается буквой y или f(x).
Найти значение функции в точке нулевое означает, что необходимо найти значение функции при подстановке нуля в качестве аргумента. Если результат подстановки равен нулю, тогда значение функции в точке х нулевое. В противном случае, значение функции не является нулевым.
Примеры:
1. Для функции f(x) = x^2 - 4x + 3:
Подставим x = 0:
f(0) = 0^2 - 4(0) + 3 = 0 - 0 + 3 = 3.
Значение функции в точке x = 0 равно 3.
2. Для функции g(x) = 2x - 5:
Подставим x = 0:
g(0) = 2(0) - 5 = -5.
Значение функции в точке x = 0 равно -5.
Таким образом, чтобы найти значение функции в точке х нулевое, необходимо подставить нуль в качестве аргумента и выполнить соответствующие арифметические операции.
Создание уравнения для нахождения значения функции в точке x=0
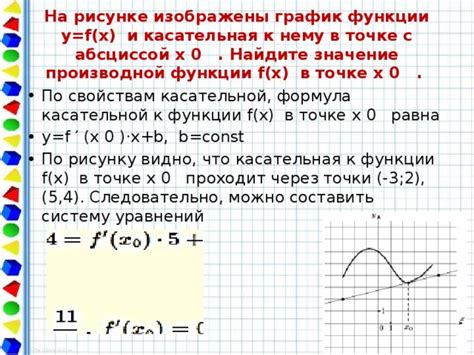
Для нахождения значения функции в точке x=0 необходимо создать и решить уравнение, в котором подставить значение x=0. Уравнение может быть дано в виде аналитической формулы, графика или таблицы значений функции.
Процесс создания уравнения зависит от типа функции. Рассмотрим несколько примеров:
Линейная функция: уравнение линейной функции имеет вид y = kx + b, где k - коэффициент наклона, b - свободный член. Для нахождения значения функции в точке x=0 необходимо подставить x=0 в уравнение: y = k(0) + b = b. Значение функции в точке x=0 равно свободному члену b.
Квадратичная функция: уравнение квадратичной функции имеет вид y = ax^2 + bx + c, где a, b, c - коэффициенты. Для нахождения значения функции в точке x=0 необходимо подставить x=0 в уравнение: y = a(0)^2 + b(0) + c = c. Значение функции в точке x=0 равно коэффициенту c.
Тригонометрическая функция: уравнение тригонометрической функции может иметь различные формы. Например, для синусоидальной функции вида y = A*sin(Bx + C) + D, где A, B, C, D - параметры, для нахождения значения функции в точке x=0 необходимо подставить x=0 в уравнение: y = A*sin(B(0) + C) + D = A*sin(C) + D. Значение функции в точке x=0 равно A*sin(C) + D.
Таким образом, для нахождения значения функции в точке x=0 необходимо определить тип функции и подставить x=0 в соответствующее уравнение функции. Такой подход позволяет получить точный результат.
Примеры вычисления значения функции в точке х нулевое
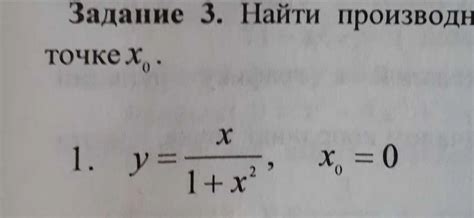
Рассмотрим несколько примеров вычисления значения функции в точке х нулевое:
- Функция f(x) = x^2 - 4
- Функция f(x) = sin(x)
- Функция f(x) = e^x - 1
Чтобы узнать, когда значение функции будет равно нулю, нам нужно решить уравнение x^2 - 4 = 0.
Решение данного уравнения: x^2 = 4, x = ±2
Значит, значения функции равны нулю в точках x = -2 и x = 2.
Функция синуса имеет периодичность 2π, то есть f(x + 2π) = f(x).
Значение функции будет равно нулю в точках, в которых sin(x) = 0.
Такие точки находятся при x = kπ, где k - целое число.
Например, функция равна нулю в точках x = 0, x = π, x = 2π и так далее.
Чтобы найти значения функции равные нулю, нужно решить уравнение e^x - 1 = 0.
Решение данного уравнения: e^x = 1, x = 0
Значение функции равно нулю только в точке x = 0.
Вычисление значения функции в точке х нулевое позволяет определить интересующие нас точки на графике функции, а также решить уравнения, исходя из условия равенства значения функции нулю.