Одной из основных задач математики является нахождение значения функции в заданной точке. Это может быть полезно в различных ситуациях, будь то уточнение результатов эксперимента или прогнозирование будущих значений. Однако, для решения этой задачи требуется понимание основных понятий и методов работы с функциями.
Первым шагом является определение функции, значение которой мы хотим найти. Функция представляет собой математическое правило, которое сопоставляет каждому элементу из одного множества (называемого областью определения) элемент из другого множества (называемого областью значений). Мы обозначаем функцию буквой, например, f(x).
Для нахождения значения функции в заданной точке, необходимо подставить эту точку вместо переменной (в данном случае, x) в правило функции. Затем мы выполняем все необходимые математические операции, чтобы получить конечный результат. Например, если у нас есть функция f(x) = 2x + 3, и мы хотим найти значение функции в точке x = 5, мы должны подставить 5 вместо x: f(5) = 2 * 5 + 3 = 13.
Важно помнить, что не все точки могут быть определены в функции. Существуют так называемые "недопустимые" значения, при которых функция не имеет значения. Например, если у нас есть функция g(x) = 1/x, то при x = 0 функция не определена, так как деление на ноль невозможно. Поэтому перед вычислением значения функции в заданной точке необходимо проверить, что эта точка принадлежит области определения функции.
Понятие математической функции
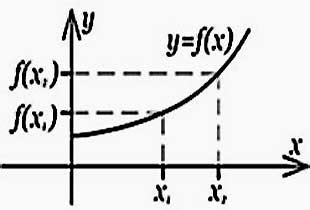
Математическая функция представляет собой правило, которое сопоставляет каждому элементу из одного множества, называемого областью определения функции, единственный элемент из другого множества, называемого областью значений функции.
Функция обычно обозначается символом f и записывается в виде f(x), где x - элемент из области определения функции. Значение функции в точке x, обозначается как f(x).
Математическая функция описывает зависимость между переменными или явлениями. Она может быть задана аналитически, графически или в виде таблицы.
Значение функции в заданной точке можно найти, подставив значение переменной x в функцию и вычислив результат. Это позволяет определить, какой результат дает функция при конкретных значениях переменных.
Определение значения функции в заданной точке

Для определения значения функции в заданной точке необходимо знать аналитическое выражение функции и значения аргументов.
Допустим, у нас есть функция f(x), где x - независимая переменная, а f - выражение функции. Нам нужно найти значение функции в заданной точке x = a.
Для этого нам нужно подставить значение a вместо переменной x в выражение функции f(x). В результате получим число, которое и будет значением функции в заданной точке.
Для наглядности можно построить таблицу, в которой будут перечислены значения x и соответствующие им значения функции f(x):
| Значение x | Значение f(x) |
|---|---|
| a | f(a) |
Таким образом, подставляя значение a вместо x в выражение функции f(x), мы получим значение функции в заданной точке.
Например, если у нас есть функция f(x) = 2x + 3, и мы хотим найти значение функции в точке x = 5, то подставляя x = 5 в выражение функции, получаем:
| Значение x | Значение f(x) |
|---|---|
| 5 | 2 * 5 + 3 = 13 |
Таким образом, значение функции f(x) в точке x = 5 равно 13.
Примеры функций и их значений в заданных точках
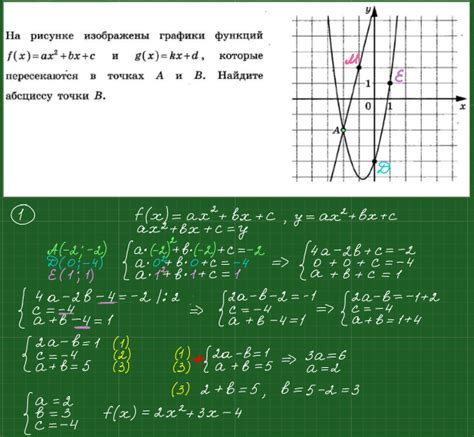
В математике функция представляет собой зависимость между входными и выходными значениями. Зная вид функции и задав определенную точку, мы можем найти значение функции в этой точке. В данной статье рассмотрим несколько примеров функций и вычислим их значения в заданных точках.
Пример 1: Квадратная функция
Рассмотрим функцию вида:
f(x) = x^2
Чтобы найти значение функции, подставим заданную точку вместо переменной x:
Пусть x = 3, тогда:
f(3) = 3^2 = 9
Таким образом, значение функции f(x) = x^2 в точке x = 3 равно 9.
Пример 2: Линейная функция
Рассмотрим функцию вида:
f(x) = 2x + 5
Подставим заданную точку:
Пусть x = -2, тогда:
f(-2) = 2 * (-2) + 5 = -4 + 5 = 1
Итак, значение функции f(x) = 2x + 5 в точке x = -2 равно 1.
Пример 3: Тригонометрическая функция
Рассмотрим функцию синус:
f(x) = sin(x)
Пусть x = π/2, тогда:
f(π/2) = sin(π/2) = 1
Значение функции f(x) = sin(x) в точке x = π/2 равно 1.
Таким образом, мы рассмотрели несколько примеров функций и вычислили их значения в заданных точках. Знание этих принципов поможет вам более полно изучить работу и свойства функций в математике.
Методы нахождения значения функции в заданной точке
1. Аналитический метод - это метод нахождения значения функции путем аналитических преобразований и подстановки значений аргументов. Этот метод имеет широкое применение в решении простых и сложных функциональных уравнений.
2. Графический метод - это метод нахождения значения функции путем построения графика функции и определения координаты точки на графике. Данный метод позволяет наглядно представить зависимость функции от аргумента.
3. Численные методы - это методы, основанные на приближенных вычислениях и численных алгоритмах. Существуют различные численные методы, такие как метод бисекции, метод Ньютона, метод секущих и другие, которые позволяют находить значение функции с заданной точностью.
4. Программные методы - это методы, которые используются в программах и компьютерных системах для нахождения значения функции. Такие методы могут быть реализованы на различных языках программирования и использоваться в математических пакетах для выполнения сложных вычислений.
Зависимо от конкретной задачи и условий, выбор метода нахождения значения функции в заданной точке может быть различным. Важно учитывать точность и эффективность выбранного метода, чтобы получить достоверные результаты и оптимальное решение.
Точность и округление значений функции
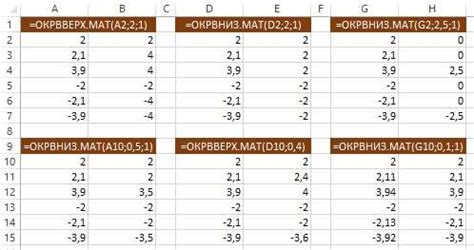
При нахождении значения функции в заданной точке важно обратить внимание на точность вычислений и корректное округление результата. Ошибки округления могут привести к неправильным результатам, особенно при работе с функциями, которые имеют комплексные числа или очень большие/маленькие значения.
Для обеспечения точности значений функции следует использовать подходящий алгоритм округления. В большинстве случаев наиболее подходящим является округление по правилам математического округления. Оно заключается в следующем: если дробная часть числа больше или равна 0.5, то число округляется в большую сторону, иначе - в меньшую сторону.
При выполнении вычислений со значениями функции также следует обратить внимание на точность самой функции. Некоторые функции могут иметь ограничения на допустимый диапазон значений аргумента или могут иметь особенности в определенных точках. Перед использованием функции рекомендуется ознакомиться с ее описанием и возможными ограничениями для получения корректных результатов.
Значение функции в экстремальных точках
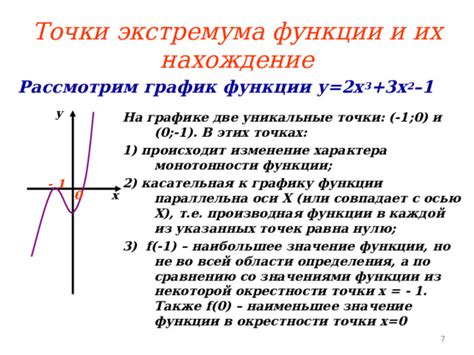
Чтобы найти значения функции в экстремальных точках, следует выполнить следующие шаги:
- Найти производную функции.
- Найти корни производной – это будут экстремальные точки.
- Проверить знаки производной функции до и после каждой экстремальной точки.
- Подставить найденные экстремальные точки в исходную функцию и найти соответствующие значения.
Результатом будет набор значений функции в экстремальных точках.
Зная значения функции в экстремальных точках, можно более точно оценить поведение функции в окрестностях этих точек и определить, какие значения функции достигаются в них.
1. Внимательно изучите задачу и убедитесь, что вы понимаете все условия и данные.
2. Определите, какая функция описывает заданную ситуацию. Если функция не задана явно, попробуйте выразить ее в явном виде или использовать алгоритмические методы для ее определения.
3. Подставьте заданную точку в функцию и рассчитайте значение. Будьте внимательны при выполнении математических операций и учете возможных ошибок.
4. Если функция сложная или требует большого объема вычислений, используйте компьютерные программы или калькуляторы для упрощения процесса.
5. Проверьте полученный результат на соответствие задаче и его логическую правдоподобность. При необходимости выполните дополнительные расчеты или проверки.
6. В случае использования научных инструментов или программного обеспечения, убедитесь в корректности настроек и введенных данных.
Следуя этим советам, вы сможете найти значение функции в заданной точке с большей точностью и уверенностью.