Прямоугольные треугольники - это одна из самых фундаментальных фигур в геометрии, а катет - одна из его главных составляющих. Как известно, прямоугольный треугольник имеет один прямой угол, равный 90 градусам. В этой статье мы рассмотрим, как найти длину катета через заданный угол, а также предоставим примеры для лучшего понимания.
Для начала вспомним основные формулы, связанные с прямоугольными треугольниками. Для нахождения длины катета a через заданный угол А, мы можем воспользоваться тангенсом этого угла. Тангенс представляет отношение длины противолежащего катета к длине прилежащего катета в прямоугольном треугольнике.
Формула для вычисления катета a через угол А выглядит следующим образом: a = b * tan(A), где b - длина другого катета. Не забудьте преобразовать угол из градусов в радианы, если ваш калькулятор работает с радианами. Например, если угол составляет 45 градусов, то его радианная мера будет равна (π/4).
Давайте рассмотрим пример. Предположим, у нас есть прямоугольный треугольник со сторонами a = 3 см и b = 4 см, а угол А составляет 30 градусов. Мы хотим найти длину катета a. Подставим значения в формулу: a = 4 * tan(30°). После вычислений, получаем, что a примерно равно 2,309 см.
Формулы для нахождения катета прямоугольного треугольника через угол
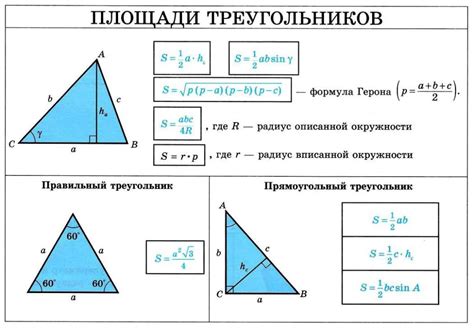
1. Формула синуса:
Катет = гипотенуза * sin(угол)
2. Формула косинуса:
Катет = гипотенуза * cos(угол)
3. Формула тангенса:
Катет = гипотенуза * tan(угол)
Гипотенуза – это наибольшая сторона треугольника, которая противоположна прямому углу. Используя одну из указанных формул, можно вычислить значение катета при известном угле и длине гипотенузы.
Например, если известно, что угол прямоугольного треугольника равен 45°, а длина гипотенузы равна 10, можно найти длину катета, используя формулу косинуса:
Катет = 10 * cos(45°) ≈ 7.07
Зная значения угла и гипотенузы, можно применить нужную формулу и получить значение катета для использования в решении математических задач.
Формула катета через синус угла
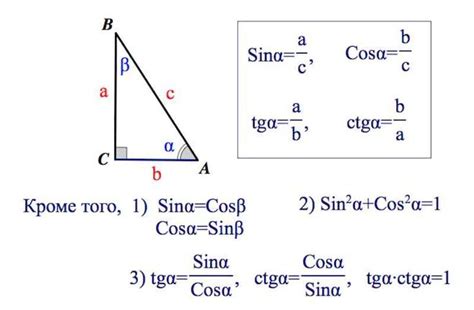
Формула катета через синус угла позволяет найти значение катета прямоугольного треугольника, если известен синус угла между этим катетом и гипотенузой.
Формула имеет вид:
| Катет | = | Гипотенуза | * | Синус угла |
Используя данную формулу, мы можем найти значение катета, зная длину гипотенузы и синус угла между катетом и гипотенузой.
Например, пусть у нас есть прямоугольный треугольник с гипотенузой длиной 10 и углом в 30 градусов. Мы можем использовать формулу катета через синус угла:
Катет = 10 * sin(30)
Катет = 10 * 0.5
Катет = 5
Таким образом, в данном примере значение катета равно 5.
Формула катета через тангенс угла
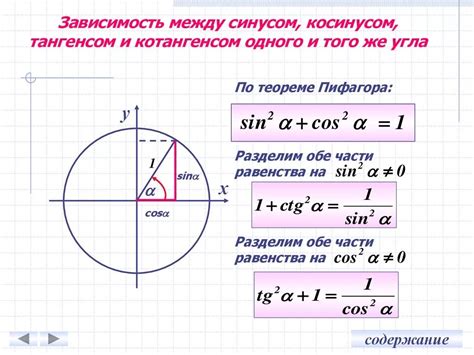
Для прямоугольного треугольника, где известен один из углов, можно использовать формулу для нахождения длины катета через тангенс этого угла.
Формула выглядит следующим образом:
- Тангенс угла равен отношению противолежащего катета к прилежащему катету:
тан α = a/b
- где α - измеряемый угол,
- a - длина противолежащего катета,
- b - длина прилежащего катета.
Для нахождения длины противолежащего катета нужно знать длину прилежащего катета и угол.
Пример:
Допустим, у нас есть прямоугольный треугольник ABC, где угол α равен 30 градусов, а длина прилежащего катета b равна 5 единицам. Чтобы найти длину противолежащего катета, мы можем использовать формулу:
- тан 30° = a/5
Чтобы найти значение a, мы умножаем обе стороны уравнения на 5, получаем:
- 5 * тан 30° = a
По таблице тангенсов углов, тангенс 30° равен примерно 0.5774. Вычисляя это значение, мы получаем:
- 5 * 0.5774 = a
Таким образом, длина противолежащего катета a составляет примерно 2.887 единицы.
Теперь мы знаем, что прилежащий катет равен 5 и угол α равен 30 градусов, а противолежащий катет равен примерно 2.887.
Примеры нахождения катета прямоугольного треугольника через угол
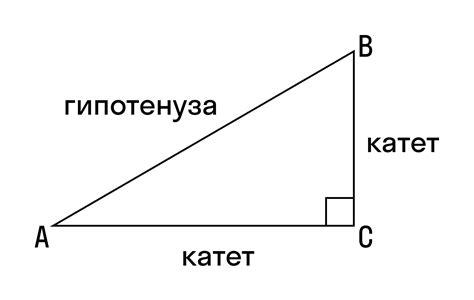
Найдем катет прямоугольного треугольника, если известен один из углов и длина гипотенузы.
Пример 1:
- Угол: 30 градусов;
- Гипотенуза: 10 см.
Для нахождения катета воспользуемся тригонометрическим соотношением: катет = гипотенуза * sin(угол).
Подставим известные значения: катет = 10 * sin(30).
Рассчитаем значение синуса угла 30 градусов: sin(30) ≈ 0,5.
Тогда катет равен: катет ≈ 10 * 0,5 = 5 см.
Ответ: катет прямоугольного треугольника равен 5 см.
Пример 2:
- Угол: 60 градусов;
- Гипотенуза: 8 м.
Используя тригонометрическое соотношение, найдем катет: катет = гипотенуза * sin(угол).
Подставим известные значения: катет = 8 * sin(60).
Рассчитаем значение синуса угла 60 градусов: sin(60) ≈ 0,87.
Тогда катет равен: катет ≈ 8 * 0,87 ≈ 6,96 м.
Ответ: катет прямоугольного треугольника примерно равен 6,96 м.
Пример 3:
- Угол: 45 градусов;
- Гипотенуза: 12 дм.
Применим тригонометрическое соотношение для нахождения катета: катет = гипотенуза * sin(угол).
Подставим известные значения: катет = 12 * sin(45).
Рассчитаем значение синуса угла 45 градусов: sin(45) ≈ 0,71.
Тогда катет равен: катет ≈ 12 * 0,71 ≈ 8,52 дм.
Ответ: катет прямоугольного треугольника примерно равен 8,52 дм.
В приведенных примерах мы использовали тригонометрию для нахождения катета прямоугольного треугольника через известный угол и гипотенузу. Зная эти значения и применяя соответствующую формулу, можно рассчитать длину катета. Это может быть полезно при решении различных геометрических задач и для построения треугольников.