Уравнения с неизвестными числами - это одна из самых интересных и захватывающих тем в математике. Особенно, когда они становятся доступны для учащихся начальных классов. Учиться решать уравнения совсем несложно, если знать несколько простых правил. В этой статье я расскажу, как найти значение неизвестного числа (икс) в уравнении 5 класса на примере нескольких задач.

Уравнение - это математическое выражение, в котором есть неизвестное число (в данном случае икс) и знак равенства. Наши задачи будут состоять из простых математических действий: сложение, вычитание, умножение, деление. Чтобы найти значение икса, нужно провести несколько операций, следуя определенным правилам.

Например, рассмотрим задачу:

2 * х + 8 = 16

Для начала проведем обратные действия: от выражения 8 отнимем 8, чтобы избавиться от постоянного члена справа. 2 * х = 8

Далее разделим обе части уравнения на коэффициент при иксе (в данном случае 2): х = 8 / 2

Итак, значение икса равно х = 4.

Таким образом, решив уравнение, мы нашли значение икса, которое удовлетворяет уравнению. По аналогии можно решить и другие задачи. Не забывайте, каждое уравнение имеет алгоритм решения, на который нужно ориентироваться, чтобы правильно найти значение икса. Успехов вам на математических уроках!

Методы решения уравнения 5 класс

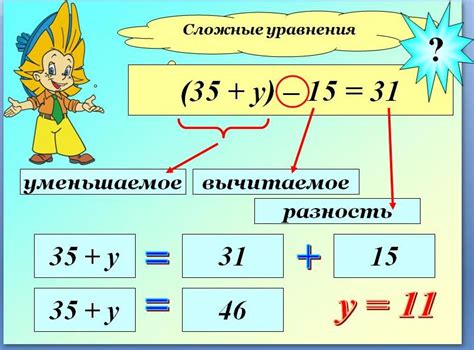
Решение уравнений в пятом классе может быть представлено несколькими методами, которые помогут найти значение переменной, обозначенной как "икс".

Один из наиболее простых методов - это метод подстановки. В этом методе мы подставляем различные значения "икс" в уравнение и проверяем, правильно ли оно срабатывает. Когда мы находим значение "икс", при котором уравнение выполняется, мы получаем ответ.

Другим распространенным методом является метод балансировки. Этот метод основан на идее сохранения баланса между двумя сторонами уравнения. Мы выполняем одни и те же операции с обеими сторонами уравнения, чтобы избавиться от переменной и найти ее значение.

Некоторые уравнения могут быть решены путем применения свойств арифметических операций, таких как сложение, вычитание, умножение и деление. Мы можем использовать эти свойства, чтобы перегруппировать термины и провести необходимые вычисления, чтобы найти значение "икс".

При решении уравнений в пятом классе важно помнить о законах алгебры и свойствах операций с числами. Это поможет нам с легкостью найти значение переменной и получить правильный ответ.

Простые уравнения: примеры и правила

Пример 1:

Решим уравнение: 3x + 5 = 17

Чтобы найти значение переменной x, нужно избавиться от числа, стоящего рядом с x, применив обратное действие. В данном случае, нужно избавиться от числа 5, прибавив к обеим сторонам уравнения -5:

3x + 5 - 5 = 17 - 5

3x = 12

Теперь нужно избавиться от коэффициента 3, чтобы получить x в одиночку. Для этого поделим обе стороны уравнения на 3:

3x/3 = 12/3

x = 4

Пример 2:

Решим уравнение: 2(2x - 3) = 10

Чтобы решить это уравнение, сначала выполним умножение: 4x - 6 = 10

Затем, как и в предыдущем примере, избавимся от числа -6, прибавив его к обеим сторонам уравнения:

4x - 6 + 6 = 10 + 6

4x = 16

Поделим обе стороны уравнения на 4, чтобы выразить переменную x:

4x/4 = 16/4

x = 4

Простые уравнения – это только начало. В дальнейшем вы встретите более сложные уравнения, но основные правила останутся прежними. Помните, что искомое значение переменной x можно найти, применяя обратные операции и постепенно избавляясь от чисел, до тех пор пока не получите одну переменную в одиночку. Удачи в решении уравнений!

Сложные уравнения: шаги и примеры

В математике существуют различные типы уравнений, и некоторые из них могут быть довольно сложными. Решение таких уравнений требует определенных шагов и стратегий. В этом разделе мы рассмотрим некоторые примеры сложных уравнений и покажем, как их решать.

Перед началом решения сложного уравнения важно задать себе вопрос: "Что нужно найти?". Для этого необходимо определить переменную, которую будем искать в уравнении. Обычно используется буква "х" для обозначения неизвестного значения.

Шаги решения сложного уравнения:

1. Попытайтесь упростить уравнение, удалив скобки или приведя подобные слагаемые.
2. Примените соответствующие свойства равенства и алгебраические операции, чтобы избавиться от переменных в одной части уравнения.
3. Для логических операций, таких как возведение в степень или извлечение квадратного корня, примените обратные операции для изолирования переменной.
4. Проверьте своё решение, подставив его обратно в исходное уравнение.

Пример сложного уравнения:

Решая сложные уравнения шаг за шагом, вы можете получить значение неизвестной переменной и определить, что является решением уравнения.

Практические примеры нахождения значения икс

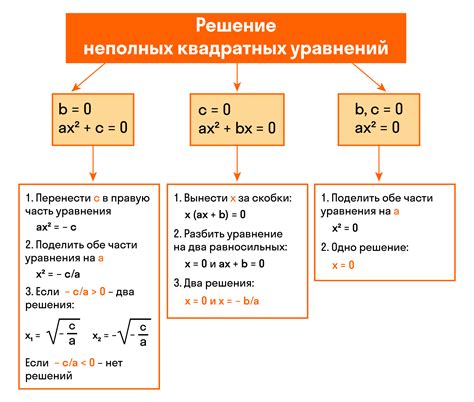
Для нахождения значения икс в уравнении требуется применить знания математики и элементарные арифметические операции. Давайте рассмотрим несколько практических примеров нахождения значения икс.

Пример 1:

• Уравнение: 2x + 5 = 11
• Для нахождения значения икс, нужно из обеих сторон уравнения вычесть число 5:
• 2x = 11 - 5
• 2x = 6
• Чтобы избавиться от коэффициента 2, нужно разделить обе части уравнения на 2:
• x = 6 ÷ 2
• x = 3

Ответ: значение икс равно 3.

Пример 2:

• Уравнение: 3(x + 2) = 18
• Для начала упростим выражение в скобках:
• x + 2 = 18 ÷ 3
• x + 2 = 6
• Чтобы найти значение икс, нужно из обеих сторон уравнения вычесть число 2:
• x = 6 - 2
• x = 4

Ответ: значение икс равно 4.

Пример 3:

• Уравнение: 4x - 7 = 9
• Для начала добавим 7 к обеим сторонам уравнения:
• 4x = 9 + 7
• 4x = 16
• Чтобы найти значение икс, нужно разделить обе стороны уравнения на 4:
• x = 16 ÷ 4
• x = 4

Ответ: значение икс равно 4.

Важно отметить, что при нахождении значения икс в уравнении нужно проводить одинаковые операции с обеими сторонами уравнения, чтобы сохранить равенство.