Как найти значение синуса при известных катетах прямоугольного треугольника — легкий способ для точных вычислений

Синус - это одно из основных тригонометрических отношений, которое показывает соотношение между отрезком противолежащим гипотенузе и гипотенузой прямоугольного треугольника. Если вам необходимо найти синус по катетам треугольника, вам понадобятся знания о функциях синуса и применение их при решении задач геометрии.

Для начала, следует найти гипотенузу прямоугольного треугольника, используя теорему Пифагора: сумма квадратов катетов равна квадрату гипотенузы. После этого, вам необходимо определить, какой из катетов является противолежащим гипотенузе, то есть находится напротив нужного угла.

Определение противолежащего катета поможет разобраться в том, какие измерения использовать для нахождения значения синуса. После этого, вы можете применить формулу синуса, которая гласит: синус угла равен отношению противолежащего катета к гипотенузе. Это поможет вам вычислить значение синуса для данного треугольника.

Определение катетов и гипотенузы

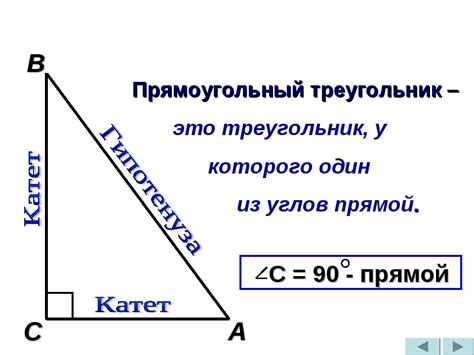
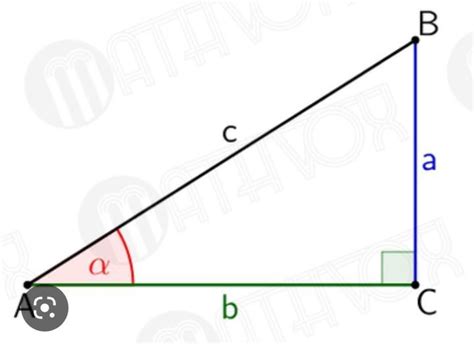
Катеты - это две стороны прямоугольного треугольника, которые вместе образуют прямой угол. Обозначаются буквами a и b.

Гипотенуза - это самая длинная сторона прямоугольного треугольника и лежит напротив прямого угла. Обозначается буквой c.

Катеты и гипотенуза прямоугольного треугольника связаны между собой теоремой Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Это выражается формулой:

c² = a² + b²

Используя эту формулу, можно рассчитать длину любого из катетов или гипотенузы, если известны длины двух других сторон. Такое знание особенно полезно при решении задач, связанных с прямоугольными треугольниками.

Формула нахождения синуса

Синус угла в прямоугольном треугольнике может быть найден с использованием соотношения между катетами и гипотенузой.

Формула нахождения синуса угла θ:

sin(θ) = (противолежащий катет) / (гипотенуза)

где:

θ - угол в треугольнике,

противолежащий катет - сторона прямоугольного треугольника, расположенная напротив данного угла,

гипотенуза - наибольшая сторона в прямоугольном треугольнике, которая является гипотенузой.

Используя данную формулу, можно вычислить значение синуса для любого угла в прямоугольном треугольнике, если известны значения катетов и гипотенузы.

Нахождение первого катета

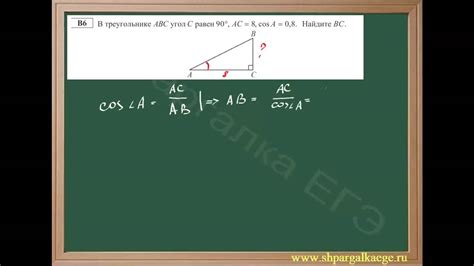
Чтобы найти первый катет прямоугольного треугольника, нужно знать длину второго катета и гипотенузы. Для этого можно воспользоваться формулой синуса:

синус угла = длина катета / длина гипотенузы

Выразив длину катета через синус угла и длину гипотенузы, получим:

длина катета = синус угла * длина гипотенузы

Итак, для нахождения первого катета прямоугольного треугольника нужно умножить синус нужного угла на длину гипотенузы.

Нахождение второго катета

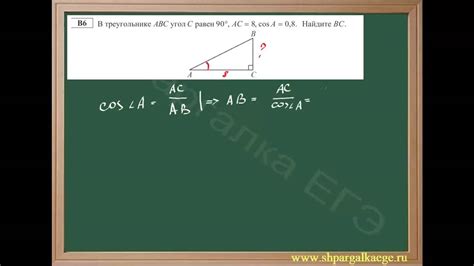
Для того чтобы найти второй катет прямоугольного треугольника, необходимо знать значение одного из катетов и гипотенузы.

Используя теорему Пифагора, можно записать следующее уравнение:

a² + b² = c²

Где a и b - это катеты, а c - гипотенуза треугольника.

Для нахождения второго катета, можно переписать уравнение следующим образом:

b² = c² - a²

Далее, извлекая квадратный корень из обеих частей уравнения, можно получить следующее:

b = √(c² - a²)

Таким образом, для нахождения второго катета необходимо извлечь квадратный корень из разности квадрата гипотенузы и квадрата известного катета.

Пример:

Допустим, известны катеты треугольника a = 3 и гипотенуза c = 5. Используя формулу, находим второй катет:

b = √(5² - 3²) = √(25 - 9) = √16 = 4

Таким образом, второй катет треугольника равен 4.

Примеры решения задач

Рассмотрим несколько примеров решения задач, связанных с нахождением синуса по катетам прямоугольного треугольника.

Пример 1:

Дан прямоугольный треугольник, у которого катеты равны a = 5 и b = 12. Необходимо найти значение синуса.

По определению синуса, sin(θ) = a / c, где θ - угол между гипотенузой и одним из катетов, c - гипотенуза. Таким образом, нам нужно найти значение гипотенузы, чтобы далее вычислить синус.

Используя теорему Пифагора (c^2 = a^2 + b^2), получаем c^2 = 5^2 + 12^2, откуда c = √(25 + 144) = √169 = 13.

Теперь можем вычислить синус: sin(θ) = a / c = 5 / 13 ≈ 0.3846.

Пример 2:

Рассмотрим прямоугольный треугольник, у которого катеты a = 4 и b = 3. Находим значение синуса.

Применяем аналогичные вычисления: c^2 = 4^2 + 3^2 = 16 + 9 = 25, следовательно, c = √25 = 5.

Тогда sin(θ) = a / c = 4 / 5 = 0.8.

Пример 3:

Пусть катеты прямоугольного треугольника равны a = 7 и b = 24. Необходимо найти значение синуса.

Используя теорему Пифагора, находим гипотенузу: c^2 = 7^2 + 24^2 = 49 + 576 = 625, следовательно, c = √625 = 25.

Тогда sin(θ) = a / c = 7 / 25 = 0.28.

Таким образом, с помощью теоремы Пифагора и определения синуса, мы можем находить значение синуса по заданным катетам прямоугольного треугольника.

Когда нельзя найти синус по катетам

Первый случай, когда найти синус нельзя, - когда один из катетов равен нулю или отрицательному числу. В таком случае, гипотенуза, которая является основанием для вычисления синуса, не существует.

Второй случай, когда найти синус невозможно, - когда длина одного из катетов превышает длину гипотенузы. В прямоугольном треугольнике гипотенуза всегда является самой длинной стороной. Если длина одного из катетов больше длины гипотенузы, то такого треугольника не существует и, соответственно, невозможно найти синус угла.

Таким образом, при решении задач на нахождение синуса по катетам прямоугольного треугольника необходимо учитывать эти ограничения и проверять, возможно ли найти синус в данной ситуации.

1. Для нахождения синуса по катетам прямоугольного треугольника необходимо поделить длину противоположного катета на гипотенузу.
2. Синус является одним из основных тригонометрических отношений, который позволяет определить соотношение между относительными длинами сторон треугольника и значениями его углов.
3. Синус имеет значения от -1 до 1, где -1 соответствует значение угла 270 градусов, а 1 – 90 градусов.
4. Синус можно выразить как отношение катета к гипотенузе, что позволяет определить его значение даже без прямоугольного треугольника.
5. Важно помнить, что для вычисления синуса по катетам прямоугольного треугольника необходимо знать значения катетов и гипотенузы, а также следовать формуле sin(θ) = противоположный катет / гипотенуза.

Понимание тригонометрических отношений, включая синус, позволяет решать различные задачи, связанные с геометрией и физикой, а также применять их в различных научных и технических областях.