Единичная окружность - это окружность радиусом равным единице. Угол, образованный двумя лучами, начинающимися в центре окружности и заканчивающимися на окружности, может быть измерен в радианах. Важно уметь находить значение синуса угла на единичной окружности, так как это позволяет решать задачи из различных областей математики и физики.
Для нахождения синуса угла на единичной окружности необходимо провести перпендикуляр из точки пересечения окружности с лучом на ось y. Затем, измерить длину этого перпендикуляра и разделить его на радиус окружности. Полученное значение будет равно синусу данного угла.
В математике синус обозначается как sin, и имеет широкое применение. Синус используется для решения геометрических задач, для анализа колебаний, для расчета треугольников и так далее. Понимание того, как найти синус угла на единичной окружности, является важным знанием для математиков, физиков, инженеров и других профессионалов, работающих с числами и формулами.
Значение синуса на единичной окружности
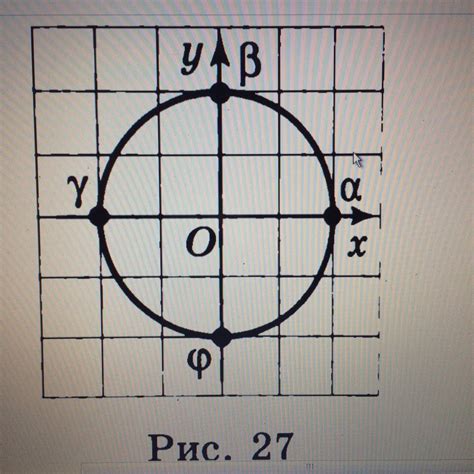
Синус угла на единичной окружности - это значение y-координаты точки P на окружности, образованной углом α между положительным направлением оси Ox и радиусом, проведенным из начала координат (точки O) до точки P.
Значение синуса на единичной окружности можно определить следующим образом:
- Постройте единичную окружность, центр которой находится в начале координат (0,0).
- Выберите угол α, измеренный против часовой стрелки от положительной оси Ox до радиуса P.
- Найти точку P на окружности, образованную углом α.
- Измерьте y-координату точки P.
- Значение y-координаты точки P будет являться значением синуса угла α на единичной окружности.
Значение синуса на единичной окружности будет изменяться от -1 до 1. Отрицательные значения синуса соответствуют углам, находящимся ниже оси Ox, а положительные значения - углам выше оси Ox.
Пример:
Допустим, у нас есть угол α, равный 45 градусов. Найдем его синус на единичной окружности:
- Построим единичную окружность.
- Измерим угол α, равный 45 градусов.
- Найдем точку P на окружности, образованной углом 45 градусов.
- Измерим y-координату точки P, которая будет равна √2 / 2.
Таким образом, синус угла 45 градусов на единичной окружности равен √2 / 2, что примерно равно 0.7071.
Знание значений синуса на единичной окружности позволяет решать различные задачи и вычислять значения синуса для других углов с помощью тригонометрических формул и связей.
Что такое синус?
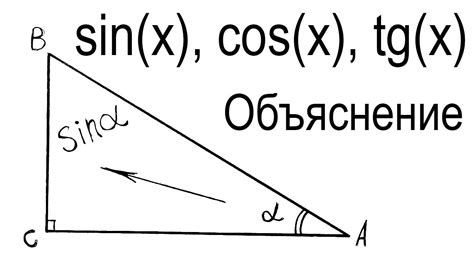
Таким образом, синус угла на единичной окружности является вертикальной координатой точки пересечения радиуса окружности с прямой, проходящей через центр окружности и образующей заданный угол с положительным направлением оси абсцисс. Он может принимать значения от -1 до 1, где положительные значения соответствуют углам, находящимся в верхней полуокружности, а отрицательные значения – в нижней полуокружности.
Используя синус, можно решать различные задачи, связанные с треугольниками и окружностями. Он является одной из основных функций в тригонометрии и широко применяется в науке, технике и других областях знания.
Свойства синуса
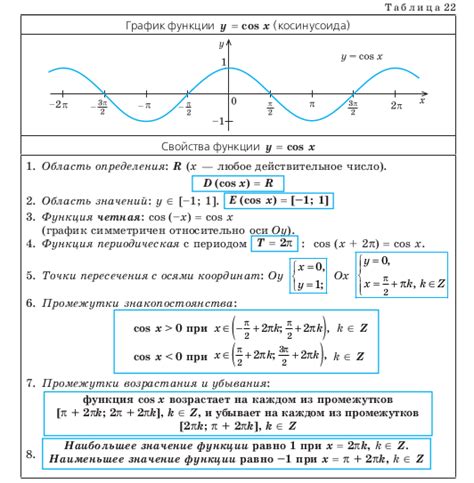
Синус (sin) угла на единичной окружности имеет несколько свойств, которые позволяют его использовать для различных математических расчетов и приложений:
| Свойство | Описание |
|---|---|
| Периодичность | Синус функции периодичен и повторяет свои значения каждые 2π радианы или 360 градусов. То есть sin(x) = sin(x + 2π) = sin(x + 360°). |
| Ограниченность | Значение синуса на единичной окружности всегда находится в пределах от -1 до 1. То есть -1 ≤ sin(x) ≤ 1 для любого угла x. |
| Симметричность | Синус функции является нечетной функцией, что означает, что sin(-x) = -sin(x). То есть симметричность синуса относительно оси ординат. |
| Геометрическое представление | Значение синуса угла на единичной окружности соответствует ординате точки на окружности, образованной этим углом. |
| Тригонометрические связи | Синус угла связан с другими тригонометрическими функциями, такими как косинус, тангенс и котангенс, с помощью соответствующих тригонометрических соотношений. |
Понимание этих свойств позволяет легко выполнять вычисления, анализировать углы и применять тригонометрические функции в различных областях, включая физику, инженерные расчеты, компьютерную графику и другие.
Окружность и синус
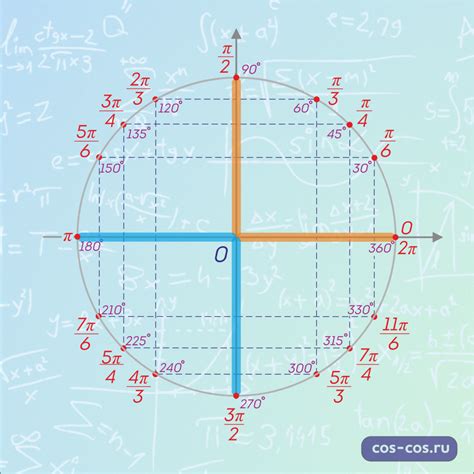
Синус угла - это одно из базовых тригонометрических отношений, определенных в прямоугольном треугольнике. Для единичной окружности, которая имеет радиус равный 1, синус угла определяется как y-координата точки на окружности, образующей данный угол с положительным направлением оси x.
Чтобы найти синус угла на единичной окружности, нужно:
- Построить единичную окружность с центром в начале координат (0, 0).
- Выбрать точку на окружности, которая образует данный угол с положительным направлением оси x.
- Определить y-координату этой точки.
- Эта y-координата будет являться значением синуса данного угла.
Например, если угол составляет 30 градусов, то точка на окружности будет иметь координаты (cos(30°), sin(30°)) = (0.87, 0.5). Значение синуса 30 градусов равно 0.5.
Единичная окружность
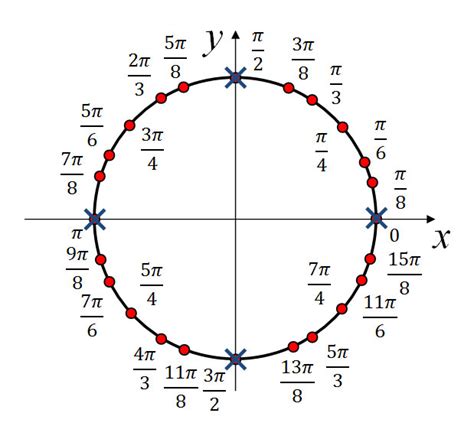
Единичная окружность можно представить с помощью тригонометрической функции синус. Для этого необходимо организовать координатную сетку и нанести на нее точки, лежащие на окружности в соответствии с их значением синуса. Таким образом, можно создать таблицу, в которой будут указаны значения угла, соответствующего точкам на единичной окружности, и их синусы.
| Угол (в радианах) | Значение синуса |
|---|---|
| 0 | 0 |
| π/6 | 1/2 |
| π/4 | √2/2 |
| π/3 | √3/2 |
| π/2 | 1 |
Из таблицы видно, что значения синуса изменяются от 0 до 1 в зависимости от угла, который составляет луч, исходящий из начала координат, с осью x. Таким образом, зная угол, можно вычислить значение синуса этого угла на единичной окружности.
Нахождение синуса угла на единичной окружности

Для того чтобы найти синус угла, необходимо провести луч из начала координат (точка O) до точки на окружности, которая соответствует заданному углу. Затем, проведя перпендикуляр из этой точки (точка P) до оси OX, мы получаем прямоугольный треугольник OPQ.
| Треугольник OPQ | |
|---|---|
| Сторона | Длина |
| OQ | 1 |
| OP | sin α |
| PQ | cos α |
Таким образом, можно сказать, что синус угла α равен длине отрезка OP. Исходя из этого, можно составить формулу для нахождения синуса угла:
sin α = OP
Зная, что радиус единичной окружности равен 1, можно утверждать, что:
OQ = 1
cos α = OQ = 1
sin α = OP
Таким образом, синус угла на единичной окружности равен длине отрезка, проведенного из начала координат до точки на окружности, которая соответствует заданному углу.
Примеры вычисления синуса на единичной окружности
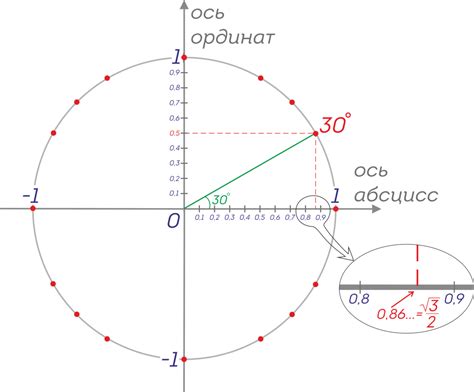
Рассмотрим несколько примеров вычисления синуса углов на единичной окружности.
Пример 1:
Для угла 30 градусов (или π/6 радиан) синус равен половине катета, противолежащего этому углу, то есть sin(30°) = 1/2.
Пример 2:
Для угла 45 градусов (или π/4 радиан) синус равен 1/√2, так как в прямоугольном треугольнике катеты равны, следовательно sin(45°) = 1/√2.
Пример 3:
Для угла 60 градусов (или π/3 радиан) синус равен √3/2, поскольку в равностороннем треугольнике высота, проведенная из вершины угла 60°, делит основание на две равные части, а теорема Пифагора дает возможность посчитать высоту и основание треугольника, откуда и найдем sin(60°) = √3/2.
Это лишь некоторые примеры, но с помощью схем и основных тригонометрических соотношений можно вычислить значения синуса для любого угла на единичной окружности.
