Степень числа – это операция, которая позволяет умножить число само на себя заданное количество раз. В школьной программе 6 класса особое внимание уделяется степеням чисел. Изучение степеней чисел позволяет упростить большие числа и выполнить сложные математические операции. Особый интерес представляет нахождение значения степени для рациональных чисел. В этой статье мы рассмотрим, как найти значение степени для чисел из класса рациональных чисел.
Рациональные числа – это числовая система, которая включает в себя все числа, которые можно представить в виде отношения двух целых чисел. Например, дроби, целые числа и десятичные дроби – все это рациональные числа. Важно понимать, что рациональные числа можно представить в виде конечной или периодической десятичной дроби.
Для нахождения значения степени рационального числа нужно возвести числитель и знаменатель в эту степень отдельно. Например, чтобы найти значение степени дроби 2/3 возводим числитель 2 в эту степень (в данном случае 2 в первую степень равно 2) и знаменатель 3 в эту степень (в данном случае 3 в первую степень равно 3). Таким образом, значение степени дроби 2/3 равно 2/3.
Что такое степень в математике?
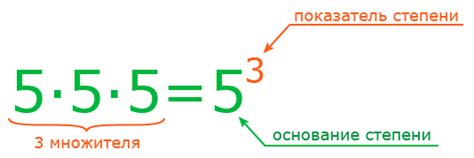
Основание степени - это число, которое возводится в степень. Показатель степени - это число, которое указывает, сколько раз основание должно быть умножено на себя. Например, в степени 2, основанием будет число 2, а показателем степени будет число 2.
Степень может быть положительной, отрицательной или нулевой. Положительная степень означает, что основание будет умножаться на себя заданное количество раз. Отрицательная степень означает, что основание будет делиться на само себя заданное количество раз. Степень равная нулю означает, что результатом будет единица.
В математике степени имеют много применений. Например, они позволяют быстро вычислять большие числа, описывать процессы роста и распада, моделировать сложные явления и многое другое.
Степень в математике: определение и основные понятия

Показатель степени может быть как натуральным числом, так и целым числом, рациональным числом или даже дробным числом. Показатель степени определяет, сколько раз нужно умножить основание на само себя.
Если показатель степени положительный, то результатом степени будет число, умноженное само на себя столько раз, сколько указано в показателе. Например, 2^3 = 2 * 2 * 2 = 8.
Если же показатель степени отрицательный, то результатом степени будет обратное значение основания, возведенное в положительную степень. Например, 2^-3 = 1 / (2^3) = 1 / 8 = 0.125.
Кроме того, степень может быть нулевой. В этом случае результатом будет всегда единица, вне зависимости от значения основания. Например, 2^0 = 1, 3^0 = 1, а любое число, отличное от нуля, возводимое в нулевую степень, также равно 1.
Рациональные числа - это числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами. Они могут быть положительными, отрицательными или нулевыми. Рациональные числа могут быть как конечными, так и периодическими десятичными дробями.
Таким образом, чтобы найти значение степени рационального числа, необходимо применить определение и правила степени математики в соответствии с данным показателем степени и основанием.
Значение степени в шестом классе
В 6 классе основной упор делается на степени с целым положительным показателем. Для нахождения значения степени нужно умножить число на себя столько раз, сколько указано в показателе. Например, чтобы найти значение степени 2^4 (2 в 4-й степени), нужно умножить число 2 на себя 4 раза:
- 2^4 = 2 * 2 * 2 * 2 = 16
Также стоит знать, что при умножении числа на само себя, можно добавить короткую запись с помощью знака умножения. Например, 2^4 можно записать как 24.
Помимо положительных степеней, в 6 классе также изучают отрицательные степени. Например, чтобы найти значение степени 2^(-3) (2 в -3-й степени), нужно сначала взять обратное значение числа (1/2) и умножить его на само себя 3 раза:
- 2^(-3) = (1/2) * (1/2) * (1/2) = 1/8
Итак, в 6 классе дети изучают значения степеней с положительными и отрицательными показателями. Это важные навыки, которые понадобятся в дальнейшем изучении математики.
Что нужно знать о значении степени в шестом классе
В степени рационального числа имеется две составные части: основание и показатель. Основание - это число, которое возводится в степень, а показатель - это число, которое указывает, сколько раз нужно умножить основание на себя.
Для простоты понимания, работайте со степенями положительных рациональных чисел. Например, чтобы найти значение степени 3 второй степени (3²), нужно умножить число 3 на само себя: 3² = 3 * 3 = 9.
Таблица ниже поможет вам лучше понять, как работает значение степени рациональных чисел:
| Показатель | Основание | Значение степени |
|---|---|---|
| 0 | Любое число, кроме 0 | 1 |
| 1 | Любое число | Основание |
| 2 | Любое число | Основание, умноженное на само себя |
Помните, что при умножении двух степеней с одинаковым основанием, показатель суммируется: aⁿ * aᵐ = a^(ⁿ⁺ᵐ).
Значение степени применимо ко многим математическим операциям, таким как сложение, вычитание и умножение. Изучение этой темы поможет вам развить навыки работы с числами и улучшить понимание математических концепций.
Где найти значения степени рациональных чисел для шестого класса

Значения степени рациональных чисел можно найти в учебниках по математике для шестого класса. Такие учебники содержат теоретический материал и примеры решения задач по данной теме.
Важно обратить внимание на следующие источники:
- Учебник по математике для шестого класса, рекомендованный Министерством образования. В нем можно найти раздел, посвященный степеням рациональных чисел, с объяснениями и примерами.
- Электронные учебники, доступные для скачивания или онлайн-чтения. В интернете существуют различные платформы, где ученик может найти учебники на разные темы, включая степени рациональных чисел.
- Дополнительные учебники и пособия, которые можно найти в библиотеке школы или городской библиотеке. В них обычно есть более подробное объяснение темы и больше примеров задач.
- Интерактивные обучающие ресурсы, которые подходят для самостоятельного изучения. Существуют сайты и приложения с интерактивными заданиями и уроками по математике, которые помогут закрепить знания о степенях рациональных чисел.
Выбирайте источник, который наиболее соответствует вашим предпочтениям и уровню знаний. Регулярное изучение теории и решение практических задач поможет вам лучше понять и применять степени рациональных чисел в учебе и повседневной жизни.
Как найти значение степени рациональных чисел?
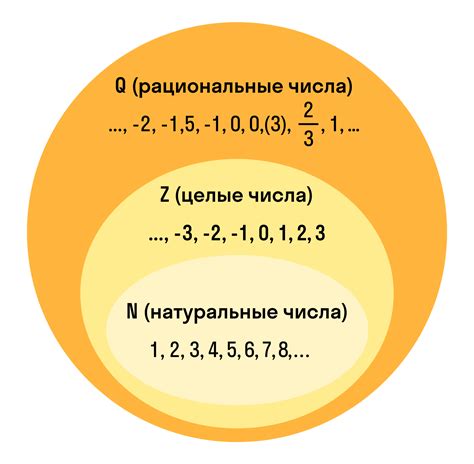
Для возведения рационального числа в степень, нужно возвести числитель и знаменатель в эту степень отдельно. Затем результирующие значения числителя и знаменателя нужно поделить между собой, чтобы получить окончательный результат.
Например, для того чтобы найти значение числа 3/4 в степени 2, нужно возвести числитель и знаменатель во вторую степень:
| Числитель | Знаменатель | Числитель^2 | Знаменатель^2 |
|---|---|---|---|
| 3 | 4 | 9 | 16 |
После возведения числителя и знаменателя во вторую степень, получаем значения 9 и 16 соответственно. Затем делим 9 на 16:
3/4 в степени 2 = 9/16
Таким образом, значение числа 3/4 во второй степени равно 9/16.
Аналогичным образом можно найти значение степени для любого рационального числа, зная его числитель и знаменатель.