Выражения с корнями являются одной из основных тем изучения алгебры в восьмом классе. Корни позволяют нам решать уравнения, находить значения выражений и проводить многочисленные вычисления. Изучение этой темы поможет вам развить навыки алгебраического мышления и применить их на практике.
В данном руководстве вы узнаете, как находить значения выражений с корнями, используя различные методы и приемы. Мы рассмотрим различные типы корней, такие как квадратный корень, кубический корень и другие, и научимся применять соответствующие формулы для их вычисления.
Вы также узнаете о свойствах корней и способах упрощения выражений с корнями. Это поможет вам более эффективно выполнять сложные алгебраические операции и упрощать выражения до более компактного и понятного вида.
Определение понятия "корень"

В математике понятие "корень" относится к числам, которые возведены в некоторую степень и дают определенное значение. Корень обратен показателю степени, то есть если число возведено в степень, то корнем этого числа будет другое число, которое при возведении в указанную степень даст изначальное число.
Корни применяются для решения уравнений и нахождения значений выражений. Часто в задачах по алгебре встречаются квадратные корни, обозначаемые знаком √. Например, квадратный корень из числа 4 равен 2, так как 2 × 2 = 4.
Корни могут быть радикалами, которые остаются без изменений. Например, радикалом числа 5 является √5.
Кроме квадратных корней, существуют кубические корни, четвертные корни и так далее. Корни могут быть действительными или комплексными, в зависимости от значения подкоренного выражения.
Операции с корнями включают извлечение корня из числа и возведение в степень. Знание свойств корней поможет нам успешно решать уравнения и выполнять вычисления.
| Термин | Определение |
| Корень | Число, возведенное в некоторую степень и давшее изначальное число |
| Квадратный корень | Корень, обозначаемый знаком √ и равный числу, при возведении в квадрат которого получается изначальное число |
| Свойства корней | Знания о правилах, которые позволяют совершать операции с корнями, такие как извлечение корня из числа и возведение в степень |
Корень в алгебре: основные определения

Основные определения, связанные с корнем:
| Термин | Определение |
|---|---|
| Радикал | Математический символ √, используется для обозначения корня. Например, √16 - корень из 16. |
| Индекс корня | Степень, в которую нужно возвести корень, чтобы получить исходное число. Например, индекс корня в выражении √216 равен 2. |
| Рациональный корень | Корень, который может быть выражен дробью (рациональным числом). Например, √4 = 2, так как 22 = 4. |
| Иррациональный корень | Корень, который не может быть выражен дробью (рациональным числом). Например, √2. |
Знание основных определений корня в алгебре поможет уточнить понимание и решать задачи, связанные с вычислением и использованием корней в алгебре.
Как найти корни выражения

Для нахождения корней выражения необходимо выполнить ряд шагов. Важно следовать им последовательно:
- Раскрыть скобки и выполнить все операции внутри них.
- Упростить выражение, сократив все возможные слагаемые и множители.
- Привести выражение к каноническому виду и записать его в виде многочлена.
- Решить получившийся многочлен.
- Проверить найденные корни, подставив их обратно в исходное выражение.
Для решения многочлена можно воспользоваться различными методами, такими как:
- Метод группировки коэффициентов.
- Метод синтетического деления.
- Метод подстановки.
- Метод сравнения коэффициентов.
При использовании данных методов необходимо помнить, что корни многочлена могут быть как действительными, так и комплексными числами.
Проверка корней предоставляет возможность убедиться в правильности решения. Для этого необходимо подставить найденные значения обратно в исходное выражение и проверить справедливость равенства.
Таким образом, нахождение корней выражения требует последовательного выполнения необходимых шагов и использования соответствующих методов решения многочлена.
Примеры задач на нахождение корней

Для решения задач по нахождению корней выражений необходимо использовать знания о различных методах решения квадратных и линейных уравнений. Вот несколько примеров задач:
- Найдите все корни уравнения x^2 - 4x + 4 = 0.
- Найдите все корни уравнения 2x^2 - 5x + 2 = 0.
- Найдите все корни уравнения 3x + 6 = 0.
Решение: Для решения данного уравнения мы можем воспользоваться формулой дискриминанта. Из формулы дискриминанта мы получаем, что D = b^2 - 4ac. В данном случае a = 1, b = -4 и c = 4. Подставив значения в формулу, получим D = (-4)^2 - 4 \cdot 1 \cdot 4 = 16 - 16 = 0. Так как дискриминант равен нулю, то уравнение имеет один корень. Далее, используем формулу для нахождения корня: x = \frac{-b}{2a}. Подставляя значения, получаем x = \frac{-(-4)}{2 \cdot 1} = \frac{4}{2} = 2. Таким образом, уравнение имеет один корень x = 2.
Решение: Для решения данного уравнения можно воспользоваться методом разложения на множители. Для этого нужно разложить многочлен на два множителя и приравнять каждый из множителей к нулю. Исходное уравнение 2x^2 - 5x + 2 = 0 можно представить в виде (2x - 1)(x - 2) = 0. Таким образом, получаем два уравнения: 2x - 1 = 0 и x - 2 = 0. Решив каждое из них, получим два корня: x = \frac{1}{2} и x = 2.
Решение: Для решения данного уравнения можно просто избавиться от константы и получить значение переменной x. В данном случае у нас есть одно уравнение: 3x + 6 = 0. Чтобы избавиться от константы, нужно вычесть 6 из обеих частей уравнения: 3x = -6. Затем, чтобы найти значение переменной x, нужно разделить обе части уравнения на 3: x = \frac{-6}{3} = -2. Таким образом, уравнение имеет один корень x = -2.
Методы решения выражений с корнями

Выражения с корнями можно решать с помощью различных методов, которые позволяют найти значения таких выражений. Рассмотрим некоторые из них:
1. Прямой подстановки
Самым простым методом является прямая подстановка значений корней в выражение. Например, если дано выражение √a + √b, а значения a и b равны 4 и 9 соответственно, то результатом будет 2 + 3 = 5.
2. Использование формулы суммы корней
Для выражений, в которых присутствует сумма или разность корней, можно использовать формулу суммы корней. Например, для выражения √a + √b можно использовать формулу a + 2√ab + b.
3. Метод рационализации знаменателей
Если в выражении имеется знаменатель, содержащий под корнем, то его можно рационализировать, умножив и числитель, и знаменатель на конгруэнтные множители. Например, для выражения 1 / (√a + √b) можно умножить числитель и знаменатель на (√a - √b) и получить результат (√a - √b) / (a - b).
Однако, необходимо помнить, что при решении выражений с корнями всегда необходимо проверять полученный результат, так как некоторые операции с корнями могут привести к появлению комплексных чисел или некорректным значениям.
Используя эти методы, можно решать различные задачи, связанные с выражениями с корнями, и находить значения таких выражений.
Квадратные уравнения: что это и как их решать
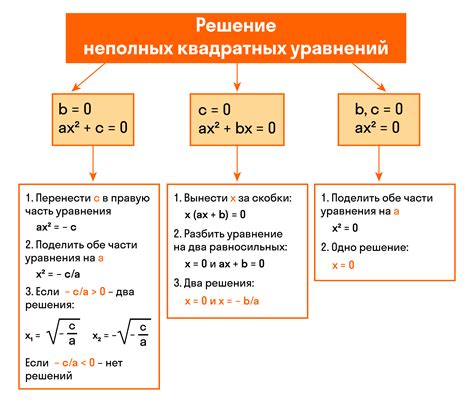
Решение квадратных уравнений может помочь нам найти значения переменной x, при которых уравнение выполняется. Обычно у нас есть два решения для квадратного уравнения. Эти решения могут быть действительными или комплексными числами.
Существуют различные методы для решения квадратных уравнений. Один из самых распространенных методов – это использование формулы квадратного корня.
Формула квадратного корня гласит:
x = (-b ± √(b2 - 4ac)) / 2a
Здесь ± означает, что у нас два возможных решения: одно с плюсом и одно с минусом. Действительные решения с плюсом и минусом соответственно называются корнями квадратного уравнения.
Чтобы найти корни квадратного уравнения, нам нужно знать значения коэффициентов a, b и c. Мы можем подставить эти значения в формулу и вычислить корни уравнения.
Помимо формулы квадратного корня, есть и другие методы для решения квадратных уравнений, такие как метод графиков, завершение квадрата и факторизация. Используя эти методы, мы можем найти корни квадратного уравнения и решить его.
Как получить значения выражения при заданном значении корня

Для нахождения значения выражения при заданном значении корня сначала нужно подставить это значение в выражение, а затем выполнить необходимые математические операции.
Пусть дано выражение:
Выражение: a * x + b
где a и b - коэффициенты, x - значение корня.
Для нахождения значения выражения при заданном значении корня необходимо:
- Заменить в выражении переменную x значением корня. То есть, вместо x подставить заданное значение.
- Выполнить математические операции: умножение, сложение.
Пример:
Заданное значение корня: x = 3
Выражение: 2 * x + 4
Подставим значение корня в выражение:
Выражение с подставленным значением корня: 2 * 3 + 4
Выполним математические операции:
2 * 3 = 6
6 + 4 = 10
Получаем, что значение выражения при заданном значении корня x = 3 равно 10.
Таким образом, чтобы получить значение выражения при заданном значении корня, нужно заменить переменную в выражении значением корня и выполнить необходимые математические операции.
Сложные выражения с корнями: алгоритм решения

Решение сложных выражений с корнями требует применения некоторых алгоритмов и методов, которые помогут нам упростить задачу и найти итоговое значение.
1. Начнем с вычисления отдельных корней в выражении. Для этого выражение необходимо разбить на отдельные корни и решить каждый из них отдельно.
2. Затем следует привести подобные корни вместе и объединить их в один корень, используя соответствующие правила. Например, корень sqrt(3) + sqrt(3) может быть упрощен до sqrt(6), так как корень второй степени из суммы корней равен корню из произведения корней.
3. После этого мы можем упростить любые еще существующие корни, применяя правила работы с корнями. Например, можно упростить корень из числа, умноженного на другой корень, заменив его на корень из их произведения и так далее.
4. После всех этих упрощений можно перейти к сложению и вычитанию выражений с корнями. Для этого необходимо привести все слагаемые к общему знаменателю, упростить их при необходимости и выполнить требуемую операцию.
5. Наконец, когда все выражения сложены или вычтены, можно перейти к умножению и делению. Для этого необходимо перемножить числитель и знаменатель фракции и упростить при необходимости.
Таким образом, для решения сложных выражений с корнями необходимо последовательно применять правила работы с корнями и упрощать выражения до тех пор, пока не получим окончательный результат.
Задачи из жизни, где необходимо использовать корни

Расчет площади поля
Представим себе ситуацию, когда нам необходимо выяснить площадь прямоугольного поля. Мы знаем, что его одна сторона равна 10 метров, а другая сторона неизвестная. Нам необходимо найти значение этой стороны, чтобы получить точные данные о площади. Для решения этой задачи мы можем использовать корни.
Пусть x - неизвестная сторона. Тогда площадь поля будет равна:
S = 10 * x = 10x
Зная, что площадь поля равна 100 квадратных метров, мы можем записать уравнение:
10x = 100
Для нахождения значения x, мы можем применить операцию извлечения корня:
x = √(100/10) = √10 ≈ 3.16
Таким образом, одна из сторон прямоугольного поля равна примерно 3.16 метра.
Расчет времени путешествия
Предположим, что мы планируем путешествие на поезде. Мы знаем, что скорость поезда составляет 80 км/ч, а расстояние, которое мы собираемся преодолеть, равно 320 км. Нам необходимо выяснить, сколько времени займет наше путешествие, чтобы спланировать свое время. В этой задаче мы также можем использовать корни.
Пусть t - время путешествия. Тогда расстояние можно выразить как:
s = v * t
Где v - скорость поезда.
Подставив значения, получим:
320 = 80 * t
Чтобы найти значение t, мы можем применить операцию извлечения корня:
t = √(320/80) = √4 = 2
Таким образом, путешествие займет 2 часа.
Расчет объема цилиндра
Представьте себе ситуацию, когда вам необходимо вычислить объем цилиндра. Вы знаете радиус основания цилиндра равен 5 см, а его высота равна 10 см. Чтобы решить эту задачу, вам нужно использовать корни.
Объем цилиндра можно выразить следующей формулой:
V = π * r² * h
Где r - радиус, h - высота.
Подставив значения, получим:
V = π * 5² * 10
Для нахождения значения V, мы можем воспользоваться операцией извлечения корня:
V = π * 25 * 10 = 250π ≈ 785.4
Таким образом, объем цилиндра составляет примерно 785.4 кубических сантиметров.
Это лишь несколько примеров задач, в которых использование корней является необходимым. В реальной жизни корни могут применяться в различных областях, таких как строительство, физика, экономика и др. Понимание этой математической операции позволяет нам получать точные и достоверные результаты в решении разнообразных задач.
Как найти корни выражения с помощью графиков
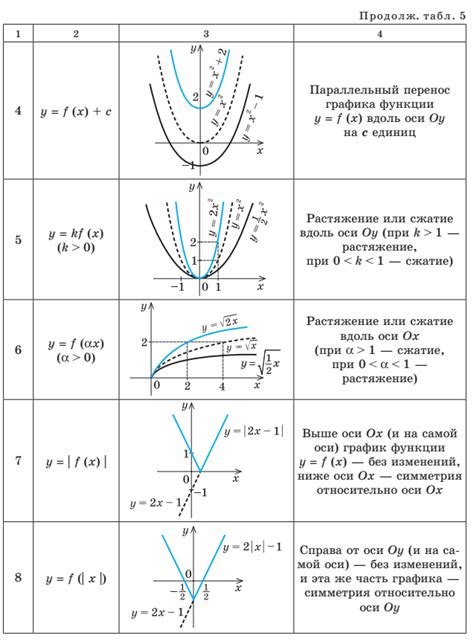
Для начала нужно построить график выражения с помощью графической программы или онлайн-ресурса. Затем проведите горизонтальную линию на уровне оси абсцисс (горизонтальной оси). Затем определите точки пересечения графика с этой линией. Эти точки будут значениями корней выражения.
Ограничьтесь рассмотрением только тех точек на графике, где выражение пересекает ось абсцисс. Исключите ситуации, когда функция только касается горизонтальной линии.
Если у вас есть несколько выражений, вы также можете построить графики этих выражений на одном графике и определить точки их пересечения. Все точки пересечения будут значениями корней всех выражений.
Значения корней, найденные с помощью графиков, являются приближенными из-за ограничений точности рисования графика. Для получения более точных значений рекомендуется использовать аналитические методы, такие как факторизация или использование формул.