Алгебра является одним из основных разделов математики, который изучается в школах на протяжении нескольких лет. Одним из важных навыков, которые нужно овладеть, является поиск значения выражения. В этой статье мы рассмотрим, как найти значение выражения в алгебре 7 класса с помощью степеней и предоставим вам полезные советы и примеры.
Степени являются основным инструментом для работы с выражениями в алгебре. Они позволяют упростить сложные математические операции и найти значения выражений. В основе степеней лежит понятие возведения числа в степень. Например, число 2 в степени 3 можно записать как 2^3, что равно 2 * 2 * 2 = 8.
Чтобы найти значение выражения с использованием степеней, необходимо следовать нескольким простым шагам. Во-первых, необходимо вычислить каждую степень. Затем необходимо выполнить операции с полученными результатами, например, сложение, вычитание, умножение или деление. Наконец, найденное значение будет являться ответом на исходное выражение.
Подход к решению алгебраических выражений
Для нахождения значения алгебраического выражения, вам необходимо внимательно изучить выражение и заменить в нем все переменные на известные значения. Затем вычислите каждую часть выражения поочередно, используя правила арифметики.
Например, если дано выражение 2x + 3y и значения x = 4 и y = 2, заменим переменные в выражении и вычислим:
- Подставим x = 4: 2 * 4 + 3y
- Выполним умножение: 8 + 3y
- Подставим y = 2: 8 + 3 * 2
- Выполним умножение: 8 + 6
- Выполним сложение: 14
Полученное значение 14 – это значение данного алгебраического выражения при данных значениях переменных.
Следуя приведенным примерам и используя правила арифметики, вы сможете решить алгебраические выражения и получить их значения с помощью степеней.
Примеры использования степеней в алгебре 7 класса
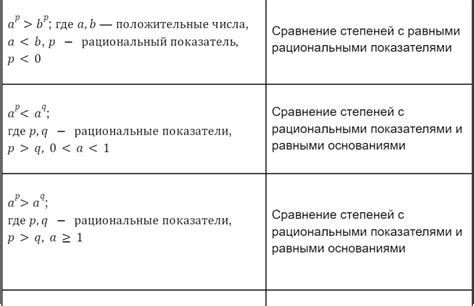
- Вычисление степени числа: например, вычислить значение выражения 3^4 (3 в четвертой степени). Для этого нужно умножить число 3 на само себя 4 раза: 3 * 3 * 3 * 3 = 81. Таким образом, 3^4 равно 81.
- Возведение в степень с отрицательным показателем: например, вычислить 2^-3. В этом случае нужно взять обратное значение числа (1/2) и возвести его в положительную степень 3: (1/2) * (1/2) * (1/2) = 1/8. Таким образом, 2^-3 равно 1/8.
- Вычисление значения выражений с несколькими степенями: например, вычислить значение выражения (2^3)^2. Сначала возводим число 2 в третью степень: 2^3 = 8. Затем возводим полученный результат во вторую степень: 8^2 = 64. Таким образом, (2^3)^2 равно 64.
- Упрощение выражений с отрицательными степенями: например, упростить выражение 3^2 / 3^-1. Сначала нужно упростить отрицательную степень: 3^-1 = 1/3. Затем делим числа с одинаковым основанием: 3^2 / 1/3 = (3^2) * (3/1) = 9 * 3 = 27. Таким образом, 3^2 / 3^-1 равно 27.
Это лишь несколько примеров использования степеней в алгебре 7 класса. С помощью степеней можно решать различные задачи и упрощать выражения, что значительно облегчает работу с алгеброй.