Квадратные уравнения - это одни из самых основных, но при этом и наиболее сложных задач в алгебре. Они часто возникают в различных областях науки и техники, и поэтому важно знать, как найти их значения.
Квадратные уравнения имеют следующий вид: ax^2 + bx + c = 0, где a, b и c - известные коэффициенты, а x - неизвестное значение, которое требуется найти. В алгебре существует специальная формула, позволяющая найти значение x.
Шаги для нахождения значения x в квадратном уравнении:
- Шаг 1: Раскрыть скобки и привести уравнение к виду ax^2 + bx + c = 0.
- Шаг 2: Определить значения коэффициентов a, b и c.
- Шаг 3: Вычислить дискриминант по формуле D = b^2 - 4ac. Дискриминант является ключевым показателем для определения количества и типа корней уравнения.
- Шаг 4: Определить количество и тип корней квадратного уравнения на основе значения дискриминанта.
- Шаг 5: Если дискриминант положительный (D > 0), то у уравнения два различных корня x1 и x2.
- Шаг 6: Если дискриминант равен нулю (D = 0), то у уравнения есть один корень, который является действительным и равным x.
- Шаг 7: Если дискриминант отрицательный (D
Важно помнить, что найти значения x в квадратном уравнении может быть сложной задачей. Поэтому необходимо тщательно выполнять все шаги и не допускать ошибок в расчетах. Если возникают сложности, всегда можно обратиться к учителю или использовать специализированные алгебраические программы и калькуляторы.
Что такое квадратное уравнение
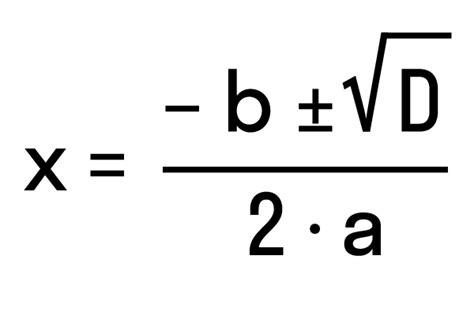
Они называются квадратными уравнениями, потому что выражение ax2 включает квадрат переменной x. Квадратные уравнения встречаются в различных областях математики и физики, и они имеют важное практическое применение.
Главная цель в решении квадратных уравнений состоит в нахождении всех значений переменной x, которые удовлетворяют данному уравнению.
Один из самых распространенных методов решения квадратных уравнений - это использование формулы дискриминанта.
Формула дискриминанта выглядит следующим образом:
D = b2 - 4ac
Если значение дискриминанта D больше нуля, то квадратное уравнение имеет два различных решения:
x1 = (-b + √D) / (2a)
x2 = (-b - √D) / (2a)
Если значение дискриминанта D равно нулю, то квадратное уравнение имеет одно решение:
x = -b / (2a)
Если значение дискриминанта D меньше нуля, то квадратное уравнение не имеет действительных корней.
Понимание и умение решать квадратные уравнения часто требуется при решении задач в финансовой математике, физике, инженерии и других областях. Это важное математическое умение, которое помогает анализировать и решать различные задачи и проблемы.
Зачем искать значение x в квадратном уравнении
Поиск значения x в квадратном уравнении является неотъемлемой частью решения многих задач. Например, этот процесс позволяет найти корни уравнения, что в свою очередь может помочь в решении геометрических проблем, нахождении точек пересечения графиков функций, определении времени достижения определенных условий в физических моделях и т.д.
Значение x в квадратном уравнении может также использоваться для определения экстремальных точек на графике функции. Нахождение таких точек может быть полезно при оптимизации процесса или исследовании поведения системы.
Таким образом, поиск значения x в квадратном уравнении является не только математическим упражнением, но и важным инструментом для решения различных задач и развития аналитических навыков.
Шаг 1: Определение коэффициентов уравнения
Перед тем как начать решать квадратное уравнение, необходимо определить его коэффициенты. Квадратное уравнение имеет вид:
ax2 + bx + c = 0,
где a, b и c - это числовые значения, называемые коэффициентами.
В этом уравнении:
- a - коэффициент при переменной x2.
- b - коэффициент при переменной x.
- c - свободный член, т.е. коэффициент при переменной, которая не содержит x.
Как найти коэффициенты в квадратном уравнении
Для того чтобы найти коэффициенты в квадратном уравнении, необходимо привести его к каноническому виду или использовать методы выделения полного квадрата. Коэффициент a можно найти, опираясь на первый член уравнения, коэффициент b - на второй член, а коэффициент c - на свободный член.
Если уравнение уже находится в каноническом виде, то коэффициенты очевидны из уравнения. Если уравнение не в каноническом виде, то необходимо выполнить несколько шагов для его приведения.
1. Проверяем, что коэффициент при старшем члене a не равен нулю. Если коэффициент a равен нулю, то уравнение уже не является квадратным.
2. Если коэффициент a не равен нулю, то выполняем действия для приведения уравнения.
3. Выполняем операции для получения канонического вида уравнения.
4. Коэффициенты a, b и c определяются путем сравнения каждого члена уравнения с соответствующим членом в каноническом виде уравнения.
Таким образом, нахождение коэффициентов в квадратном уравнении зависит от приведения уравнения к каноническому виду или использования метода выделения полного квадрата.
Пример определения коэффициентов уравнения
Рассмотрим пример пошагового определения коэффициентов в квадратном уравнении.
Дано квадратное уравнение: ax2 + bx + c = 0.
Чтобы определить значения коэффициентов a, b и c, необходимо рассмотреть уравнение и выделить соответствующие части.
Коэффициент a является коэффициентом при x2, b - при x и c - свободным членом.
Например, для уравнения 2x2 + 5x - 3 = 0:
a = 2, так как коэффициент при x2 равен 2.
b = 5, так как коэффициент при x равен 5.
c = -3, так как -3 является свободным членом.
Теперь, имея значения коэффициентов, можно приступить к решению уравнения и определению значений переменной x.
Шаг 2: Расчет дискриминанта
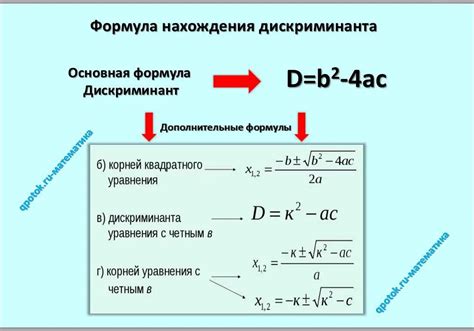
Дискриминант вычисляется по формуле: D = b^2 - 4ac, где a, b и c - коэффициенты квадратного уравнения ax^2 + bx + c = 0.
Если дискриминант больше нуля (D > 0), то у уравнения два различных действительных корня.
Если дискриминант равен нулю (D = 0), то у уравнения один действительный корень, который является двукратным.
Если дискриминант меньше нуля (D
Рассчитаем дискриминант для нашего уравнения. Подставим значения коэффициентов a, b и c в формулу и произведем необходимые вычисления.
Что такое дискриминант и как его рассчитать
| D = | b2 - 4ac |
где a, b и c - коэффициенты квадратного уравнения вида ax2 + bx + c = 0.
Расчет дискриминанта помогает понять, какие решения может иметь уравнение:
- Если D > 0, то уравнение имеет два различных корня.
- Если D = 0, то уравнение имеет один корень, который называется кратным.
- Если D
Дискриминант является полезным инструментом при решении квадратных уравнений, так как он позволяет понять их природу и предсказать число и тип решений.