Треугольник – одна из самых известных и изучаемых геометрических фигур. Знание его сторон и углов необходимо во многих областях, начиная от строительства и заканчивая физикой. Одна из наиболее интересных задач – найти стороны треугольника по данному катету и высоте. Это очень полезное умение, которое позволяет сэкономить время и раскрыть тайны геометрии.

Для решения задачи необходимо знать основные формулы геометрии. Если дан катет и высота, то можно использовать теорему Пифагора для нахождения гипотенузы. Также можно использовать формулу для нахождения площади треугольника, которая равна половине произведения длины катета и высоты.

Важно помнить, что сторона треугольника не может быть отрицательной или равной нулю. Поэтому при решении задачи нужно проверить корректность полученных значений и исключить возможность ошибки.

Определение сторон треугольника по катету и высоте

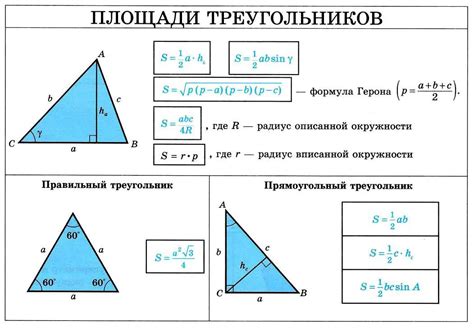
Теорема Пифагора позволяет находить стороны треугольника, если известны длины катета и высоты. Согласно этой теореме, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Предположим, что у нас есть треугольник, в котором один катет известен, а также известна высота, опущенная на этот катет. Обозначим длину известного катета как а, а длину высоты – как h. Мы хотим найти длину гипотенузы треугольника и длину другого катета.

По теореме Пифагора мы знаем, что сумма квадратов катетов равна квадрату гипотенузы. Поэтому, если возведем известный катет в квадрат и от этого числа отнимем квадрат высоты, получим результат, который можно извлечь квадратным корнем. Так мы найдем длину гипотенузы.

А чтобы найти длину другого катета, мы можем использовать теорему Пифагора снова. Если из квадрата гипотенузы вычесть квадрат известного катета и извлечь квадратный корень из этого числа, мы получим длину второго катета.

Что такое стороны треугольника?

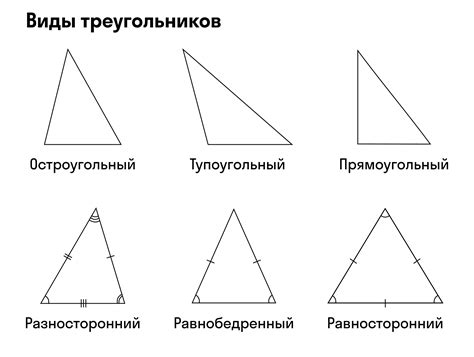
Стороны треугольника играют важную роль в геометрии, так как они определяют его форму и свойства. Например, по длинам сторон можно определить тип треугольника: равносторонний, равнобедренный или разносторонний. Кроме того, знание длин сторон позволяет решать задачи с использованием теоремы Пифагора, находить площадь треугольника и выполнять другие геометрические вычисления.

Запомните: треугольник всегда имеет три стороны, и каждая из них играет свою важную роль в геометрии и решении задач.

Расчет сторон треугольника по катету и высоте

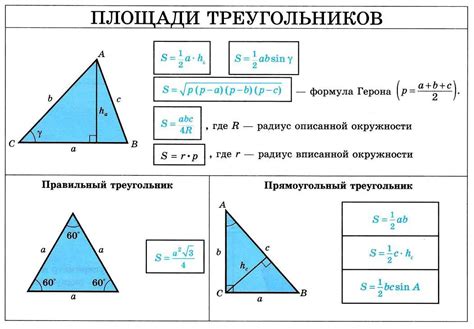
Для расчета сторон треугольника по известному катету и высоте можно использовать теорему Пифагора.

Теорема Пифагора утверждает, что для прямоугольного треугольника с катетами a и b и гипотенузой c выполняется следующее соотношение:

a^2 + b^2 = c^2

Если известен один катет (назовем его a) и высота (назовем ее h), то можно найти второй катет (b) и гипотенузу (c).

Для этого применим теорему Пифагора:

a^2 + h^2 = c^2

Из этого уравнения можно найти значения для b и c:

b = √(c^2 - a^2)

c = √(a^2 + h^2)

Таким образом, если известны значения одного катета и высоты, можно рассчитать значения второго катета и гипотенузы треугольника.