На все времена графики функций являлись стандартным способом визуализации математических зависимостей. Сегодня мы поговорим о графике для функции y=x^2, которая представляет собой квадратичную функцию. Построение графика такой функции является важным уроком для учеников 7 класса алгебры.
Перед началом построения графика необходимо понять, что для каждого значения x, функция y=x^2 будет выдавать соответствующее значение y. Например, если x=2, то y=2^2=4. Таким образом, мы можем создать таблицу со значениями x и y, чтобы получить координаты точек для графика.
Когда таблица значений готова, мы можем начать рисовать график. Для этого нам понадобится ось x (горизонтальная ось) и ось y (вертикальная ось). Начертите эти оси на листе бумаги, оставив достаточно места для рисования графика.
График функции y=x^2 для 7 класса алгебры
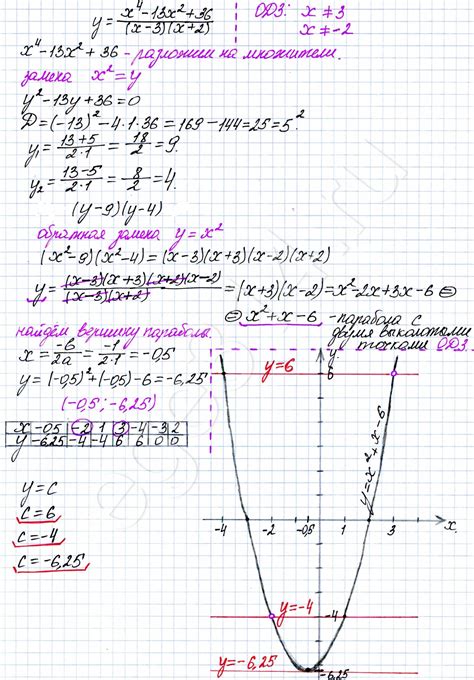
Для построения графика функции y=x^2 достаточно знать несколько пар значений x и соответствующих им значений y. Например, если взять x=-2, -1, 0, 1 и 2, то получим следующие значения:
| x | y=x^2 |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
Подставляя эти значения в уравнение y=x^2, можно построить график функции. Для каждого значения x отмечаем на координатной плоскости точку с координатами (x, y), где y равно значению функции для данного x. Затем соединяем эти точки плавной кривой линией, и получаем график функции y=x^2.
График функции y=x^2 является симметричным относительно оси y и всегда положительным. Он увеличивается с увеличением значений x, что означает, что при увеличении значения x, значение y также увеличивается, но нелинейно.
Построение графиков функций - важный этап изучения алгебры. График функции y=x^2 помогает ученикам визуализировать свойства и поведение данной функции, а также позволяет решать различные задачи, связанные с этой функцией.
Что такое функция y=x^2?
Таким образом, функция y=x^2 описывает параболу с вершиной в начале координат (0, 0) и осью симметрии, параллельной оси y. Значения функции y=x^2 увеличиваются с ростом значения переменной x.
Для визуализации функции y=x^2 мы можем построить график на плоскости с осями x и y. На графике будут отмечены некоторые значимые точки, а также будет видна общая форма параболы.
Чтобы построить график функции y=x^2, мы можем выбрать несколько значений переменной x, вычислить соответствующие значения переменной y и отметить эти точки на графике. Затем мы соединим все точки, получив плавную кривую, которая будет представлять функцию y=x^2.
Таблица значений функции y=x^2 может выглядеть следующим образом:
| x | y |
|---|---|
| -3 | 9 |
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
Используя эти значения, мы можем построить график функции y=x^2 и увидеть, как значения y меняются в зависимости от значения x.
Как построить координатную плоскость?
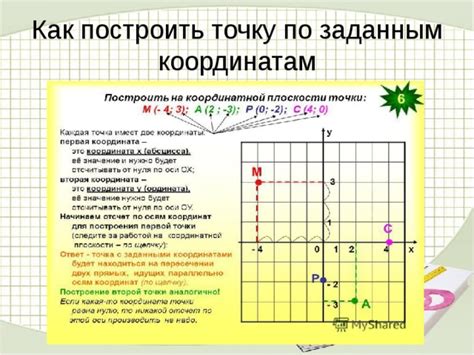
- Отметьте начало координат. Начало координат обозначается точкой (0, 0) и находится посередине плоскости.
- Отметьте оси координат. На координатной плоскости есть две оси - горизонтальная ось, называемая осью X, и вертикальная ось, называемая осью Y. Ось X обычно располагается горизонтально и проходит через начало координат, а ось Y располагается вертикально и также проходит через начало координат.
- Подпишите оси координат. На оси X обычно подписывают значения справа от начала координат, а на оси Y - значением сверху от начала координат. Нумерация на осях зависит от вашей задачи.
- Разделите оси на равные отрезки. Разделите оси X и Y на равные отрезки с помощью рулетки или линейки. Эти отрезки будут использоваться для значений по осям.
- Отметьте точки данных. Если у вас есть конкретные значения, которые нужно отобразить на плоскости, отметьте эти точки на их соответствующих координатах. Например, для функции y = x^2, вы можете отметить точки (1, 1), (2, 4), (3, 9) и так далее.
- Соедините точки для построения графика. Чтобы построить график функции, соедините отмеченные точки прямыми линиями.
Теперь у вас есть готовая координатная плоскость, на которой вы можете построить график функции y = x^2 или любой другой график, используя значения координатных точек.
Как построить график функции y=x^2?
Для начала, необходимо понять, что функция y=x^2 является параболой с вершиной в точке (0, 0) и осью симметрии, которая проходит через эту точку. Когда x=0, y также равно 0.
Чтобы построить график функции, вам понадобится система координат. Задайте оси x и y на графической бумаге или используйте программу для построения графиков, если вы работаете с электронным устройством.
Затем, построьте точки, соответствующие значениям функции при разных значениях x. Для этого, возьмите несколько значений x, например -2, -1, 0, 1 и 2, и вычислите соответствующие значения y, используя уравнение y=x^2. Таким образом, вы получите следующие пары значений: (-2, 4), (-1, 1), (0, 0), (1, 1) и (2, 4).
Соедините полученные точки линией, чтобы получить параболу. Заметьте, что ось симметрии параболы проходит через вершину (0, 0). Парабола будет открыта вверх, так как коэффициент при x^2 положительный.
Например, чтобы представить это на графической бумаге, пометьте точку (0, 0) и проведите линию через эту точку. Затем отложите точку (-2, 4) над линией на расстоянии 4 единицы от начала координат и проведите линию, соединяющую ее с точкой (0, 0). Повторите эту процедуру для остальных точек, и вы получите график функции y=x^2.
Теперь, когда вы знаете, как построить график функции y=x^2, практикуйтесь, проводя разные значения x и y для большего понимания этой функции и алгебры в целом.
Анализ графика функции y=x^2
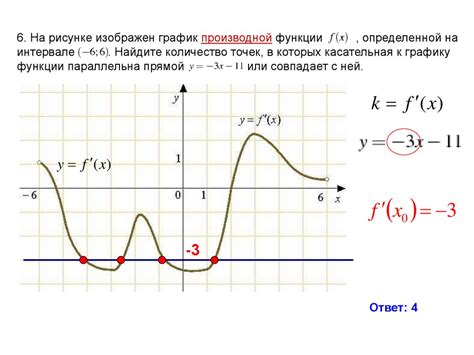
График функции y=x^2 симметричен относительно оси ординат. Значит, если точка p(x,y) лежит на графике функции, то точка -p(-x,y) тоже лежит на нем.
Поскольку функция является параболой, она растет неограниченно как x стремится к плюс бесконечности и минус бесконечности. У ее графика нет максимальных и минимальных значений.
Из формулы функции y=x^2 можно составить таблицу значений, где первый столбец - это значения x, второй столбец - это соответствующие значения y. Например, для x от -3 до 3:
- При x=-3, y=(-3)^2=9
- При x=-2, y=(-2)^2=4
- При x=-1, y=(-1)^2=1
- При x=0, y=(0)^2=0
- При x=1, y=(1)^2=1
- При x=2, y=(2)^2=4
- При x=3, y=(3)^2=9
Из этой таблицы можно построить график функции y=x^2, отметив на координатной плоскости соответствующие точки для каждого значения x.
Практические задания на построение графика
1. Постройте график функции y = 2x. Для этого выберите несколько значений для x, подставьте их в уравнение и найдите соответствующие значения y. Затем отметьте полученные точки на координатной плоскости и проведите прямую через них.
2. Постройте график функции y = -3x + 5. Процедура аналогична предыдущему заданию. Значения x выберите самостоятельно.
3. Постройте график функции y = x2 и определите его особенности. Для этого найдите значения y для нескольких значений x и отразите их на координатной плоскости.
4. Постройте график функции y = -x2 + 4. Аналогично предыдущему заданию, определите особенности графика.
5. Постройте график функции y = |x|. Обратите внимание на поведение функции при отрицательных и положительных значениях x.
6. Постройте график функции y = sqrt(x). Определите, для каких значений x функция определена.
7. Постройте график функции y = 1/x. Обратите внимание на поведение функции вблизи точки x = 0.
8. Постройте график функции y = sin(x). Определите, какие значения y принимает функция и где достигает своих экстремумов.
9. Постройте график функции y = cos(x). Аналогично предыдущему заданию, определите значения y и экстремумы функции.
10. Постройте график функции y = tan(x). Заметьте, что функция тангенс не определена при некоторых значениях x.
Постепенно сложность заданий будет увеличиваться, и вы сможете всё лучше и лучше разбираться с построением графиков различных функций.