Построение точки по заданным координатам - это одна из основных тем, которую изучают учащиеся 6 класса на уроках математики. Это важный навык, который помогает развить понимание графиков и координатной плоскости, а также применять их в решении задач. В данной статье мы рассмотрим основные шаги, необходимые для построения точки на координатной плоскости.
Первым шагом является определение координат точки. Для этого необходимо учитывать две оси: горизонтальную (ось абсцисс) и вертикальную (ось ординат). Горизонтальная ось обозначается буквой x, а вертикальная - буквой y. Координаты точки обычно записываются в формате (x, y).
Вторым шагом является маркировка осей координатной плоскости. Для этого используют линейку и карандаш. Ось абсцисс горизонтальна и простирается слева направо, а ось ординат вертикальна и простирается сверху вниз. Центр плоскости, где пересекаются оси, обозначается буквой O. Важно правильно разметить и промаркировать деления на осях.
Понятие координатной плоскости
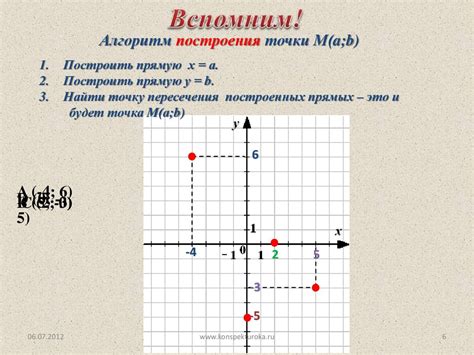
Горизонтальная ось Ox также называется осью абсцисс, а вертикальная ось Oy - осью ординат. Точка пересечения осей называется началом координат и обозначается буквой O. Координаты точек на плоскости задаются парами чисел (x, y), где x - это значение по оси абсцисс, а y - значение по оси ординат.
Чтобы построить точку по ее координатам на координатной плоскости, мы откладываем значение x вдоль оси абсцисс и значение y вдоль оси ординат. Точка, обозначаемая парами чисел (x, y), будет находиться на их пересечении.
Размещение точки на координатной плоскости
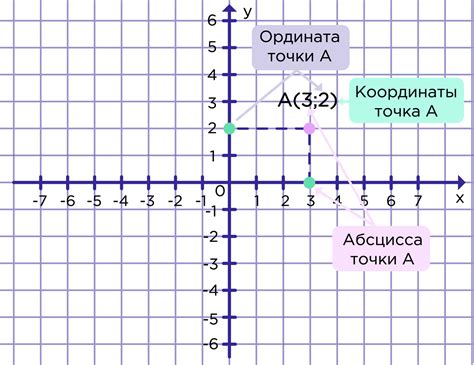
Например, если точка расположена на расстоянии 3 единицы от начала координат по горизонтальной оси вправо (положительная абсцисса), и на 2 единицы вверх по вертикальной оси, то ее координаты будут (3, 2).
При размещении точек на координатной плоскости необходимо помнить, что направление осей может изменяться. Например, вертикальная ось может быть направлена вверх (положительная ордината) или вниз (отрицательная ордината), а горизонтальная ось может быть направлена вправо (положительная абсцисса) или влево (отрицательная абсцисса).
Размещение точек на координатной плоскости позволяет проводить различные геометрические операции, например, находить расстояние между точками или строить графики функций. Важно уметь правильно определять координаты точки и использовать их для решения задач в математике и других науках.
Правила определения координат точки
Абсцисса (x) - это первое число координаты точки и указывает расстояние от точки до вертикальной оси, называемой осью абсцисс.
Ордината (y) - это второе число координаты точки и указывает расстояние от точки до горизонтальной оси, называемой осью ординат.
Для определения координат точки нужно:
| Шаг 1: | Найти пересечение осей абсцисс и ординат - начало координат. |
| Шаг 2: | Из начала координат провести вертикальный отрезок, который будет указывать значение абсциссы (x) точки. |
| Шаг 3: | Из точки, где пересекается вертикальный отрезок с горизонтальной осью (ось ординат), провести горизонтальный отрезок. Этот отрезок будет указывать значение ординаты (y) точки. |
| Шаг 4: | Записать значение абсциссы (x) и ординаты (y) в порядке (x, y). |
Таким образом, зная абсциссу и ординату точки, можно легко определить ее координаты на координатной плоскости.
Построение точки с положительными координатами
1. Взять большой лист бумаги и нарисовать на нем декартову плоскость. Декартова плоскость представляет собой систему координат с осью X (горизонтальная) и осью Y (вертикальная).
2. Определить значения координат точки. Например, пусть точка имеет координаты (3, 4).
3. На оси X отложить 3 единицы вправо от начала координат. На оси Y отложить 4 единицы вверх от начала координат. Таким образом, мы получим позицию точки (3, 4).
4. Используя линейку, провести от начала координат до точки прямые линии по осям X и Y. Таким образом, мы получим построение точки с положительными координатами (3, 4).
Построение точки с положительными координатами помогает понять принцип работы системы координат и развивает навыки пространственного мышления. Этот навык будет полезен не только в учебе, но и в повседневной жизни при работе с картами, планами и другими графическими представлениями данных.
Построение точки с отрицательными координатами
При построении точек на координатной плоскости в 6 классе математики, мы сталкиваемся с различными координатами, включая отрицательные числа. Отрицательные числа на координатной плоскости находятся слева от нуля на оси абсцисс и ниже нуля на оси ординат.
Чтобы построить точку с отрицательными координатами, мы сначала определяем значение абсциссы и ординаты указанной точки. Затем мы перемещаемся влево от начала координат по оси абсцисс на нужное количество единиц в соответствии с указанной абсциссой. После этого перемещаемся вниз от начала координат по оси ординат на нужное количество единиц в соответствии с указанной ординатой. В месте пересечения двух осей находим построенную точку.
Построение точки с нулевыми координатами
Такая точка называется началом координат или точкой O.
Она обозначается символом O, который располагается в центре координатной сетки.
Важно понимать, что координаты начала координат равны нулю: (0,0).
Построение начала координат не требует вычислительных действий, так как оно является общедоступным и известным всем.
Знание начала координат поможет в дальнейшем в изучении различных геометрических фигур и выполнении операций с векторами.
Примеры построения точек по заданным координатам
В математике точка обычно обозначается парой чисел, которые называются координатами. Построение точки на плоскости происходит следующим образом:
1. Определите систему координат. Обычно используются декартовые координаты, которые состоят из двух перпендикулярных осей - горизонтальной (ось абсцисс) и вертикальной (ось ординат).
2. Определите координаты точки. Например, точка А имеет координаты (2, 3), что означает, что она находится на 2 единицы правее начала координат (нулевое значение по оси абсцисс) и 3 единицы выше начала координат (нулевое значение по оси ординат).
3. Постройте отметку на соответствующих осях, чтобы обозначить координаты точки. Для точки А с координатами (2, 3) на оси абсцисс будет отметка 2 и на оси ординат - отметка 3.
4. Соедините отметки на осях, чтобы получить точку. В случае с точкой А с координатами (2, 3) соедините отметку 2 на оси абсцисс с отметкой 3 на оси ординат.
Например, если вам задана точка А с координатами (2, 3), то построение этой точки будет выглядеть следующим образом:
Шаг 1:
Определение системы координат:
Выберем декартову систему координат.
Ось абсцисс будет горизонтальной, а ось ординат - вертикальной.
Шаг 2:
Определение координат точки:
Точка А имеет координаты (2, 3).
Она находится на 2 единицы правее начала координат и 3 единицы выше начала координат.
Шаг 3:
Построение отметок на осях:
Для точки А с координатами (2, 3) на оси абсцисс будет отметка 2, а на оси ординат - отметка 3.
Шаг 4:
Построение точки:
Соединяем отметку 2 на оси абсцисс с отметкой 3 на оси ординат.
Таким образом, точка А с координатами (2, 3) будет находиться на плоскости на пересечении отметок 2 и 3 на соответствующих осях.
Подведение итогов и закрепление материала

- Мы изучили, как построить точку на координатной плоскости по заданным координатам.
- Мы познакомились с основными понятиями: абсцисса (первая координата) и ордината (вторая координата).
- Мы поняли, что точка на плоскости определяется своими координатами.
- Мы узнали, что координаты точки могут быть положительными и отрицательными числами.
- Мы научились строить точку на координатной плоскости в соответствии с ее координатами.
- Мы выяснили, что в случае, когда у нас есть только одна координата, точка строится на соответствующей оси.
- Мы разобрали примеры задач, в которых необходимо было построить точки по заданным координатам.
Теперь мы полностью понимаем, как построить точку на координатной плоскости по заданным координатам. Это навык, который поможет нам в дальнейшем изучении математики.