В современном мире, где точность и математика играют важнейшую роль, умение определить число до целых является необходимым навыком. Этот полезный навык может быть полезен при решении различных задач, а также в повседневной жизни. Если вы хотите узнать, как определить число до целых, вам пригодятся некоторые советы и примеры, которые мы рассмотрим в этой статье.
Во-первых, одним из основных способов определения числа до целых является округление. Округление позволяет привести число к ближайшему целому значению. Существуют разные правила округления, чтобы выбрать наиболее подходящий вариант в каждой конкретной ситуации. Например, существует правило "больше или меньше пяти", которое гласит, что если десятичная часть числа меньше пяти, то число округляется в меньшую сторону, а если она больше или равна пяти, то - в большую сторону.
Во-вторых, помимо округления, существуют и другие методы определения числа до целых. К примеру, метод "Отсечения" позволяет просто отбросить десятичную часть и оставить только целую. Это может быть полезно в тех случаях, когда нам не требуется точность и достаточно знать только целое значение числа. Как правило, отсечение применяется в простых математических операциях, таких как сложение, вычитание, умножение или деление.
Итак, теперь вы знакомы с некоторыми основными способами определения числа до целых. Округление и отсечение являются основными методами, которые позволяют получить приближенное целое значение числа. Однако, стоит помнить, что в каждой конкретной ситуации может потребоваться применение своего метода, чтобы достичь желаемой точности. Теперь, когда вы освоили эти навыки, вы можете применить их в практических задачах и повседневной жизни.
Основные понятия и методы
Определение числа до целых может быть полезно во многих ситуациях, например, для округления чисел, расчетов с десятичными дробями или для установления границ числовых интервалов.
Округление - один из способов определения числа до целых. При округлении число близкое к целому округляется до ближайшего целого числа.
Методы округления:
Округление вниз - число округляется до ближайшего целого числа, меньшего или равного исходному числу. Например, число 2.8 округляется до 2.
Округление вверх - число округляется до ближайшего целого числа, большего или равного исходному числу. Например, число 2.2 округляется до 3.
Округление к ближайшему целому числу - число округляется до ближайшего целого числа. Если число находится на равном удалении от двух целых чисел, то оно округляется к четному целому числу. Например, число 2.5 округляется до 2, а число 3.5 округляется до 4.
Округление с заданной точностью - число округляется до заданного количества знаков после запятой. Например, число 2.345 округленное до двух знаков после запятой будет равно 2.35.
Целая часть числа - это наибольшее целое число, которое меньше или равно исходному числу.
Дробная часть числа - это часть числа между целой частью и следующим целым числом.
Знание основных понятий и методов определения числа до целых позволит вам легче работать с десятичными числами и использовать их в различных математических операциях и расчетах.
Как округлить число в меньшую сторону
Для округления числа в меньшую сторону можно воспользоваться функцией floor() в языке программирования, таких как C++, Python, JavaScript. Она возвращает наибольшее целое число, которое не превышает заданное число.
Вот пример кода на языке Python, демонстрирующий округление числа в меньшую сторону:
import math x = 4.9 rounded_x = math.floor(x)
В данном примере число 4.9 округляется в меньшую сторону до целого числа 4.
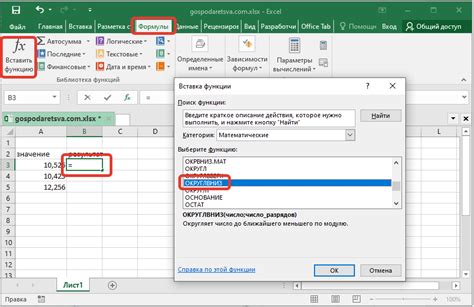
Если вам необходимо округлить число в меньшую сторону в Excel, вы можете использовать функцию FLOOR(). Например, следующая формула округляет число A1 в меньшую сторону:
=FLOOR(A1, 1)
Это был краткий обзор того, как округлить число в меньшую сторону. Учитывайте, что правила округления различаются в зависимости от языка программирования или программы, поэтому всегда обратитесь к документации или официальному руководству, чтобы узнать точные правила в вашем случае.
Как округлить число в большую сторону
Округление чисел может быть полезным при работе с математическими вычислениями. Иногда требуется округлять число в большую сторону, чтобы получить более точный результат.
Для округления числа в большую сторону можно использовать функцию Math.ceil() в JavaScript. Эта функция возвращает наименьшее целое число, большее или равное указанному числу.
Пример использования:
| Исходное число | Округленное число |
|---|---|
| 4.2 | 5 |
| 3.7 | 4 |
| 5.9 | 6 |
Таким образом, при округлении числа 4.2 в большую сторону получим число 5, 3.7 округлится до 4, а число 5.9 будет округлено до 6.
Утилиты округления чисел также доступны в других языках программирования, например, в Python есть функция math.ceil().
Использование правильного метода округления помогает получить результаты более точными и приближенными к ожидаемым значениям.
Как округлить число до ближайшего целого
Метод Math.round()
- Метод Math.round() округляет число до ближайшего целого значения.
- Если число имеет десятичную часть от 0.5 или больше, то число будет округлено в большую сторону.
- Если число имеет десятичную часть меньше 0.5, то число будет округлено в меньшую сторону.
- Метод возвращает значение типа number.
Пример:
let number = 4.6;
let roundedNumber = Math.round(number);
console.log(roundedNumber); // Output: 5
Метод Math.ceil()
- Метод Math.ceil() округляет число вверх до ближайшего целого значения.
- Вне зависимости от значения десятичной части, число всегда будет округлено в большую сторону.
- Метод возвращает значение типа number.
Пример:
let number = 4.6;
let roundedNumber = Math.ceil(number);
console.log(roundedNumber); // Output: 5
Метод Math.floor()
- Метод Math.floor() округляет число вниз до ближайшего целого значения.
- Вне зависимости от значения десятичной части, число всегда будет округлено в меньшую сторону.
- Метод возвращает значение типа number.
Пример:
let number = 4.6;
let roundedNumber = Math.floor(number);
console.log(roundedNumber); // Output: 4
Вы можете выбрать подходящий метод округления в зависимости от ваших нужд. Используйте эти методы, когда вам нужно округлить число до ближайшего целого значения в вашем JavaScript коде.
Как округлить число до определенного знака после запятой

Иногда требуется округлить число до определенного знака после запятой, чтобы результат был более точным или соответствовал определенным требованиям. В этом разделе мы рассмотрим несколько способов округления числа до определенного количества знаков после запятой.
1. Использование функции toFixed()
JavaScript предоставляет функцию toFixed(), которая позволяет округлить число до заданного количества знаков после запятой. Например, чтобы округлить число 5.6789 до двух знаков после запятой, мы можем использовать следующий код:
let number = 5.6789;
let roundedNumber = number.toFixed(2);
В результате переменная roundedNumber будет содержать округленное значение 5.68.
2. Использование функции Math.round()
Еще один способ округления числа до определенного количества знаков после запятой - использовать функцию Math.round(). Например, чтобы округлить число 5.6789 до двух знаков после запятой, мы можем использовать следующий код:
let number = 5.6789;
let roundedNumber = Math.round(number * 100) / 100;
В результате переменная roundedNumber будет содержать округленное значение 5.68.
3. Использование функции Number.prototype.toFixed()
Третий способ округления числа до определенного количества знаков после запятой - использовать метод toFixed() встроенного объекта Number. Например, чтобы округлить число 5.6789 до двух знаков после запятой, мы можем использовать следующий код:
let number = 5.6789;
let roundedNumber = Number(number.toFixed(2));
В результате переменная roundedNumber будет содержать округленное значение 5.68.
Используйте один из этих способов в зависимости от ваших требований и предпочтений. У каждого из них есть свои особенности, поэтому важно выбрать наиболее подходящий для конкретной задачи.
Как определить число до целых с помощью математических функций

Для определения числа до целых можно использовать следующие математические функции:
- Функция floor(x) возвращает наибольшее целое число, которое меньше или равно заданному числу x. Например, floor(4.9) вернет 4, а floor(-2.5) вернет -3.
- Функция ceil(x) возвращает наименьшее целое число, которое больше или равно заданному числу x. Например, ceil(4.1) вернет 5, а ceil(-2.8) вернет -2.
- Функция trunc(x) отбрасывает дробную часть числа и возвращает только целую часть. Например, trunc(3.7) вернет 3, а trunc(-1.5) вернет -1.
Каждая из этих функций имеет свое применение в определении числа до целых. Выбор функции зависит от задачи, которую вы решаете и требований к точности результата.
Например, если вам необходимо получить наибольшее целое число, которое меньше или равно заданному числу, вы можете использовать функцию floor(x). Если же вам нужно округлить число вверх до ближайшего целого числа, используйте функцию ceil(x).
Использование математических функций позволяет точно определить число до целых и избежать ошибок при округлении. Будьте внимательны при выборе функции и применении ее в своем коде!
Примеры использования округления чисел в программировании

В программировании округление чисел может быть полезным во многих ситуациях. Рассмотрим несколько примеров:
Вычисление среднего значения:
int[] numbers = {1, 2, 3, 4, 5}; double average = Math.round(Arrays.stream(numbers).average().orElse(0));В данном примере мы используем метод
Math.round()для округления среднего значения массива чисел до целого.Подсчет налогов:
double income = 50000; double taxRate = 0.25; double tax = Math.round(income * taxRate);Здесь мы применяем округление для подсчета суммы налога на заданный доход с использованием заданной ставки.
Отображение процента выполнения:
int totalTasks = 10; int completedTasks = 7; double progress = Math.round((double) completedTasks / totalTasks * 100);В данном случае мы округляем процент выполнения задач, чтобы отобразить его пользователю в виде целого числа.
Это лишь некоторые примеры использования округления чисел в программировании. В каждом конкретном случае округление может иметь свои особенности и требования, поэтому важно подходить к этому вопросу с учетом контекста и потребностей конкретной задачи.