Высота треугольника - одна из важных характеристик этой геометрической фигуры, которая проводится из вершины треугольника и перпендикулярна к противолежащей стороне. В этой статье мы рассмотрим, как построить высоту треугольника с тупым углом.
Для начала необходимо помнить, что тупым углом называется угол, который больше 90 градусов. Обычно, высоту треугольника легко найти, если известны длины всех его сторон. Однако, в случае с тупым углом, этот процесс может быть несколько сложнее.
Чтобы построить высоту треугольника с тупым углом, достаточно знать следующий алгоритм. Возьмите вершину треугольника, противолежащую тупому углу, и проведите луч через нее, перпендикулярно к противолежащей стороне. Точка пересечения этого луча с противолежащей стороной будет являться конечной точкой высоты треугольника.
Высота треугольника с тупым углом позволит определить его площадь и произвести множество вычислений. Кроме того, знание алгоритма построения высоты позволит вам более глубоко разобраться в строении треугольников и их свойствах.
Шаги для построения высоты треугольника с тупым углом
Шаг 1: Возьмите лист бумаги и нарисуйте на нем треугольник с тупым углом. Чтобы его построить, проведите две стороны треугольника, затем на одной из них отложите отрезок, который будет являться основанием высоты.
Шаг 2: Cоедините конец отрезка, который является основанием высоты, с противоположным углом треугольника. Эта линия будет служить высотой.
Шаг 3: Удостоверьтесь, что высота пересекает противоположную сторону треугольника перпендикулярно. Проведите линию, если это необходимо.
Шаг 4: Визуально проверьте, что ваша линия является высотой треугольника, то есть пересекает тупой угол и противоположную сторону на прямом угле.
Шаг 5: Убедитесь, что все линии точно проведены и не содержат ошибок. Измерьте длину основания высоты и саму высоту, если это необходимо.
Шаг 6: Отметьте на вашем рисунке точку пересечения высоты и основания треугольника. Вы будете использовать эту точку в дальнейшем решении задач, связанных с треугольником с тупым углом.
Следуя этим шагам, вы можете построить высоту треугольника с тупым углом. Инструменты, которые вам могут помочь в этом процессе, включают линейку, карандаш и компас.
Определите треугольник с тупым углом
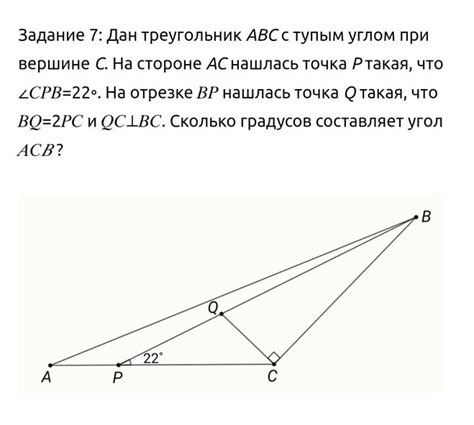
Существуют несколько способов определить, является ли угол тупым:
- Измерьте угол с помощью гониометра или другого инструмента для измерения углов. Если угол больше 90 градусов, то он является тупым.
- Проверьте сумму двух других углов треугольника. Если сумма двух углов меньше 90 градусов, то третий угол является тупым.
- Используйте теорему косинусов. Если одна из сторон треугольника больше суммы квадратов двух других сторон, то треугольник имеет тупой угол напротив этой стороны.
Определение треугольника с тупым углом может быть полезным при построении его высоты, так как тупые углы треугольника помогают определить, где высота пересекает стороны треугольника.
Найдите точку пересечения сторон треугольника

Чтобы найти точку пересечения сторон треугольника, следуйте следующим шагам:
- Проведите прямую, проходящую через одну из сторон треугольника. Вы можете использовать линейку или другие инструменты для рисования прямой.
- Проведите прямую через другую сторону треугольника, так чтобы она пересекалась с первой прямой. Убедитесь, что эта прямая пересекает первую прямую внутри треугольника, а не за его пределами.
- Точка пересечения становится основанием высоты треугольника. Обозначьте ее как точку H.
Теперь вы можете продолжить построение высоты треугольника с тупым углом, используя найденную точку пересечения сторон. Возьмите линейку и проведите прямую линию от точки H до противоположной вершины треугольника. Таким образом, вы построите высоту, которая будет перпендикулярна этой стороне треугольника и проходит через тупой угол.
Не забудьте проверить правильность построения, убедившись, что высота проходит именно через тупой угол треугольника и перпендикулярно противоположной стороне.
Примечание: Если вы не уверены в правильности построения, лучше обратиться к учебнику по геометрии или проконсультироваться с учителем, чтобы получить дополнительные инструкции и помощь.