НОД и НОК - это два важных понятия, которые помогут вам решать задачи на числах. НОД, или наибольший общий делитель, это наибольшее число, которое одновременно делит два или более числа без остатка. НОК, или наименьшее общее кратное, это наименьшее число, которое делится без остатка на два или более числа.
Найдите НОД чисел 24 и 36. Вначале мы можем перечислить все делители данных чисел и найти их общие: для числа 24 это 1, 2, 3, 4, 6, 8, 12, 24, а для числа 36 - 1, 2, 3, 4, 6, 9, 12, 18, 36. Наибольшее общее число из этих перечислений - 12, так что НОД(24, 36) = 12.
Чтобы найти НОК, можно использовать формулу: НОК(a, b) = (a * b) / НОД(a, b). Используя эту формулу и найденное ранее значение НОД(24, 36) = 12, мы получаем НОК(24, 36) = (24 * 36) / 12 = 72.
Теперь, когда вы знаете, как найти НОД и НОК, вы можете легко решать задачи, связанные с числами. Например, вы можете использовать эти знания для нахождения общего времени при встрече, для расчета количества карандашей, которое можно упаковать в коробку, и многого другого. Практикуйтесь и у вас все получится!
Что такое НОД

Для понимания НОД важно знать понятие делителя. Делитель - это число, на которое другое число делится без остатка. Например, делители числа 12 - это 1, 2, 3, 4, 6 и 12. Делители числа 8 - это 1, 2, 4 и 8. Общие делители чисел 12 и 8 - это 1, 2 и 4. НОД чисел 12 и 8 равен 4, так как это наибольший общий делитель этих чисел.
НОД может быть полезен в различных моментах. Например, при упрощении дробей НОД числителя и знаменателя позволяет убрать общие делители и сократить дробь. Также НОД используется для решения некоторых задач в компьютерной науке, алгоритмах и криптографии.
Что такое НОК

Наименьшим общим кратным (НОК) двух или более чисел называется наименьшее число, которое делится на все эти числа без остатка. НОК нескольких чисел можно найти, используя разложение чисел на простые множители.
Для нахождения НОК следует:
- Разложить каждое число на простые множители.
- Записать все простые множители с максимальной степенью, которая встречается в разложениях.
- Домножить все простые множители вместе.
Например, для чисел 4 и 6:
4 = 2^2, 6 = 2 * 3
Максимальная степень простого множителя 2 равна 2, а для простого множителя 3 равна 1.
НОК(4, 6) = 2^2 * 3 = 12.
Таким образом, наименьшим общим кратным для чисел 4 и 6 является число 12.
Как найти НОД двух чисел

Существует несколько способов нахождения НОД двух чисел. Рассмотрим самый простой и широко используемый метод - метод деления.
- Выберите два числа, для которых требуется найти НОД.
- Разделите большее число на меньшее. Если остаток равен нулю, то меньшее число является НОД.
- Если остаток не равен нулю, то повторите шаг 2, но на этот раз поделите предыдущее делитель на полученный остаток.
- Продолжайте повторять шаг 3, пока остаток не станет равным нулю.
- Меньшее число на последнем шаге является НОД заданных чисел.
Таким образом, используя метод деления, можно легко найти НОД двух чисел. Этот метод является основой для различных математических алгоритмов и может быть использован для решения различных задач, включая нахождение наименьшего общего кратного (НОК) двух чисел.
Как найти НОК двух чисел
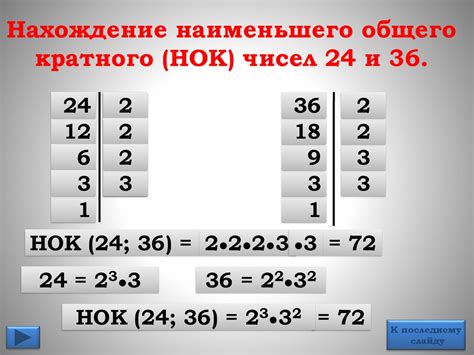
Для нахождения НОК двух чисел можно воспользоваться следующим алгоритмом:
- Найдите наибольший общий делитель (НОД) двух чисел с помощью алгоритма Евклида. НОД можно найти путем последовательного деления большего числа на меньшее с вычислением остатка. Продолжайте делать это до тех пор, пока остаток не станет равным нулю. НОД - это последнее ненулевое число, которое было использовано для деления.
- Найдите НОК с использованием формулы: НОК = (число1 * число2) / НОД. Умножьте два числа и разделите их на значение НОД, чтобы получить НОК.
Применяя этот алгоритм, вы сможете быстро находить НОК двух чисел и использовать его в дальнейших математических расчетах.
Как найти НОД и НОК для трех чисел

Чтобы найти наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) трех чисел, нужно следовать этим простым шагам:
Шаг 1: Запишите три числа, для которых вы хотите найти НОД и НОК.
Шаг 2: Найдите все простые делители каждого числа. Простые числа - это числа, которые делятся только на себя и на 1.
Шаг 3: Запишите все простые делители каждого числа в виде основания степени. Например, если число 12, то его простые делители - это 2 и 3. Записываем как 2^2 * 3^1.
Шаг 4: Для каждого простого делителя выберите наибольшую встречаемость основания степени. Например, для числа 12, наибольшая встречаемость базового показателя 2 - это 2^2. Делаем то же самое для чисел 2 и 3.
Шаг 5: Для НОД умножаем все выбранные простые делители вместе. В нашем примере, НОД - это 2^2.
Шаг 6: Для НОК умножьте все числа вместе, поднесенные к наибольшим встречаемостям основной степени. В нашем примере, НОК - это 2^2 * 3^1.
Итак, теперь вы знаете, как найти НОД и НОК для трех чисел. Удачи вам в решении математических задач!
Пример задачи на нахождение НОД и НОК

Для решения этой задачи, нужно найти НОД (наибольший общий делитель) чисел 3 и 4. Есть несколько способов найти НОД, один из которых – использовать алгоритм Евклида.
Согласно алгоритму Евклида, НОД двух чисел можно найти следующим образом:
- Делим большее число на меньшее. Если остаток от деления равен 0, то НОД равен меньшему числу.
- Если остаток от деления не равен 0, то заменяем большее число на остаток от деления и повторяем шаг 1.
- Повторяем шаги 1 и 2 до тех пор, пока не получим остаток от деления, равный 0. Тогда НОД равен последнему ненулевому остатку от деления.
Применяя алгоритм Евклида к числам 3 и 4, получаем:
- Делим 4 на 3. Остаток равен 1.
- Делим 3 на 1. Остаток равен 0.
Последний ненулевой остаток равен 1, поэтому НОД чисел 3 и 4 равен 1.
Теперь, чтобы найти НОК (наименьшее общее кратное) чисел 3 и 4, можем воспользоваться следующей формулой: НОК = (3 * 4) / НОД.
Возвращаясь к задаче, чтобы хорошо вручить каждому ребенку одинаковое количество апельсинов, нужно заминивать апельсины в количестве НОК, то есть (3 * 4) / 1 = 12.
Таким образом, для того чтобы хорошо вручить каждому ребенку одинаковое количество апельсинов, нужно заминивать 12 апельсинов.
Зачем нужно знать НОД и НОК

Знание НОД необходимо, чтобы решать задачи, связанные с дробями. Например, при сокращении простых или сложных дробей до несократимого вида, нужно найти их НОД и поделить числитель и знаменатель на него.
Также знание НОД позволяет определить, могут ли два или более числа быть делителями друг друга. Если НОД двух чисел равен единице (то есть они взаимно просты), то они не имеют общих делителей, кроме самой единицы. Это свойство используется для определения взаимной простоты чисел.
Знание НОК также имеет важное значение. НОК позволяет решать задачи, связанные с переводом дробей в общий знаменатель или сравнением периодических десятичных дробей. Зная НОК, можно определить, через сколько времени два события произойдут одновременно или когда они снова совпадут.
Благодаря использованию НОД и НОК, ученики 6 класса смогут решать задачи на разложение чисел на простые множители, построение наибольшего и наименьшего общего кратного, а также разбор простых и сложных дробей.
Как применять НОД и НОК в реальной жизни

1. Планирование соревнований
Представьте, что вы организуете спортивные соревнования, в которых участвуют различные команды. Вы должны расставить команды по разным игровым полям так, чтобы они не мешали друг другу и все игры начинались одновременно. Здесь НОК пригодится вам для определения минимального времени, через которое все команды будут готовы к игре.
2. Покупка обоев
Вы решили обновить интерьер своего дома и купить обои, чтобы они покрывали все стены в комнате. У вас есть несколько вариантов обоев разного размера. Вы хотите купить только один тип обоев и при этом использовать их эффективно. Здесь НОД поможет вам определить наибольший общий делитель длин стен и выбрать обои подходящих размеров, чтобы избежать излишков или недостаточности.
3. Расчет времени
Когда вы планируете встречу или поездку, вам может понадобиться рассчитать, через сколько времени ваши часы показывают одинаковое время. Есть несколько простых шагов: определить НОК времени на часах, заметить, когда нажать на кнопку синхронизации или начать движение между двумя точками, и дождаться, пока часы покажут одно и то же время. НОД и НОК помогут вам скоординировать время с друзьями или родственниками.
Это только некоторые примеры использования НОД и НОК в реальной жизни. Помните, что эти понятия могут быть полезными не только в математике, но и в повседневных ситуациях. Имея понимание НОД и НОК, вы сможете легче решать различные задачи и применять их в практических ситуациях.