Нулевая точка функции - это значение аргумента, при котором значение самой функции равно нулю. Найти нулевую точку имеет огромное практическое значение, особенно в науке и технике. Существует множество методов для нахождения нулевой точки функции, и в данной статье мы рассмотрим некоторые из них.
Один из самых простых и широко используемых методов - это графический метод. Он заключается в построении графика функции и определении точки пересечения графика с осью абсцисс (ось, на которой значение функции равно нулю). Однако этот метод требует некоторой интуиции и может быть неприменим в случае сложных функций.
Более точным и эффективным методом является метод ньютона-рафсона. Он основан на итеративном процессе и использует формулу приближенного нахождения нулевой точки. Этот метод требует использования производной функции, поэтому применим только для функций, дифференцируемых на всей своей области определения.
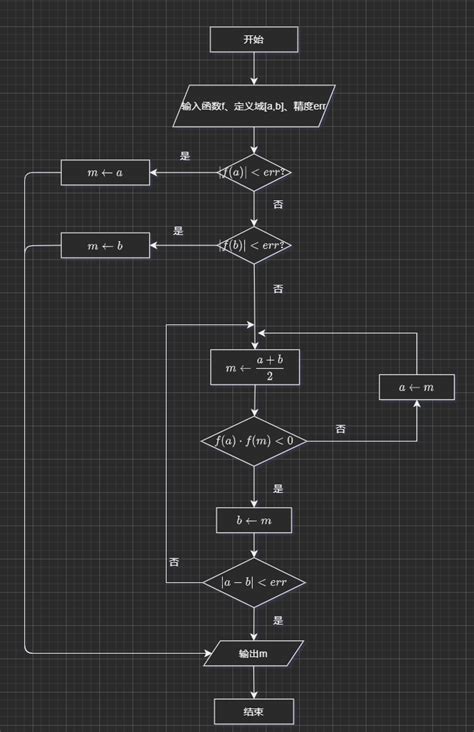
Еще одним методом нахождения нулевой точки функции является метод деления отрезка пополам. Этот метод основан на непрерывности функции и процессе деления отрезка на две равные части. На каждой итерации алгоритма выбирается половина отрезка, на которой значение функции имеет разные знаки, и происходит повторное деление этого отрезка пополам. Такой процесс продолжается до тех пор, пока не будет достигнута заданная точность.
Что такое нулевая точка функции?
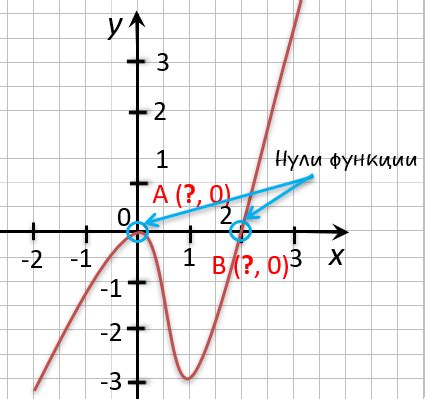
Нулевая точка функции, также известная как корень функции или решение уравнения, представляет собой значение аргумента, при котором функция равна нулю. Иными словами, это точка на графике функции, где она пересекает ось абсцисс.
Нулевая точка функции имеет большое значение для математического анализа и решения уравнений. Найдя все нулевые точки функции, мы можем определить ее поведение, находясь выше или ниже оси абсцисс. Кроме того, нулевые точки функции могут помочь в решении задач и определении значений параметров.
Для поиска нулевых точек функции применяются различные методы, такие как графический, итерационный и аналитический методы. Графический метод заключается в построении графика функции и определении его пересечений с осью абсцисс. Итерационный метод основан на последовательном подборе значений аргумента до тех пор, пока функция не станет близкой к нулю. Аналитический метод включает использование алгебраических и тригонометрических преобразований для нахождения нулевых точек.
Важно отметить, что функция может иметь одну или несколько нулевых точек, а также может не иметь нулевых точек вовсе. Если функция не пересекает ось абсцисс, то у нее нет нулевых точек. В некоторых случаях нулевая точка может быть выражена в виде явной формулы, а в других случаях может потребоваться численный метод для ее нахождения.
Нулевые точки функции играют важную роль в различных областях математики и её приложениях. Они помогают в решении уравнений, определении значений переменных и анализе поведения функций. Поэтому знание о нулевых точках функции является важной составляющей в изучении и применении математики.
Методы приближенного нахождения нулевой точки функции

- Метод деления отрезка пополам - метод, основанный на принципе интервального деления отрезка. Он используется для нахождения нулевых точек функции на отрезке, на котором функция меняет знак. Метод заключается в делении отрезка пополам и проверке знака функции в полученных точках. Процесс продолжается до тех пор, пока не будет достигнута заданная точность.
- Метод Ньютона - метод, основанный на использовании производной функции. Он позволяет приближенно находить нулевые точки функции, используя локальную информацию о поведении функции в окрестности исходной точки. Метод Ньютона основан на итерационной формуле, которая позволяет находить все более близкие приближения к нулевым точкам.
- Метод простой итерации - метод, основанный на преобразовании исходной функции с целью придания ей удобной для вычислений формы. Принцип метода заключается в построении итерационной последовательности, каждый элемент которой строится на основе предыдущего, сходящейся к нулевой точке функции. Этот метод часто применяется в задачах, где производная функции сложно вычислить или не существует.
Каждый из этих методов имеет свои особенности и преимущества. Выбор конкретного метода зависит от характера функции, наличия или отсутствия производной, а также от требуемой точности нахождения нулевой точки. Использование разных методов может быть эффективным при решении различных задач.
Итерационные методы

Основная идея итерационных методов заключается в следующем. Пусть дана функция f(x), у которой требуется найти нулевую точку. Начиная с некоторого начального приближения x₀, мы можем построить последовательность приближений x₁, x₂, ..., xₙ, такую что:
x₁ = g(x₀)
x₂ = g(x₁)
...
xₙ = g(xₙ₋₁)
где g(x) - некоторая функция, представляющая собой преобразование исходного приближения.
На каждой итерации мы находим новое приближение, которое ближе к нулевой точке функции. Процесс продолжается до тех пор, пока не будет достигнута необходимая точность или выполнено другое условие остановки.
Итерационные методы широко используются в численном анализе и оптимизации функций. Некоторые из наиболее известных итерационных методов включают метод простой итерации, метод Ньютона и метод секущих.
Важно отметить, что успех итерационных методов во многом зависит от выбора начального приближения и функции преобразования g(x). Некорректный выбор может привести к расходимости метода или к сходимости к неправильному решению.
Итерационные методы являются мощным инструментом для нахождения нулевых точек функции, однако требуют тщательного анализа и выбора параметров для достижения точных и надежных результатов.
Метод деления отрезка пополам
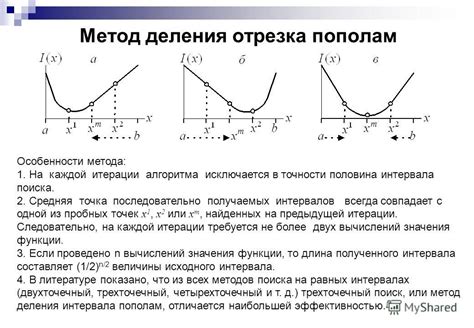
Для применения метода деления отрезка пополам необходимо знать начало и конец отрезка, на котором предполагается нахождение нулевой точки. Затем отрезок делится пополам, находится значение функции в середине и в одном из концов нового отрезка. Если знаки значений функции на концах отрезка различны, то нулевая точка находится на этом отрезке. В противном случае, отрезок с нулевой точкой находится на другом конце и процесс деления повторяется. Этот процесс продолжается до достижения требуемой точности или заданного количества итераций.
Метод деления отрезка пополам достаточно прост в реализации и обладает гарантированной сходимостью. Однако, для некоторых функций и отрезков, он может работать медленнее, чем другие методы. Важным параметром является выбор начального отрезка, так как от этого зависит количество итераций для достижения требуемой точности.
Метод Ньютона

Идея метода Ньютона заключается в следующем: мы начинаем с предполагаемого значения нулевой точки и находим уравнение касательной линии к графику функции в этой точке. Затем мы находим пересечение касательной с осью абсцисс, получая новое приближение к нулевой точке. Этот процесс повторяется до достижения заданной точности.
Для использования метода Ньютона нам необходимо знать производную функции, так как он использует ее для нахождения уравнения касательной линии. Кроме того, метод Ньютона может сходиться только если начальное приближение достаточно близко к нулевой точке, иначе он может расходиться или давать неверные результаты.
В своей основе, метод Ньютона является итерационным процессом, который требует многократных вычислений и обновлений значения приближения. Несмотря на это, метод Ньютона является одним из наиболее эффективных методов нахождения нулевой точки функции с высокой точностью.
Метод простой итерации

Данная последовательность вычисляется с помощью простой формулы:
xn+1 = g(xn), где g(x) – функция, с которой связано уравнение f(x) = 0.
В методе простой итерации важным условием является то, что g(x) должна быть сжимающим отображением на заданном интервале.
Процесс итерации продолжается до тех пор, пока значение xn+1 – xn не станет достаточно малым или пока не будет достигнута заданная точность.
Метод простой итерации может быть эффективен при наличии достаточно гладкой функции и корень находится близко к начальному приближению.
Однако, этот метод имеет свои недостатки. В некоторых случаях решение может не сходиться, и необходимо использовать другие численные методы для поиска нулевой точки функции.
Метод секущих
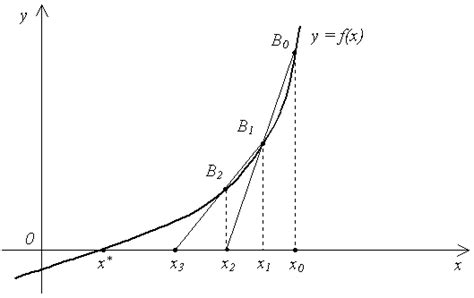
Для использования метода секущих необходимо задать две начальные точки x0 и x1, которые будут являться приближением к нулевой точке. Затем производится итерационный процесс, в котором вычисляются промежуточные точки xn по следующей формуле:
xn = xn-1 - f(xn-1) * (xn-1 - xn-2) / (f(xn-1) - f(xn-2))
Итерационный процесс продолжается до тех пор, пока разность между xn и xn-1 не станет меньше заданной точности.
Метод секущих является одним из гибких и эффективных численных методов для нахождения нулевых точек функции, особенно при сложных или нелинейных функциях. Однако, в отличие от метода Ньютона, он не гарантирует сходимость и может давать разные результаты в зависимости от выбора начальных точек.
Приемы оптимизации процесса поиска нулевой точки функции
Ниже представлены несколько приемов, которые могут помочь оптимизировать процесс поиска нулевой точки функции:
1. Метод бисекции: Этот метод основан на применении промежуточных значений функции для сужения интервала, в котором находится нулевая точка. На каждом шаге процесса интервал сужается в два раза, что приводит к быстрому приближению к нулевой точке.
2. Метод Ньютона: Этот метод использует линейную аппроксимацию функции в окрестности текущей точки для нахождения следующей точки. Это позволяет быстро приближаться к нулевой точке, особенно если начальное приближение достаточно близко.
3. Метод секущих: Этот метод является обобщением метода Ньютона для случая, когда производная функции недоступна или сложна для вычисления. Вместо этого используются две начальные точки для аппроксимации производной и нахождения следующей точки.
4. Метод последовательных приближений: Этот метод основан на последовательном приближении к нулевой точке функции с использованием итераций. На каждом шаге процесса выбирается новая точка, основанная на предыдущей точке, что позволяет приближаться к нулевой точке с любой заданной точностью.
Выбор оптимального метода зависит от конкретной задачи и условий поиска нулевой точки функции. Иногда может потребоваться использование комбинации нескольких методов, чтобы достичь наилучшего результата.
Использование начального приближения

Использование начального приближения позволяет сузить область поиска и ускорить процесс нахождения нулевой точки. Чем ближе начальное приближение к искомой точке, тем быстрее будет достигнута точность решения.
Одним из способов выбора начального приближения является анализ функции и графика. Необходимо произвести предварительную оценку положения нулевой точки, опираясь на закономерности поведения функции на графике. Знаки функции в разных областях графика могут намекнуть на примерное положение нулевой точки.
Другим способом выбора начального приближения является использование метода половинного деления. Это метод, при котором исходный интервал разбивается на половины и анализируется знак функции в середине каждого интервала. Если значения функции на концах интервала имеют противоположные знаки, то нулевая точка находится где-то внутри интервала.
Использование начального приближения - это важное средство в арсенале методов и приемов поиска нулевой точки функции. Правильно выбранное начальное приближение может значительно ускорить процесс нахождения решения, сделать его более точным и эффективным.