Наверняка каждый из нас хотя бы раз в жизни сталкивался с требованием найти сторону треугольника, используя синус и сторону. Этот метод является очень полезным и широко применяемым в различных областях науки, инженерии и архитектуры. В данной статье мы рассмотрим основные принципы нахождения стороны треугольника через синус и сторону, а также приведем несколько примеров для лучшего понимания.
Прежде чем мы погрузимся в детали, давайте вспомним некоторые основные определения. В треугольнике существуют три стороны и три угла. Противоположные стороны называются противолежащими углам. Очень важно помнить, что в треугольнике синус угла определяется отношением противолежащей стороны к гипотенузе.
Для нахождения стороны треугольника через синус и сторону необходимо применить основное тригонометрическое соотношение - теорему синусов. Это соотношение устанавливает, что отношение синуса угла к противолежащей стороне равно отношению синуса соседнего угла к соседней стороне. Данное соотношение позволяет нам находить сторону треугольника через синус и сторону, если известны значения синуса и длины противолежащей стороны.
Определение треугольника и его сторон
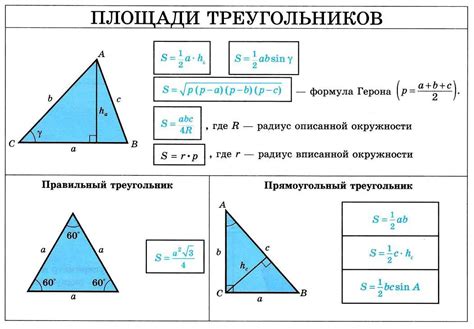
1. Треугольник имеет три стороны, которые могут быть различной длины.
2. Длины сторон треугольника обозначаются обычно буквами a, b и c.
3. Углы треугольника обозначаются прописными буквами A, B и C. Угол A находится напротив стороны a, угол B - напротив стороны b, угол C - напротив стороны c.
4. Сумма всех углов треугольника равна 180 градусам. То есть, A + B + C = 180°.
5. Треугольник может быть разделен на два прямоугольных треугольника. В прямоугольном треугольнике один из углов равен 90°.
6. Для определения треугольника достаточно знать длины любых двух сторон и значение угла, образованного этими сторонами. Этот случай называется "Задачей об определении треугольника по двум сторонам и углу между ними".
Связь между синусом угла и соответствующей стороной треугольника
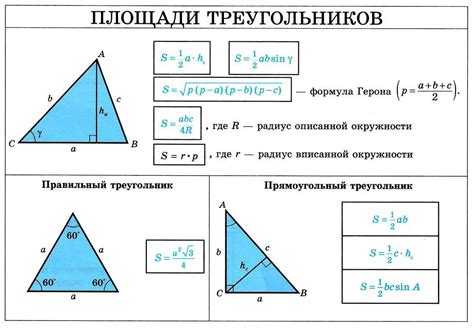
Допустим, у нас есть треугольник ABC. Угол A равен α, сторона AB имеет длину a, а гипотенуза AC равна c. Тогда синус угла α можно записать как sin(α) = a/c.
Используя данное уравнение, мы можем выразить длину противоположной стороны AB через известные значения синуса и гипотенузы: a = c * sin(α).
Таким образом, если нам даны значения угла α и гипотенузы c, мы можем определить длину стороны AB, используя формулу a = c * sin(α).
Аналогично, синус угла можно использовать для определения длины противоположной стороны катета в прямоугольном треугольнике.
Использование синуса угла и известной длины стороны позволяет нам находить длины сторон треугольника и решать различные геометрические задачи, связанные с треугольниками.
Практическое применение формулы нахождения стороны через синус и сторону
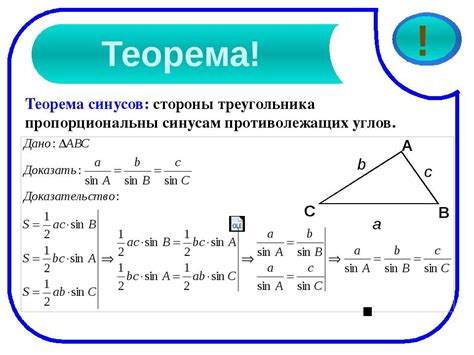
Применение данной формулы может быть очень полезно в различных областях, например в геометрии, строительстве, физике и других науках, где треугольники являются основными элементами. Зная данные о двух сторонах треугольника и угле между ними, можно легко вычислить длину третьей стороны, что часто требуется при решении практических задач.
Для применения формулы достаточно знать значение синуса угла между известной стороной и неизвестной стороной, а также значение известной стороны. Затем следует подставить эти значения в формулу и вычислить результат.
| Известная сторона | Синус угла | Неизвестная сторона |
|---|---|---|
| a | sin(α) | b |
Например, предположим, что у нас есть треугольник, у которого известна одна сторона длиной 5 единиц и угол между этой стороной и неизвестной стороной равен 30 градусов. Чтобы найти длину неизвестной стороны, мы можем использовать формулу:
b = a / sin(α)
b = 5 / sin(30°)
Вычисляя значение синуса 30 градусов (sin(30°) = 0.5), получим:
b = 5 / 0.5 = 10
Таким образом, длина неизвестной стороны треугольника равна 10 единицам.
Как видно из примера, формула нахождения стороны через синус и сторону является простым и эффективным инструментом для решения задач связанных с треугольниками. Ее использование позволяет проводить вычисления без необходимости измерения углов и сторон самостоятельно, что значительно экономит время и силы при решении практических задач.
Примеры нахождения стороны треугольника по заданным данным
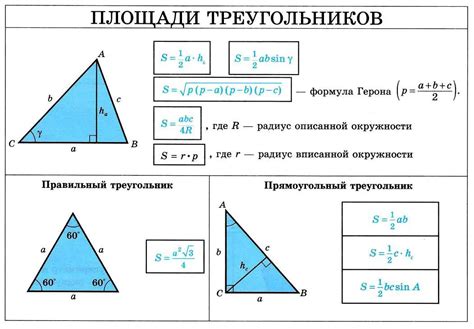
Пример 1:
Дан треугольник ABC, где AC = 5 см и угол BAC = 60 градусов. Необходимо найти сторону AB.
Для начала, обратимся к теореме синусов:
Теорема синусов:
В любом треугольнике отношение длины стороны к синусу противолежащего ей угла равно одному и тому же числу.
Согласно теореме синусов, для нахождения стороны AB, мы можем использовать следующую формулу:
AB / sin(BAC) = AC / sin(BCA)
Заменим известные значения и найдем неизвестное:
AB / sin(60) = 5 / sin(BCA)
AB = (5 * sin(60)) / sin(BCA)
Теперь, чтобы найти значение sin(BCA), мы можем использовать формулу:
sin(BCA) = sin(180 - (BAC + BCA))
Заменим известные значения и найдем sin(BCA):
sin(BCA) = sin(180 - (60 + BCA))
Найденное значение sin(BCA) подставляем в предыдущую формулу и находим сторону AB:
AB = (5 * sin(60)) / sin(BCA)
Подставив конкретное значение sin(BCA) в формулу, можно получить численное значение для стороны AB.
Пример 2:
Дан треугольник XYZ, где XY = 10 см и угол YXZ = 45 градусов. Необходимо найти сторону YZ.
Аналогично предыдущему примеру, мы можем использовать теорему синусов:
YZ / sin(YXZ) = XY / sin(YZX)
Заменим известные значения и найдем неизвестное:
YZ / sin(45) = 10 / sin(YZX)
YZ = (10 * sin(45)) / sin(YZX)
Значение sin(YZX) можно найти аналогичным образом:
sin(YZX) = sin(180 - (YXZ + YZX))
Подставляем найденное значение sin(YZX) в формулу и находим сторону YZ:
YZ = (10 * sin(45)) / sin(YZX)
Аналогично, подставив конкретное значение sin(YZX), можно получить численное значение для стороны YZ.
Расчет стороны треугольника через синус и сторону в специализированных программах и сервисах
Такие программы и сервисы предоставляют пользователю возможность ввести известные значения сторон и синусов углов треугольника и автоматически расчитывают неизвестные стороны. Это удобно, когда требуется найти сторону треугольника быстро и точно без необходимости выполнения сложных математических вычислений вручную.
Программы и сервисы для расчета сторон треугольника через синус и сторону доступны как в виде десктопных приложений, так и в виде онлайн-конвертеров. Они обычно предлагают удобный интерфейс, где пользователь может ввести известные значения и получить результат в кратчайшие сроки.
Пользуясь такими программами и сервисами, можно значительно сократить время и усилия при решении задач, связанных с треугольниками и синусами. Более того, эти инструменты позволяют избежать ошибок, которые могут возникнуть при ручных вычислениях.
Если требуется регулярно решать задачи, связанные с расчетом сторон треугольников через синусы и стороны, использование специализированных программ и сервисов становится особенно полезным. Они помогут сэкономить время и обеспечить точность вычислений, что является важным в математических и инженерных расчетах.
Важные советы и рекомендации по использованию формулы для нахождения стороны треугольника через синус и сторону

Когда вы знаете угол, противолежащий неизвестной стороне, и синус этого угла, вы можете использовать следующую формулу:
Сторона = (Синус угла * Другая сторона) / Синус известного угла
Следующие советы помогут вам использовать эту формулу эффективно и получить точные результаты:
- Выберите правильные единицы измерения: При использовании формулы необходимо убедиться, что все значения, которые вы используете, имеют одни и те же единицы измерения. В противном случае результаты могут быть неправильными.
- Убедитесь в правильном выборе угла: Используя формулу, важно выбрать правильный угол и синус этого угла. Подумайте, какой угол противолежит неизвестной стороне и используйте его синус в формуле.
- Будьте внимательны к знаку: Когда вы подставляете значения в формулу, обратите внимание на знаки синуса и других величин. Используйте правильный знак, чтобы не получить неправильный результат.
- Проверьте результаты: После использования формулы, рекомендуется проверить полученные значения. Если результаты выглядят странными или не соответствуют ожидаемым значениям, проверьте все величины и единицы измерения снова.
Правильное использование формулы для нахождения стороны треугольника через синус и сторону может существенно облегчить геометрические вычисления. Следуя вышеуказанным советам, вы сможете получить точные результаты и успешно решать задачи, связанные с треугольниками.