Линейная функция - одно из важных понятий алгебры, с которым приходится сталкиваться каждому школьнику. Основным свойством линейной функции является ее подобие графиков с прямой линией. Однако, существует особый случай, когда график линейной функции имеет форму гиперболы. В таких случаях необходимо найти коэффициент k по графику этой гиперболы.
Коэффициент k в линейной функции определяет наклон прямой линии на графике. Чтобы найти его по графику гиперболы, нужно учитывать, что вершина этой гиперболы находится в точке с координатами (0, k). Таким образом, коэффициент k можно определить, проведя прямую через вершину гиперболы и проходящую через какую-либо точку на графике функции.
Для нахождения коэффициента k в линейной функции по графику гиперболы рассмотрим пример. Пусть дан график функции y = kx + b, где k и b - неизвестные коэффициенты. Нам даны координаты двух точек A (x1, y1) и B (x2, y2), через которые проходит график гиперболы. Подставив координаты точек в уравнение функции, мы получим два уравнения с двумя неизвестными k и b. Решив эти уравнения, найдем искомый коэффициент k.
Как найти коэффициент k в линейной функции
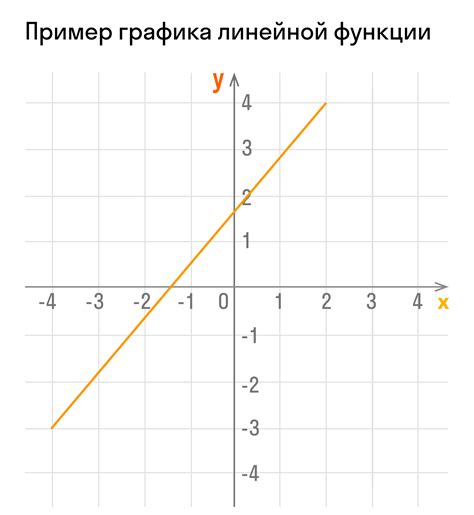
Линейная функция представляет собой прямую на графике с углом наклона, который определяется коэффициентом k. Этот коэффициент отвечает за изменение значения функции с каждым шагом по оси x.
Чтобы найти значение коэффициента k, необходимо воспользоваться формулой y = kx + b, где y - значение функции, х - значение аргумента, b - коэффициент сдвига функции по оси y.
Существуют несколько способов определить значение коэффициента k:
- Если у вас есть две точки на графике функции, вы можете воспользоваться их координатами. Зная значение x и y для обеих точек, можно использовать формулу k = (y2 - y1) / (x2 - x1), чтобы найти значение коэффициента k.
- Если у вас есть уравнение прямой в другой форме, например, y = mx + c, где m - тоже является коэффициентом наклона, то коэффициенты k и m связаны формулой k = m.
Пример:
| x | y |
|---|---|
| 1 | 3 |
| 2 | 6 |
Из таблицы видим, что при значении x = 1, y = 3, а при x = 2, y = 6. Используя формулу из первого способа, найдем значение коэффициента k:
k = (6 - 3) / (2 - 1) = 3
Таким образом, в данном примере значение коэффициента k равно 3.
График гиперболы: инструкция и примеры
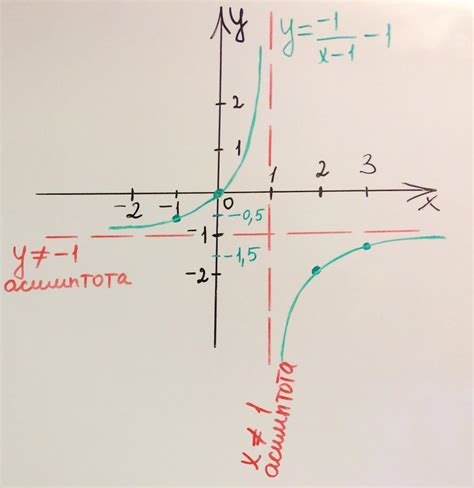
Для нахождения значения k в линейной функции по графику гиперболы необходимо:
Шаг 1: Изучить график гиперболы и определить, какие данные известны. График гиперболы имеет уравнение вида: y = k/x, где k - константа.
Шаг 2: Найти пару координат точки на графике гиперболы. Это может быть любая точка на одной из ветвей гиперболы.
Шаг 3: Подставить найденные координаты точки в уравнение гиперболы. Полученное уравнение будет иметь вид: y = k/x. Необходимо решить полученное уравнение относительно k.
Пример:
Пусть на графике гиперболы известны координаты точки (2, 4). Подставим эти значения в уравнение гиперболы y = k/x:
4 = k/2
Умножим обе стороны уравнения на 2:
8 = k
Таким образом, значение k в линейной функции равно 8.
Используя описанную выше инструкцию и пример, можно найти значение k в любой линейной функции, заданной гиперболой.
Определение линейной функции и графика гиперболы
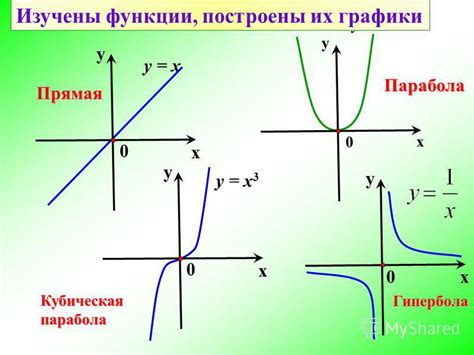
График линейной функции представляет собой прямую линию на плоскости, которая проходит через две точки: точку пересечения с осью y и точку (1, k+b), где k+b - значение функции при x=1.
Гипербола - это кривая, которая описывается уравнением вида y = k/x, где k - постоянное значение. График гиперболы состоит из двух ветвей, которые стремятся к асимптотам, вертикальной и горизонтальной. Асимптоты - это прямые, которые график приближается к бесконечности.
| Линейная функция | Гипербола |
|---|---|
 |  |
Для определения значения k в линейной функции по графику гиперболы можно использовать свойство, что наклон асимптоты графика гиперболы равен коэффициенту k в уравнении линейной функции. Для этого нужно найти две точки, через которые проходят асимптоты гиперболы, и определить их координаты. Затем можно использовать формулу для нахождения наклона прямой, проходящей через эти точки, чтобы получить значение k.
Например, если асимптоты гиперболы проходят через точки (1, 2) и (3, 4), то для определения значения k нужно использовать формулу: k = (y2 - y1) / (x2 - x1) = (4 - 2) / (3 - 1) = 2 / 2 = 1.
Таким образом, значение k в линейной функции будет равно 1.
Краткое объяснение линейной функции и графика гиперболы
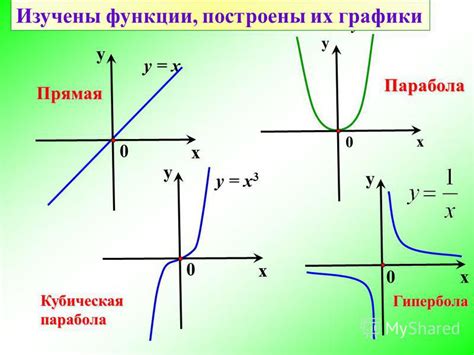
График гиперболы, в свою очередь, представляет собой кривую линию, которая имеет две ветви и асимптоты. Гипербола может быть задана уравнением вида x^2/a^2 - y^2/b^2 = 1 или y^2/b^2 - x^2/a^2 = 1, где a и b - полуоси гиперболы.
Чтобы найти значение k в линейной функции по графику гиперболы, необходимо сначала определить угловой коэффициент наклона одной из ветвей гиперболы. Это можно сделать, измеряя изменение значения y и x на этой ветви. Затем, получив значение углового коэффициента, можно подставить его в уравнение линейной функции y = kx + b вместо k и одного из известных значений x и y. Таким образом, можно найти значение b, а затем и значение k.
Например, если угловой коэффициент наклона гиперболы равен 2 и известны координаты точки (3, 5) на графике, то в уравнение линейной функции можно подставить значения k = 2, x = 3 и y = 5. Таким образом, получаем уравнение 5 = 2 * 3 + b. Решая это уравнение относительно b, можно найти его значение, а затем и значение k.
Таким образом, нахождение значения k в линейной функции по графику гиперболы требует измерения наклона гиперболы и использования этого значения в уравнении линейной функции, вместе с известными значениями x и y. Найденные значения k и b позволяют полностью определить линейную функцию.
Как определить k по графику гиперболы
Определение k в линейной функции, представленной в виде гиперболы, может быть выполнено на основе анализа графика. Чтобы получить значение k, необходимо учитывать следующие шаги:
1. Чтение графика
Изучите график гиперболы, отмечая значения, указанные на осях. Обратите внимание на то, как оси пересекаются и как линия проходит через некоторые точки на графике.
2. Определите координаты двух точек
Выберите две точки на графике гиперболы, где линия пересекает оси координат. Запишите координаты (x, y) каждой точки.
3. Вычислите разницу между y-координатами
Вычислите разницу между y-координатами двух точек, полученных на предыдущем шаге. Обозначим эту разницу как Δy.
4. Вычислите разницу между x-координатами
Вычислите разницу между x-координатами двух точек, полученных на предыдущем шаге. Обозначим эту разницу как Δx.
5. Рассчитайте k
Поделите Δy на Δx, чтобы найти значение k. Формула выглядит следующим образом: k = Δy / Δx.
Например, если у вас есть точки (2, 4) и (6, 2) на графике гиперболы, то Δy равно 4 - 2 = 2 и Δx равно 6 - 2 = 4. Расчет k будет следующим: k = 2 / 4 = 0.5. Таким образом, значение k равно 0.5.
Полученное значение k будет служить коэффициентом для линейной функции, представленной гиперболой. Оно позволяет определить угол наклона линии и влияет на ее поведение и свойства.
Шаги по нахождению коэффициента k

Для нахождения коэффициента k в линейной функции по графику гиперболы следует выполнить следующие шаги:
- Изучите график гиперболы и определите две точки, через которые проходит функция.
- Запишите координаты этих точек в виде (x1, y1) и (x2, y2).
- Используя координаты точек, вычислите вертикальное расстояние между ними (разницу между y-координатами точек).
- Вычислите горизонтальное расстояние между точками (разницу между x-координатами точек).
- Разделите вертикальное расстояние на горизонтальное расстояние, чтобы найти значение коэффициента k (k = Δy / Δx).
Теперь вы знаете, как найти коэффициент k в линейной функции по графику гиперболы. Примените эти шаги к вашим данным и у вас будет значение k, которое можно использовать для определения значения функции для любого заданного x.
Примеры поиска k в линейной функции по графику гиперболы

Когда мы имеем график гиперболы, мы можем найти значение k в соответствующей линейной функции, используя некоторые свойства гиперболы.
Во-первых, помните, что гипербола может быть представлена в виде следующего уравнения:
y = k / x
Где k - это коэффициент, который мы хотим найти.
При изучении графика гиперболы, мы обращаем внимание на два основных свойства:
- График гиперболы имеет две асимптоты, которые являются прямыми линиями, которые указывают направление, в котором график бесконечно стремится приблизиться, но никогда не достигает. Эти асимптоты могут иметь вид y = k / x, где k - это коэффициент.
- График гиперболы также имеет некоторые точки пересечения с осями координат (x, y). Зная значения этих точек, мы можем найти значение k, решив уравнение гиперболы для x = 0 или y = 0.
Давайте рассмотрим примеры:
- Пример 1: График гиперболы пересекает ось x в точке (2, 0) и ось y в точке (0, 4). Чтобы найти k, мы можем решить уравнение гиперболы для x = 0 или y = 0:
- y = k / x
- 0 = k / 2
- k = 0
Значение k в этом примере равно 0.
- Пример 2: График гиперболы пересекает ось x в точке (1, 0) и ось y в точке (0, -3). Решим уравнение гиперболы для x = 0 или y = 0:
- y = k / x
- -3 = k / 1
- k = -3
Значение k в этом примере равно -3.
Таким образом, по графику гиперболы и ее точкам пересечения с осями x и y мы можем найти значение k в соответствующей линейной функции. Важно знать основные свойства гиперболы и использовать их для решения уравнения.
Практические примеры и вычисления

Для нахождения значения параметра k в линейной функции по графику гиперболы, следуйте следующим инструкциям:
- Изучите график гиперболы и определите точки на графике, через которые проходит гипербола.
- Выберите две разные точки на графике, через которые проходит гипербола. Обозначим эти точки как (x1, y1) и (x2, y2).
- Используя координаты этих двух точек, вычислите значение параметра k по формуле: k = (y2 - y1) / (x2 - x1).
- Подставьте найденное значение параметра k в уравнение линейной функции и получите окончательное уравнение функции.
Например, если данные двух точек на графике гиперболы равны (2, 4) и (5, 1), то значение параметра k будет равно:
k = (1 - 4) / (5 - 2) = -3 / 3 = -1.
Таким образом, уравнение линейной функции будет иметь вид y = -x + b, где k = -1 и b - это коэффициент смещения функции.