Физика – это наука, которая изучает природу и ее законы. В ходе проведения различных экспериментов и расчетов, физики часто сталкиваются с необходимостью округления числовых значений. Но что делать, если после округления возникают ошибки? В этой статье мы рассмотрим методы и подходы, которые помогут обнаружить и исправить ошибки округления в физике.
Ошибки округления могут возникать по разным причинам. Одной из основных причин является необходимость ограничения количества знаков после запятой или представление чисел в форме десятичного числа с фиксированной запятой. Кроме того, в некоторых случаях ошибки округления могут возникать из-за некорректного использования методов округления или неправильного понимания самих правил округления.
Для того чтобы обнаружить ошибку округления, необходимо внимательно изучить как само округление, так и особенности конкретных задач физики. Важно знать, какие методы округления используются в программном обеспечении или при проведении экспериментов. Также полезно иметь понимание о проблемах, которые могут возникнуть при округлении чисел, особенно при работе с очень большими или маленькими значениями.
Ошибки округления в физике

В физике, как и в любой другой науке, точность измерений играет важную роль. Однако, при работе с реальными данными неизбежно возникают ошибки округления, которые могут влиять на результаты исследования.
Ошибки округления возникают из-за ограниченности чисел, которые мы используем для представления величин и результатов вычислений. В силу этого, значения могут быть округлены до определенного числа знаков после запятой, что может привести к искажению реального значения.
Для обнаружения ошибок округления в физических расчетах существуют различные методы и подходы. Один из способов - сравнение результатов с теоретическими значениями или значениями, полученными другими методами. Если значения отличаются на значительное количество знаков после запятой, это может указывать на ошибку округления.
Еще один метод - анализ чувствительности результатов к изменениям входных данных. Если небольшое изменение входных значений приводит к большим изменениям в окончательных результатах, это также может указывать на ошибку округления.
Ошибки округления могут быть минимизированы путем использования более точных методов вычислений или увеличения числа знаков после запятой, которые используются при представлении величин. Однако, полностью избежать таких ошибок практически невозможно, поэтому важно учитывать их наличие и искать способы их обнаружения и коррекции.
Значение точности в физике
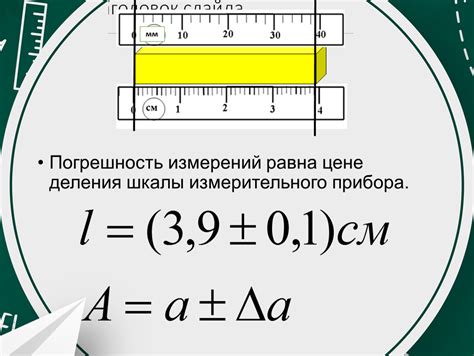
Точность измерений и значений в физике имеет огромное значение. Она определяет степень достоверности результатов экспериментов и расчетов. Физические величины всегда округляются до определенного количества значащих цифр, чтобы учесть погрешности измерений и вычислений.
Определение точности в физике включает в себя понятия абсолютной и относительной погрешностей. Абсолютная погрешность - это разница между измеренным значением и "истинным" значением физической величины. Относительная погрешность выражает отношение абсолютной погрешности к измеренному значению.
Для того, чтобы обнаружить ошибку округления в физике, необходимо внимательно отслеживать значения точности при проведении экспериментов и расчетах. Если после округления значение физической величины слишком сильно отличается от ожидаемого, это может указывать на ошибку округления или другую ошибку в расчетах.
Ошибки округления могут возникать из-за неправильного выбора числа значащих цифр или неправильного применения правил округления. Для уменьшения вероятности таких ошибок, необходимо придерживаться установленных стандартов и использовать правильные методы округления значений.
Помимо этого, следует использовать методы контроля качества измерений, такие как повторные измерения, использование калибровочных стандартов и проверка результатов с использованием известных физических законов.
Важно понимать, что ошибки округления могут быть неизбежными в реальных экспериментах, и они должны быть учтены в анализе и интерпретации результатов. Вместе с тем, обнаружение и исправление таких ошибок помогает повысить точность и надежность физических измерений и расчетов.
Методы обнаружения ошибок округления

Ошибки округления могут возникать в различных физических моделях и вычислениях, и для их обнаружения существуют разные методы. Рассмотрим некоторые из них:
1. Сравнение с аналитическим решением. В некоторых задачах существует аналитическое решение, которое можно использовать для сравнения с численными результатами. Если численное решение существенно отличается от аналитического, возможно, имеет место ошибка округления.
2. Сравнение с более точным численным методом. Если доступны разные численные методы для решения одной и той же задачи, можно сравнить результаты этих методов. Если результаты значительно различаются, это может указывать на ошибку округления.
3. Анализ порядка ошибки. Путем анализа зависимости ошибки от шага численного метода можно определить, какие именно операции приводят к ошибке округления. Если некоторые операции приводят к существенной ошибке округления, их можно скорректировать или заменить более стабильными алгоритмами.
4. Использование большей точности. Если есть подозрение на ошибку округления, можно попробовать увеличить точность вычислений. Например, использовать переменные с плавающей точкой двойной точности вместо одинарной, или увеличить число разрядов, используемых при округлении.
5. Тестирование на простых случаях. Можно провести тесты на простых, хорошо известных случаях, где результаты известны заранее. Если численные результаты значительно отличаются от ожидаемых, возможно, имеет место ошибка округления.
Использование комбинации этих методов позволяет обнаружить и исправить ошибки округления в физических вычислениях, повышая точность и надежность результатов.
Оценка погрешности в экспериментах

Для оценки погрешности в экспериментах используются различные методы. Один из наиболее распространенных методов - метод наименьших квадратов. Он основан на минимизации суммы квадратов отклонений между экспериментальными и теоретическими значениями.
Другой метод - метод статистической обработки данных. Он основан на применении математических статистических моделей для оценки погрешности и достоверности результатов экспериментов. С помощью этого метода можно определить доверительные интервалы и доверительные ошибки измерений.
Также существуют специальные математические формулы для расчета различных видов погрешностей, таких как абсолютная погрешность, относительная погрешность и стандартное отклонение.
- Абсолютная погрешность представляет собой разность между экспериментальным и точным значением величины.
- Относительная погрешность выражается отношением абсолютной погрешности к точному значению величины.
- Стандартное отклонение является мерой разброса результатов эксперимента относительно их среднего значения.
Оценка погрешности в экспериментах является неотъемлемой частью их проведения. Она позволяет ученным оценить достоверность результатов и принять необходимые меры для снижения погрешностей в будущих экспериментах.
Сравнение теоретических и экспериментальных значений
При сравнении теоретических и экспериментальных значений важно учитывать все факторы, которые могут повлиять на точность полученных результатов. Например, погрешность измерений, влияние внешних условий, систематические ошибки и другие факторы.
Для удобства сравнения теоретических и экспериментальных значений можно использовать таблицу. В таблице можно указать значения с разными уровнями точности, а также вычислить разницу между ними. Это позволит легко обнаружить возможные ошибки округления.
| Параметр | Теоретическое значение | Экспериментальное значение | Разница |
|---|---|---|---|
| Масса (кг) | 2.45 | 2.47 | +0.02 |
| Скорость (м/с) | 10.5 | 10.4 | -0.1 |
| Температура (°C) | -20 | -19 | +1 |
В данной таблице приведены примеры параметров, для которых сравниваются теоретические и экспериментальные значения. В последнем столбце указана разница между значениями. Если разница превышает допустимую погрешность, это может свидетельствовать о наличии ошибки округления.
Осуществление сравнения теоретических и экспериментальных значений является важным шагом при обнаружении ошибок округления в физике. Благодаря этому методу можно выявить и исправить возможные неточности и повысить точность представленных результатов.
Программные инструменты для обнаружения ошибок округления

Вот некоторые из таких инструментов:
Пакеты для высокоточных вычислений - такие пакеты, как GNU MPFR и Boost.Multiprecision, предоставляют высокоточные арифметические операции, которые позволяют избежать ошибок округления. Эти инструменты позволяют выполнять вычисления с большей точностью и контролировать округление.
Статический анализатор кода - такие инструменты, как clang-tidy и PVS-Studio, могут помочь обнаружить потенциальные ошибки округления в исходном коде. Эти инструменты анализируют код на наличие ситуаций, которые могут привести к ошибкам округления, и предупреждают о них.
Модули для точных вычислений - некоторые языки программирования предоставляют модули или библиотеки для точных вычислений. Например, в Python есть модуль decimal, который позволяет работать с числами с фиксированной точностью и задавать правила округления. Это может быть полезным при обработке денежных единиц или других ситуаций, требующих точности округления.
Важно помнить, что при использовании этих программных инструментов необходимо учитывать контекст проблемы округления. Ошибки округления могут возникать не только из-за погрешностей в вычислениях, но и из-за неясных правил округления или условий задачи. Поэтому кроме программных инструментов, важно также тщательно анализировать математические модели и условия задачи для предотвращения ошибок округления.
В данной статье были рассмотрены основные причины и методы обнаружения ошибок округления. В первую очередь, для минимизации таких ошибок нужно выбирать подходящий метод округления, учитывая особенности конкретной задачи.
Кроме того, можно использовать различные методы анализа и проверки, такие как сравнение вычислений с аналитическими результатами, анализ чувствительности к изменениям входных данных, многократные вычисления с разными точностями и другие.
Важно учитывать, что ошибки округления нередко накапливаются и могут значительно исказить результаты. Поэтому рекомендуется проводить дополнительные исследования и анализ для проверки точности вычислений.
Наконец, обнаружение ошибок округления является важной частью процесса разработки физических моделей и программ. Это позволяет улучшить точность результатов, повысить надежность вычислений и снизить вероятность возникновения непредвиденных проблем.
Таким образом, понимание причин и методов обнаружения ошибок округления является важной компетенцией для физиков и инженеров, работающих с численными методами. Это помогает обеспечить качество и достоверность получаемых результатов и повысить эффективность научно-исследовательских и инженерных задач.