Сопротивление - одна из основных характеристик электрической цепи. Для многих начинающих электриков и электронщиков понятие сопротивления может показаться сложным и непонятным. Однако, понимание сопротивления и его правильное измерение являются необходимыми навыками для работы с электрическими цепями.

Сопротивление измеряется в омах и указывает на то, насколько сильно цепь препятствует протеканию электрического тока. Чем выше сопротивление, тем меньше ток протекает через цепь. Но как можно найти значение сопротивления в цепи?

Самый простой и распространенный способ измерения сопротивления - использование омметра. Омметр - это прибор, который позволяет измерять сопротивление. Чтобы измерить сопротивление с помощью омметра, необходимо подключить его к цепи. Важно помнить, что измерения сопротивления следует производить при выключенной цепи и отсутствии напряжения.

Раздел 1: Основные понятия о сопротивлении

Сопротивление является интенсивной характеристикой и не зависит от длины и площади поперечного сечения проводника. Зависит только от материала проводника и его геометрии. Чем больше длина и площадь сечения проводника, тем больше сопротивление.

Сопротивление проводников обычно приводится в табличной или удельной форме. Табличное сопротивление указывается для единичной длины проводника, а удельное сопротивление - для проводника единичного сечения. Удельное сопротивление обозначается греческой буквой "ρ" (ро) и измеряется в омах на метр.

Сопротивление проводников зависит не только от их материала и геометрии, но и от температуры. С увеличением температуры сопротивление проводников обычно увеличивается. Поэтому, при расчете сопротивления в цепи, необходимо учитывать температурные условия эксплуатации.

2. Закон Ома и его роль в нахождении сопротивления

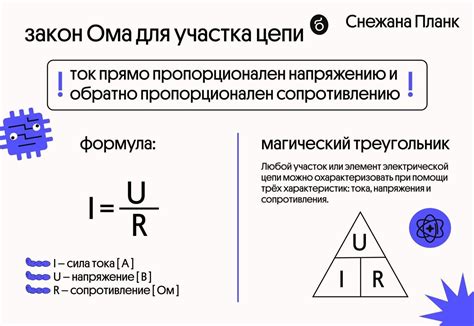
U = I * R

Где:

• U - напряжение в вольтах (В);
• I - сила тока в амперах (А);
• R - сопротивление в омах (Ω).

Закон Ома позволяет между этими тремя величинами установить математическую зависимость. Он помогает понять, как изменение одной величины влияет на другие и облегчает расчет сопротивления в цепи.

Для нахождения сопротивления в цепи, нужно знать величину напряжения и силу тока. Напряжение может быть измерено с помощью вольтметра, а сила тока - с помощью амперметра. Если известны оба значения, сопротивление можно вычислить, используя закон Ома.

Например, при измерении напряжения в цепи, равного 10 В, и известной силе тока, равной 2 А, сопротивление будет:

R = U / I = 10 В / 2 А = 5 Ом

Таким образом, сопротивление в данной цепи составляет 5 омов.

Закон Ома играет ключевую роль в нахождении сопротивления в электрической цепи, а понимание его принципов помогает в работе с электрическими схемами и устройствами.

Раздел 3: Виды сопротивлений в электрических цепях

В электрических цепях сопротивление может быть представлено различными элементами. Здесь мы рассмотрим основные виды сопротивлений:

1. Фиксированное сопротивление

Фиксированное сопротивление имеет постоянное значение и не меняется с течением времени. Оно может быть представлено, например, резистором, который является самым распространенным элементом сопротивления в электронных цепях.

2. Переменное сопротивление

Переменное сопротивление изменяет свое значение в зависимости от входного сигнала или других факторов. Примерами переменных сопротивлений могут служить дроссель, термистор и переменный резистор.

3. Активное и реактивное сопротивление

Активное сопротивление относится к сопротивлению, которое преобразует электрическую энергию в другие формы энергии, такие как тепло или свет. Реактивное сопротивление, с другой стороны, связано с элементами, которые хранят или отдают энергию в электрической цепи, такими как конденсаторы и катушки индуктивности.

4. Сопротивление паразитных элементов

Паразитные элементы сопротивления могут возникать в электрических цепях вследствие нежелательных эффектов, таких как сопротивление проводников и контактов, эффекты скин-эффекта и проникновение магнитного поля.

Знание различных видов сопротивлений позволяет более глубоко понять, как управлять электрическими цепями и решать задачи, связанные с их проектированием и анализом.

Раздел 4: Сопротивление в последовательном соединении

В последовательном соединении сопротивления в цепи соединяются друг за другом, так что электрический ток проходит через них последовательно. Это означает, что общий ток, проходящий через все сопротивления, одинаков для каждого из них.

Для вычисления сопротивления в последовательном соединении необходимо просуммировать значения сопротивлений каждого элемента в цепи. То есть, сопротивление цепи, состоящей из двух сопротивлений R1 и R2, можно найти по формуле:

R = R1 + R2

Если в цепи больше двух сопротивлений, то их сопротивления также просто суммируются для получения общего сопротивления цепи.

Для примера, предположим, что у нас есть цепь с двумя сопротивлениями: R1 = 10 Ом и R2 = 20 Ом. Для определения общего сопротивления нашей цепи, мы просто сложим значения R1 и R2:

R = 10 Ом + 20 Ом = 30 Ом

Таким образом, общее сопротивление этой цепи равно 30 Ом.

Раздел 5: Сопротивление в параллельном соединении

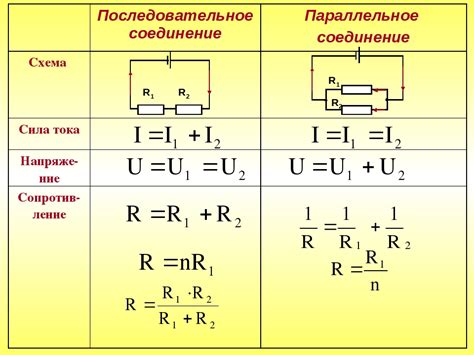
В параллельном соединении сопротивления объединяются таким образом, что они соединяются параллельно друг другу. В этом случае ток делится между сопротивлениями, а напряжение на всех сопротивлениях одинаково.

Для расчета сопротивления в параллельном соединении используется следующая формула:

1 / R_пар = 1 / R₁ + 1 / R₂ + 1 / R₃ + ... + 1 / R_n

• Где R_пар - общее сопротивление в параллельном соединении.
• R₁, R₂, R₃, ..., R_n - сопротивления, соединенные параллельно.

Данная формула позволяет вычислить общее сопротивление в параллельном соединении с любым количеством сопротивлений. Значение общего сопротивления всегда будет меньше наименьшего сопротивления в параллельном соединении.

Для примера, предположим у нас есть параллельное соединение трех сопротивлений: R₁ = 10 Ом, R₂ = 20 Ом и R₃ = 30 Ом. Используя формулу, можно вычислить общее сопротивление:

1 / R_пар = 1 / 10 + 1 / 20 + 1 / 30

1 / R_пар = 3 / 60 + 2 / 60 + 1 / 60

1 / R_пар = 6 / 60

Таким образом, общее сопротивление в данном примере равно 60 / 6 = 10 Ом.

Расчет сопротивления в параллельном соединении может быть полезен для анализа и проектирования электрических цепей. Знание данной формулы позволяет эффективно управлять сопротивлением в цепи и достигать нужных параметров для успешного функционирования электрических устройств.

Раздел 6: Расчет общего сопротивления в сложных цепях

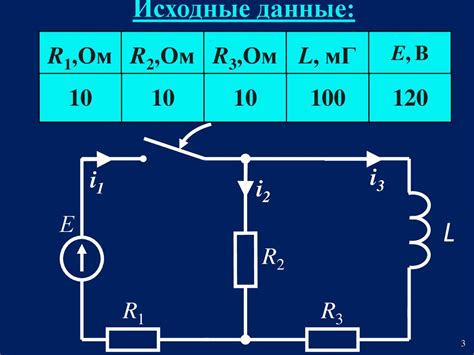
В предыдущих разделах мы изучили, как рассчитывать сопротивление в простых электрических цепях с использованием формул Ома. Теперь давайте перейдем к более сложным случаям, когда в цепи присутствуют соединения последовательно и параллельно.

Когда в цепи присутствуют компоненты, подключенные последовательно, общее сопротивление можно рассчитать путем сложения сопротивлений каждого компонента:

Р_общ = Р₁ + Р₂ + Р₃ + ...

Если же компоненты подключены параллельно, общее сопротивление можно рассчитать с помощью следующей формулы:

1 / Р_общ = 1 / Р₁ + 1 / Р₂ + 1 / Р₃ + ...

При расчете сложных цепей, часто приходится комбинировать соединения последовательно и параллельно. Для этого следует сначала рассчитать сопротивление внутри каждого подсоединения, а затем использовать полученные значения для расчета общего сопротивления.

Например, представим сложную цепь, состоящую из трех резисторов, где два резистора подключены последовательно, а третий резистор подключен параллельно с этой группой. Сначала найдем суммарное сопротивление для резисторов, подключенных последовательно, с помощью формулы Р_общ = Р₁ + Р₂. Затем, используя полученное значение и сопротивление третьего резистора, найдем общее сопротивление всей цепи с помощью формулы 1 / Р_общ = 1 / (Р_1.2) + 1 / Р₃.

Исследование и расчет сложных цепей требует практики и понимания основных принципов электрической цепи. Важно помнить, что сопротивление в цепи может меняться в зависимости от ее конфигурации, и что правильный расчет сопротивления может быть критическим при планировании и проектировании электрических цепей.

Раздел 7: Измерение сопротивления с помощью мультиметра

Чтобы измерить сопротивление с помощью мультиметра, следуйте этим шагам:

• Установите мультиметр в режим измерения сопротивления (обычно обозначается как «Омметр» на переключателе функций).
• Отключите сопротивление, которое вы хотите измерить, от источника питания.
• Подключите один конец сопротивления к «COM»-разъему мультиметра и другой конец к разъему, обозначенному как «V/Ω/мА».
• Осторожно считайте показания с мультиметра. Обычно оно будет отображаться в единицах измерения ома (Ω).

Иными словами, режим измерения сопротивления на мультиметре позволяет вам определить сопротивление электрического элемента или цепи. Это полезно для проверки целостности элементов и идентификации неисправностей.

Раздел 8: Практические примеры расчета сопротивления в цепях

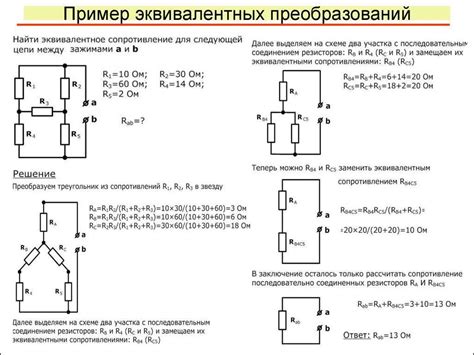
Разобравшись с основными принципами и формулами расчета сопротивления в цепях, давайте рассмотрим несколько практических примеров, чтобы закрепить полученные знания.

Пример 1: Простая цепь сопротивлений

Предположим, у нас есть цепь, состоящая из трех последовательно соединенных сопротивлений: R1 = 10 Ом, R2 = 20 Ом и R3 = 30 Ом.

Для расчета общего сопротивления цепи, мы можем использовать формулу:

Rобщ = R1 + R2 + R3

В нашем случае, общее сопротивление цепи будет:

Rобщ = 10 Ом + 20 Ом + 30 Ом = 60 Ом

Пример 2: Параллельное соединение сопротивлений

Допустим, у нас есть два сопротивления, R1 = 15 Ом и R2 = 25 Ом, которые соединены параллельно.

Для расчета общего сопротивления параллельного соединения, мы можем использовать формулу:

1/ Rобщ = (1/ R1) + (1/ R2)

Сначала найдем сопротивление каждого сопротивления в параллельном соединении:

R1 = 15 Ом

R2 = 25 Ом

Затем найдем общее сопротивление:

1/ Rобщ = (1/ 15 Ом) + (1/ 25 Ом) = (2/ 30 Ом) + (3/ 30 Ом) = 5/ 30 Ом = 1/6 Ом

1/ Rобщ = 1/6 Ом

Rобщ = 6 Ом

Это значит, что общее сопротивление параллельного соединения сопротивлений R1 и R2 равно 6 Ом.

Пример 3: Комбинированное соединение сопротивлений

Рассмотрим цепь, состоящую из последовательно соединенной группы сопротивлений, а затем параллельно соединенной с другой группой сопротивлений.

Допустим, у нас есть две группы сопротивлений:

Группа 1: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом (последовательное соединение)

Группа 2: R4 = 40 Ом, R5 = 50 Ом, R6 = 60 Ом (параллельное соединение)

Для расчета общего сопротивления комбинированного соединения, мы можем сначала рассчитать общее сопротивление каждой группы, а затем рассчитать общее сопротивление всей цепи.

Рассчитаем общее сопротивление группы 1:

Rсумма1 = R1 + R2 + R3

Rсумма1 = 10 Ом + 20 Ом + 30 Ом = 60 Ом

Рассчитаем общее сопротивление группы 2:

1/ Rсумма2 = (1/ R4) + (1/ R5) + (1/ R6)

1/ Rсумма2 = (1/ 40 Ом) + (1/ 50 Ом) + (1/ 60 Ом) = (3/ 120 Ом) + (2/ 100 Ом) + (5/ 300 Ом) = 10/ 300 Ом + 6/ 300 Ом + 5/ 300 Ом = 21/ 300 Ом = 7/ 100 Ом

Rсумма2 = 100/ 7 Ом

Для расчета общего сопротивления комбинированного соединения, мы можем использовать формулу для параллельного соединения сопротивлений, где Rсумма1 и Rсумма2 являются сопротивлениями, соответствующими каждой группе:

1/ Rобщ = (1/ Rсумма1) + (1/ Rсумма2)

Затем найдем общее сопротивление:

1/ Rобщ = (1/ 60 Ом) + (1/ (100/ 7 Ом)) = (7/ 4200 Ом) + (42/ 4200 Ом) = 49/ 4200 Ом = 1/ (4200/ 49) Ом

1/ Rобщ = 1/ (4200/ 49) Ом

Rобщ = (4200/ 49) Ом

Таким образом, общее сопротивление комбинированного соединения сопротивлений группы 1 и группы 2 равно (4200/ 49) Ом.

Используя эти практические примеры, вы можете усовершенствовать свои навыки расчета сопротивления в цепях и применить полученные знания в реальных ситуациях.