Радиус окружности – это расстояние от центра окружности до любой ее точки. Зная длину окружности и длину дуги, можно легко вычислить радиус, используя определенные формулы. Эта навык полезен в геометрии, физике, инженерных расчетах и других областях знаний.
Для того чтобы найти радиус окружности по длине и дуге, нужно знать несколько важных формул:
1. Длина окружности вычисляется по формуле: Длина = 2πR, где R – радиус окружности.
2. Длина дуги вычисляется по формуле: Длина дуги = (дуга/360°) * Длина окружности, где дуга – центральный угол, выраженный в градусах.
Теперь, зная длину окружности и длину дуги, можно легко найти радиус окружности:
1. Вычисляем длину окружности по известной формуле: Длина = 2πR.
2. Из формулы для длины дуги выражаем дугу: Длина дуги = (дуга/360°) * Длина окружности. Здесь нам известны все значения, кроме дуги, и мы можем легко выразить ее.
Таким образом, зная длину окружности и длину дуги, мы можем вычислить радиус окружности. Важно помнить, что формулы, приведенные выше, применимы только в том случае, если окружность является точной и выпуклой.
Что такое радиус окружности?
Радиус окружности играет важную роль в геометрии и математике, так как он является основной величиной при расчете площади, длины дуги и других параметров окружности. От радиуса зависит также кривизна окружности - чем меньше радиус, тем более крутая окружность.
Зная радиус, можно легко определить другие характеристики окружности, такие как длина окружности, площадь круга и длина дуги. Радиус также используется в различных областях науки и техники, например, в физике при рассмотрении вращения тел и в инженерии при проектировании круглых конструкций.
Как найти радиус по длине?

Если известна только длина окружности, можно воспользоваться формулой радиуса окружности:
r = L / (2π)
где r - радиус окружности, L - длина окружности, а π - математическая константа, примерно равная 3.14159.
Другой способ найти радиус - разделить длину окружности на 2π, где π примерно равно 3.14159, а затем извлечь квадратный корень из полученного значения:
r = √(L / (2π))
Эта формула позволяет точнее определить радиус окружности, особенно при больших значениях длины.
Зная радиус окружности, можно выполнять различные геометрические расчеты и конструкции, использовать радиус как основу для формул площади и объема фигур, а также определить другие характеристики окружности.
Формула нахождения радиуса по длине окружности
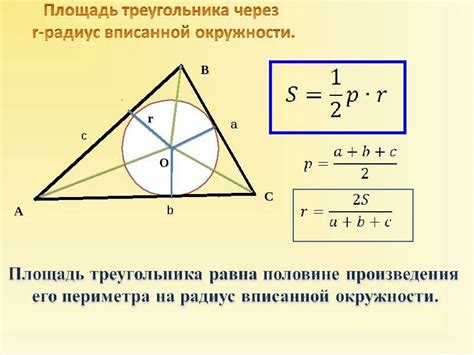
Для нахождения радиуса окружности по её длине можно использовать следующую формулу:
- Найдите длину дуги окружности, измеренную в выбранных единицах измерения. Обозначим её как L.
- Найдите число Пи (π), которое примерно равно 3.14159 и используется для вычисления окружностей. Обозначим его как π.
- Используя формулу, найдите радиус по следующей формуле:
R = L / (2 * π),
где R - радиус окружности.
Данная формула основана на соотношении длины окружности к её радиусу и числу Пи.
Найденный радиус окружности будет измеряться в тех же единицах, что и длина дуги, предоставленная в начальных данных.
Пример расчета радиуса по длине
Допустим, у нас есть дуга окружности длиной 10 метров. Мы хотим найти радиус этой окружности.
Используя формулу, связывающую длину окружности (L) с радиусом (r):
L = 2πr
Мы можем решить эту формулу относительно радиуса, чтобы найти его значение:
r = L / (2π)
Подставим значение длины окружности в формулу:
r = 10 / (2π)
Выполним вычисления:
r ≈ 10 / (2 × 3.14159)
r ≈ 10 / 6.28318
r ≈ 1.59155 метра
Таким образом, радиус окружности, если длина дуги составляет 10 метров, равен примерно 1.59155 метра.
Как найти радиус по дуге?

Для нахождения радиуса окружности по дуге можно воспользоваться специальной формулой, которая основана на взаимосвязи длины дуги с углом, на который она охватывает.
Формула для нахождения радиуса (r) по длине дуги (L) и углу (α) имеет вид:
r = L / α
В этой формуле нам известны длина дуги и угол, на который она охватывает. Для получения радиуса необходимо разделить длину дуги на угол в радианах.
Угол (α) можно выразить с помощью формулы:
α = π * (угол в градусах) / 180
Где π - это математическая константа, примерно равная 3,14159.
Если изначально даны длина дуги (L) и угол (α) в градусах, то для нахождения радиуса (r) необходимо последовательно вычислить значение угла (α) в радианах и подставить значения в формулу.
Таким образом, нахождение радиуса по дуге является достаточно простой задачей при знании соответствующих формул и учетом единиц измерения.
Формула нахождения радиуса по длине дуги и углу
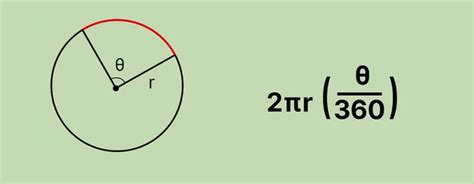
Для нахождения радиуса окружности по длине дуги и углу существует специальная формула. Данная формула позволяет определить радиус окружности, если известна длина дуги и центральный угол, на который эта дуга охватывает.
Формула для нахождения радиуса в данном случае выглядит следующим образом:
Радиус = (длина дуги * 180) / (π * угол)
где:
- Радиус – радиус окружности, который нужно найти;
- Длина дуги – известная длина дуги на окружности;
- угол – центральный угол, на который охватывается дуга.
Эта формула позволяет найти радиус окружности по известным данным длины дуги и центрального угла. Используя эту формулу, вы сможете точно и быстро определить радиус окружности.
Пример расчета радиуса по длине дуги и углу

Для расчета радиуса окружности по известной длине дуги и углу можно использовать следующие формулы:
- Угол в радианах:
θ = длина_дуги / радиус. - Угол в градусах:
θ = (длина_дуги / радиус) * (180 / π). - Радиус:
радиус = длина_дуги / угол_в_радианах.
Давайте рассмотрим пример: у нас есть длина дуги, равная 10 метров, и угол, равный 45 градусов. Чтобы найти радиус окружности, применяем формулу, заданную под номером 3:
Радиус: радиус = 10 / (45 * (π / 180)).
Выполняем вычисления:
Радиус: радиус = 10 / (45 * (3.14159 / 180)) ≈ 6.37.
Таким образом, радиус окружности будет примерно равен 6.37 метров.