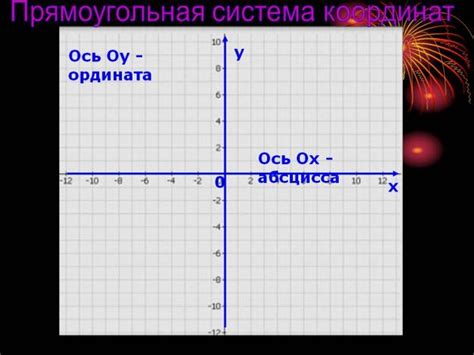
Определение абсциссы точки - одна из основных задач в математике. Абсцисса является одной из координат точки и определяет ее расположение на числовой оси Ox. Важно не только знать, что такое абсцисса, но и уметь ее определять.
Первый способ определения абсциссы точки - это посмотреть на значение, которое она принимает на оси Ox. Если точка расположена левее начала координат (где значения абсциссы отрицательны), то ее абсцисса будет отрицательным числом. Если точка находится правее начала координат (где значения абсциссы положительны), то ее абсцисса будет положительным числом. Если точка находится на оси Ox, то ее абсцисса будет равна нулю. Просто взглянув на положение точки на графике, вы сможете определить ее абсциссу.
Второй способ определения абсциссы точки - это использование формулы. Если у вас есть уравнение прямой, кривой или графика, то вы можете воспользоваться решением этого уравнения для определения абсциссы точки. Если у вас, например, дано уравнение прямой вида y = kx + b, где k и b - известные значения, вы можете вставить значения координат точки в это уравнение и решить его относительно абсциссы. Таким образом, вы сможете определить абсциссу точки на основе уравнения графика.
Абсцисса точки - определение и применение
Для определения абсциссы точки на плоскости можно использовать различные методы. Один из наиболее распространенных способов - это использование формулы координатной плоскости:
x = абсцисса точки
Эта формула позволяет нам найти абсциссу точки, зная ее координаты на плоскости. Например, если у нас есть точка с координатами (3, 2), то абсцисса этой точки равна 3.
Знание абсциссы точки имеет широкое применение в различных областях. Например:
- В физике абсцисса точки может использоваться для определения положения тела или частицы на плоскости или в пространстве.
- В математике абсцисса точки может быть использована для решения геометрических задач и построения графиков функций.
- В программировании абсцисса точки может использоваться для разработки графических интерфейсов и обработки данных.
- В картографии абсцисса точки может использоваться для определения географического положения объекта на карте.
Таким образом, понимание абсциссы точки и ее определение является важным для решения различных задач и применения в различных областях знания.
Математический аппарат
Для определения абсциссы точки существует несколько эффективных способов, которые базируются на математических формулах:
1. Формула координат точки на плоскости: x = x0 + a * t, где x0 - начальная абсцисса точки, a - скорость изменения абсциссы, t - время.
2. Формула прямой: y = kx + b, где k - коэффициент наклона прямой, b - свободный член.
3. Формула суммы абсциссы и ординаты: x = x1 + x2, где x1 и x2 - абсциссы двух точек.
4. Формула средней абсциссы: x = (x1 + x2)/2, где x1 и x2 - абсциссы двух точек.
Навык использования данных формул в алгебре и геометрии позволяет определить абсциссу точки с точностью и эффективностью.
Графический метод построения

Для построения графического метода нужно иметь уравнение функции f(x) и заданный отрезок, в пределах которого будет искаться абсцисса точки.
- Начните с построения осей координат и отметьте на них начало координат.
- Выберите произвольное значение абсциссы x на отрезке, заданном уравнением функции.
- Вычислите соответствующее значение ординаты y, подставив выбранное значение x в уравнение функции.
- Отметьте полученную точку (x, y) на графике.
- Повторите шаги 2-4 для различных значений абсциссы x на заданном отрезке.
- Соедините точки полученными линиями или кривыми, чтобы получить график функции.
- Определите на графике абсциссу точки, которую нужно найти, и считайте её координату.
Графический метод построения является наглядным и позволяет визуально определить абсциссу точки на графике функции. Он широко используется в области математики, физики, экономики и других наук для анализа и решения различных задач.
Аналитическое вычисление
Для аналитического вычисления абсциссы точки можно использовать различные формулы и методы. Одна из самых распространенных формул – формула расстояния между двумя точками на плоскости.
Формула расстояния между двуми точками P1(x1, y1) и P2(x2, y2) на плоскости задается следующим образом:
d = √((x2 - x1)^2 + (y2 - y1)^2)
Используя эту формулу, мы можем определить расстояние между двуми точками и затем находить абсциссу нужной точки.
Также существуют более сложные методы и формулы для аналитического нахождения абсциссы точки, например, линейная интерполяция или методы из математического анализа. Однако, для простых задач, формула расстояния между точками на плоскости является самым распространенным и удобным способом.
Важно помнить, что аналитическое вычисление абсциссы точки требует знания координат остальных точек на плоскости и применения соответствующих математических формул и методов.
Формула нахождения абсциссы
Пусть дана точка P, заданная координатами (x, y). Чтобы найти абсциссу x, нужно использовать формулу:
x = Px
где Px – x-координата заданной точки P.
Это простая формула, которая позволяет быстро определить абсциссу точки на координатной плоскости. Для более сложных случаев, когда точка задана в другой системе координат или требуется решить задачу нахождения абсциссы с помощью уравнений и дополнительных условий, могут применяться другие методы и техники.
Зная формулу нахождения абсциссы, можно легко и уверенно работать с координатами точек и решать различные задачи, связанные с геометрией, физикой, программированием и другими областями, где требуется работа с координатами.
Практические задачи и примеры

При решении задач по определению абсциссы точки большую роль играет геометрическое представление графика функции. Рассмотрим несколько практических задач и примеров, которые помогут лучше понять данную тему:
Задача 1:
Найдите абсциссу точки пересечения графика функции \(y = 2x - 3\) с осью OX.
Решение:
Для нахождения абсциссы точки пересечения с осью OX необходимо подставить \(y = 0\) в уравнение функции:
\(0 = 2x - 3\)
Приравняем \(0\) к \(2x - 3\):
\(2x - 3 = 0\)
Добавим \(3\) к обеим частям уравнения:
\(2x = 3\)
Разделим обе части уравнения на \(2\):
\(x = \dfrac{3}{2}\)
Таким образом, абсцисса точки пересечения графика функции с осью OX равна \(\dfrac{3}{2}\).
Задача 2:
Определите абсциссу точки, в которой график функции \(y = x^2 - 4x + 3\) пересекает ось OX.
Решение:
Для нахождения абсциссы точки пересечения с осью OX необходимо подставить \(y = 0\) в уравнение функции:
\(0 = x^2 - 4x + 3\)
Разложим данное уравнение на множители:
\(0 = (x - 1)(x - 3)\)
Так как произведение равно нулю, то один из множителей должен быть равен нулю:
\(x - 1 = 0\) или \(x - 3 = 0\)
Решим каждое уравнение относительно \(x\):
\(x = 1\) или \(x = 3\)
Таким образом, график функции \(y = x^2 - 4x + 3\) пересекает ось OX в точках с абсциссами \(1\) и \(3\).
Задача 3:
Найдите абсциссу точки пересечения графика функции \(y = \sqrt{3x}\) с осью OX.
Решение:
Для нахождения абсциссы точки пересечения с осью OX необходимо подставить \(y = 0\) в уравнение функции:
\(0 = \sqrt{3x}\)
Возведем обе части уравнения в квадрат:
\(0 = 3x\)
Так как \(3x = 0\), то \(x = 0\).
Таким образом, абсцисса точки пересечения графика функции с осью OX равна \(0\).
Упражнение:
Попробуйте решить еще несколько задач самостоятельно, чтобы закрепить полученные знания о способах определения абсциссы точки.
Абсцисса точки в пространстве
Для вычисления абсциссы точки в пространстве можно использовать следующую формулу:
- Если точка задана в прямоугольной системе координат, координаты которой обозначены как (x, y, z), то абсцисса точки равна x.
- Если точка задана в сферической системе координат, в которой координаты обозначены как (ρ, θ, φ), то абсцисса точки может быть вычислена следующим образом:
x = ρ * sin(θ) * cos(φ)
В данной формуле ρ представляет расстояние от начала координатной системы до точки, θ – угол между осью Z и линией, соединяющей точку с началом координат, а φ – угол между плоскостью XY и плоскостью, содержащей точку.
Зная абсциссу точки, можно определить ее положение относительно других объектов в пространстве и использовать эту информацию для решения различных задач, связанных с геометрией и физикой.