Четность функции – это одно из важнейших понятий в математике, которое позволяет анализировать и предсказывать поведение функции. В данной статье мы рассмотрим, как определить четность функции, основываясь на ее графике и аналитических свойствах.
Функция с косинусом – одна из классических функций, которая с успехом применяется в различных областях науки и инженерии. Косинус функция имеет свои особенности, включая периодичность и симметрию. С помощью этих особенностей и определений четности функций, мы можем легко сказать, является ли функция четной или нечетной.
Четность функции определяется симметрией ее графика относительно оси ординат (ось Y). Если для любого значения x входящего в область определения функции, выполняется тождество f(-x) = f(x), то функция является четной. Если же выполняется тождество f(-x) = -f(x) для любого значения x, то функция является нечетной. В ином случае функция является функцией смешанного типа и не обладает ни одним из свойств.
Определение четности функции с косинусом
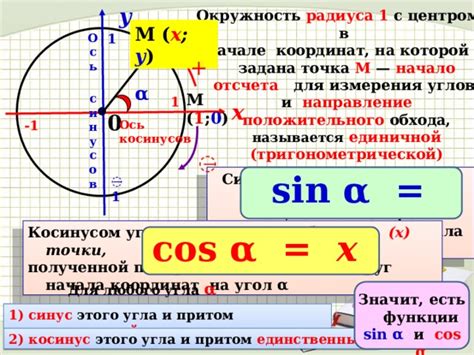
Чтобы узнать, является ли функция синуса четной или нечетной, необходимо проверить, выполняется ли следующее свойство:
f(x) = f(-x)
Если данное свойство выполняется, то функция является четной, иначе она является нечетной.
Если применить это свойство к косинусной функции, получим следующее:
cos(x) = cos(-x)
Таким образом, косинусная функция является четной, так как она симметрична относительно оси OY.
На графике косинусной функции это выражается тем, что график симметричен относительно оси OY и повторяется через каждые π радиан.
| Значение угла (x) | Значение косинуса (cos(x)) |
|---|---|
| 0 | 1 |
| π/2 | 0 |
| π | -1 |
| 3π/2 | 0 |
| 2π | 1 |
Таким образом, косинусная функция является четной и имеет период π.
Что такое четность функции?

В математике существует понятие четности функции, которое играет важную роль при изучении и анализе функций. Четность функции описывает, как симметрична функция относительно оси координат.
Функция считается четной, если она симметрична относительно вертикальной оси y, то есть f(x) = f(-x) для любого значения x. Это означает, что график функции симметричен относительно оси y.
Например, функция f(x) = cos(x) является четной функцией, так как cos(x) = cos(-x) для любого значения x. График функции cos(x) представляет собой симметричную волнообразную кривую относительно оси y, что подтверждает ее четность.
В то же время, функция считается нечетной, если она симметрична относительно начала координат (0,0), то есть f(x) = -f(-x) для любого значения x. Это означает, что график функции симметричен относительно начала координат.
Например, функция f(x) = sin(x) является нечетной функцией, так как sin(x) = -sin(-x) для любого значения x. График функции sin(x) также представляет собой волнообразную кривую, но симметричную относительно начала координат.
Как определить четность функции?

Для определения четности функции необходимо выполнить следующие шаги:
- Рассмотреть заданную функцию и проверить, является ли она периодической с периодом T.
- Если функция периодическая, то проверить, выполняется ли свойство f(x) = f(x + T/2) для всех x, где T/2 - половина периода функции.
- Если выполняется свойство f(x) = f(x + T/2), то функция считается четной.
- Если свойство f(x) = f(x + T/2) не выполняется, то необходимо проверить, выполняется ли свойство f(x) = -f(x + T/2) для всех x.
- Если выполняется свойство f(x) = -f(x + T/2), то функция считается нечетной.
- Если ни одно из указанных свойств не выполняется, то функцию нельзя отнести ни к четным, ни к нечетным.
Таким образом, четность функции определяется с помощью анализа ее периодичности и выполнения соответствующих свойств при сдвиге аргумента.
Как определить четность функции с косинусом?

Определение четности функции с косинусом основано на анализе ее графика и свойств косинуса. Для определения четности функции, нужно рассмотреть значения функции для положительных и отрицательных аргументов.
Косинусная функция f(x) = cos(x) имеет следующие свойства:
| Знак аргумента (x) | Значение функции (f(x)) |
|---|---|
| Положительный (x > 0) | Положительное или нулевое (f(x) ≥ 0) |
| Отрицательный (x < 0) | Положительное или нулевое (f(x) ≥ 0) |
Из этой таблицы видно, что значение косинусной функции f(x) всегда неотрицательно, независимо от знака аргумента x. То есть, график функции с косинусом симметричен относительно оси ординат. Это означает, что косинусная функция является четной функцией.
Таким образом, для любого значения аргумента x, значение функции f(x) = cos(x) будет равно f(-x) = cos(-x), что позволяет заключить, что косинусная функция четна.
Подробное руководство по определению четности функции с косинусом

Для начала, отобразим значения косинуса на графике для различных значений угла:
| Угол (в радианах) | Косинус угла |
|---|---|
| 0 | 1 |
| π/6 | √3/2 |
| π/4 | √2/2 |
| π/3 | 1/2 |
| π/2 | 0 |
Из таблицы видно, что косинус положительный для углов от 0 до π/2. Таким образом, функция косинуса является четной на этом интервале.
Для проверки четности функции с косинусом можно использовать свойство замены аргумента:
Пусть f(x) - функция косинуса. Если f(x) равно f(-x) для всех x в интервале от 0 до π/2, то функция является четной.
Например, рассмотрим функцию f(x) = cos(x). Подставим вместо x значение -x:
f(-x) = cos(-x) = cos(x)
Таким образом, функция f(x) = cos(x) является четной.
Следует отметить, что функция косинуса не является четной на всей числовой прямой. На интервале от π/2 до π косинус является отрицательным, поэтому функция косинуса не является четной на данном интервале.
Примеры определения четности функции с косинусом

В данном разделе мы рассмотрим несколько примеров, позволяющих определить четность функции с косинусом.
- Пример 1:
- Пример 2:
- Пример 3:
Рассмотрим функцию f(x) = cos(x). Чтобы определить ее четность, необходимо проверить выполнение следующего свойства: для любого значения аргумента x должно выполняться условие f(-x) = f(x). В данном случае, заменив x на -x в функции, получим cos(-x) = cos(x). Таким образом, функция f(x) является четной.
Рассмотрим функцию g(x) = cos(2x). Для определения ее четности, можно воспользоваться аналогичным свойством: g(-x) = g(x). В данном случае, заменив x на -x в функции, получим cos(-2x) = cos(2x). Таким образом, функция g(x) также является четной.
Рассмотрим функцию h(x) = cos(x) + sin(x). Чтобы определить ее четность, нужно проверить выполнение условия h(-x) = -h(x). Заменив x на -x в функции, получим cos(-x) + sin(-x) = -(cos(x) + sin(x)). Таким образом, функция h(x) является нечетной.
Таким образом, определить четность функции с косинусом можно, заменяя переменную на противоположное значение и проверяя равенство функции с самой собой или с отрицанием функции.
Ресурсы
При определении четности функции с косинусом полезно использовать следующие ресурсы:
1. Математические книги:
Изучение математических книг поможет вам углубить свои знания о косинусе и его свойствах. Рекомендуемые книги включают "Математический анализ" А.М. Лысицына и "Функциональный анализ" В.А. Садовничего.
2. Онлайн ресурсы:
Существует множество веб-сайтов и приложений, которые предлагают инструменты для анализа функций с косинусом. Примеры таких ресурсов включают Wolfram Alpha и Desmos.
3.Учебные видео:
Интерактивные учебные видео на платформах, таких как YouTube или Khan Academy, могут быть полезными для получения визуального объяснения того, как определить четность функции с косинусом.
Учет этих ресурсов поможет вам более глубоко понять тему и применить полученные знания к решению конкретных задач.