Число степеней свободы является важным понятием во многих областях науки и статистики. Оно используется для определения степени вариации данных и оценки статистической значимости результатов исследований.
Число степеней свободы обозначается как df и представляет собой количество независимых переменных, которые могут изменяться в рамках системы или эксперимента. Например, в эксперименте с двумя группами, число степеней свободы будет равно одному, так как есть только одна независимая переменная - фактор группы.
Для определения числа степеней свободы необходимо учитывать количество категорий в переменных, количество групп, объем выборки и другие факторы. В общем случае, для вычисления числа степеней свободы используются различные статистические методы, такие как анализ дисперсии (ANOVA), t-тесты и хи-квадрат тесты.
Что такое число степеней свободы и как его найти?
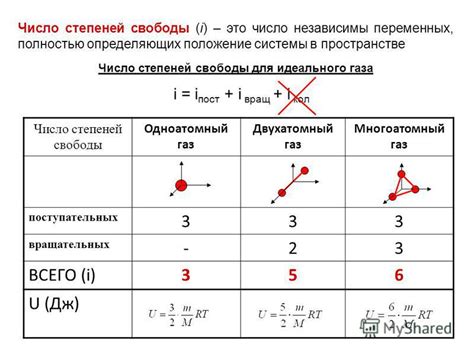
Для каждого типа статистического теста или модели количество степеней свободы может быть разным. В основе вычисления ЧСС лежит понятие ограничений, которые налагаются на переменные при проведении анализа. Чем больше ограничений, тем меньше степеней свободы.
На практике число степеней свободы может быть найдено различными способами в зависимости от типа задачи:
- Для t-критерия Стьюдента число степеней свободы равно разности между количеством наблюдений и количеством оцениваемых параметров.
- Для анализа дисперсии (ANOVA) число степеней свободы для факторов определяется как количество групп (уровней фактора) минус 1.
- Для анализа ковариации (ANCOVA) число степеней свободы рассчитывается как количество групп (уровней фактора) минус 1, минус количество оцениваемых параметров.
Определение понятия "число степеней свободы"
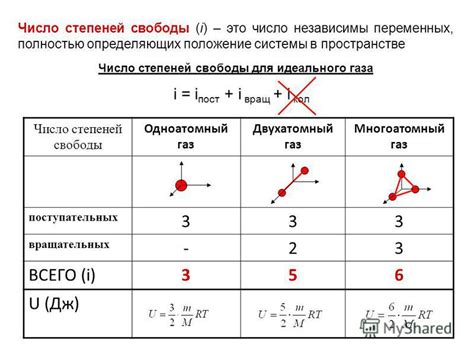
В случае статистики, число степеней свободы определяет количество независимых наблюдений или исходных данных, которые могут быть использованы для анализа. Например, если у нас есть выборка из 100 человек, то число степеней свободы будет равно 99, так как одно наблюдение может быть связано с другими.
В науке о материалах число степеней свободы может описывать количество способов, которыми атомы или молекулы могут двигаться или колебаться. Например, в трехмерном пространстве каждая атомная или молекулярная система может иметь до 3n степеней свободы, где n - число атомов или молекул.
Формула расчета числа степеней свободы
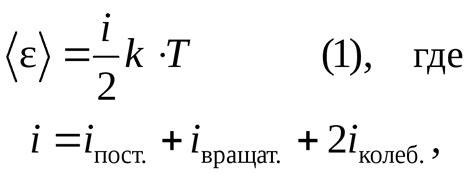
Рассмотрим некоторые примеры расчета числа степеней свободы:
Одновыборочный t-тест - используется для сравнения средних значений выборки с некоторым эталонным значением. Для расчета числа степеней свободы используется формула df = n - 1, где n - это размер выборки.
Двухвыборочный t-тест - используется для сравнения средних значений двух независимых выборок. Число степеней свободы рассчитывается по формуле df = n1 + n2 - 2, где n1 и n2 - размеры двух выборок.
Анализ дисперсии (ANOVA) - используется для сравнения средних значений более чем двух независимых выборок. Число степеней свободы в этом случае рассчитывается по формуле df = k - 1, где k - количество групп или уровней фактора.
Хи-квадрат (χ²) тест независимости - используется для проверки связи между двумя категориальными переменными. Число степеней свободы в этом случае рассчитывается по формуле df = (r - 1) * (c - 1), где r и c - количество строк и столбцов таблицы сопряженности.
Формулы расчета числа степеней свободы могут различаться в зависимости от типа статистического теста. Важно правильно определить число степеней свободы, чтобы получить достоверные результаты анализа данных.
Примеры расчета числа степеней свободы
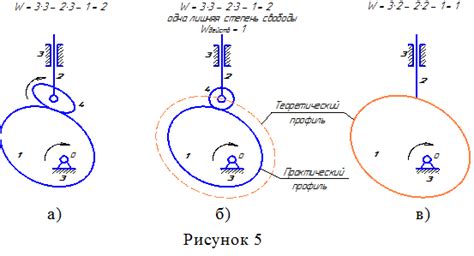
Рассмотрим несколько примеров расчета числа степеней свободы в различных задачах:
Пример 1:
Пусть у нас есть выборка из 100 наблюдений. Мы хотим определить количество степеней свободы для проверки значимости различия между двумя средними.
Число степеней свободы в данной задаче будет равно (число наблюдений - 1) для каждой выборки, то есть (100-1) = 99.
Пример 2:
Предположим, мы проводим анализ ковариации для двух факторов: возраст и доход. У нас есть 3 возрастные группы (18-30, 31-50, 51-70) и 4 группы дохода (низкий, средний, высокий, очень высокий). Количество наблюдений в каждой группе следующее: 20, 30, 25 для возраста и 15, 20, 10, 25 для дохода.
Число степеней свободы в данной задаче будет равно (число групп - 1) для каждого фактора, то есть (3-1) = 2 для возраста и (4-1) = 3 для дохода.
Пример 3:
Представим, что у нас есть таблица сопряженности, которая показывает количество студентов, получивших разные оценки по предмету A и предмету B. Количество степеней свободы в такой задаче будет зависеть от размеров таблицы.
Пусть размеры таблицы следующие: 2 строки (оценки по предмету A) и 3 столбца (оценки по предмету B). Число степеней свободы будет равно (число строк - 1) * (число столбцов - 1), то есть (2-1) * (3-1) = 1 * 2 = 2.
Объяснение принципа определения числа степеней свободы
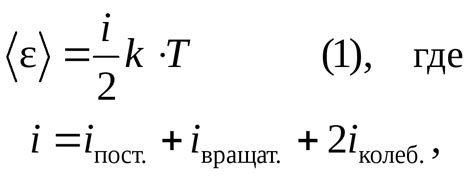
Чтобы определить число степеней свободы в системе, нужно учитывать количество независимых переменных, которые могут меняться. Например, если у нас есть система из трех шаров, расположенных на плоскости, то каждый шар может иметь две степени свободы: движение по горизонтали и движение по вертикали. Таким образом, общее число степеней свободы в этой системе будет равно 3 шара * 2 степени свободы на шар = 6.
В другом примере, когда мы имеем систему с пружиной, число степеней свободы будет зависеть от числа связей. Если пружина закреплена только с одной стороны, то у нее будет одна степень свободы (длина пружины). А если пружина закреплена с обоих концов, то у нее будет две степени свободы (длина пружины и угол поворота). Таким образом, число степеней свободы в системе с пружиной будет зависеть от числа связей и их типа.
Зная число степеней свободы в системе, мы можем определить ее характеристики и поведение, такие как энергия, колебания, и распределение по фазовому пространству. Поэтому понимание и определение числа степеней свободы важно для анализа и моделирования различных систем и явлений.
Значение числа степеней свободы в статистике
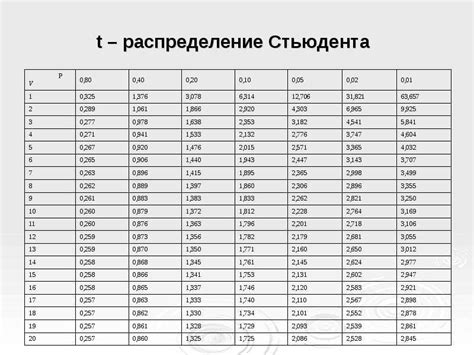
Таблица ниже показывает значения числа степеней свободы для различных статистических тестов:
| Тест | Число степеней свободы |
|---|---|
| t-тест | число наблюдений - 1 |
| ANOVA | число групп - 1 |
| Хи-квадрат тест | (число строк - 1) * (число столбцов - 1) |
Важно помнить, что число степеней свободы может быть случаем, где это количество человек, но в широком смысле число степеней свободы является характеристикой модели на основании данных выборки.
Применение числа степеней свободы в научных исследованиях

Число степеней свободы (называемое также df) играет важную роль в научных исследованиях. Оно представляет собой меру количества независимой информации, которая может быть использована для проверки статистической гипотезы и получения статистически значимых результатов.
Число степеней свободы определяется в зависимости от типа статистического теста, используемого в исследовании. Например, в случае t-теста, df будет равно (n-1), где n представляет собой размер выборки. Это означает, что для того, чтобы использовать t-тест и получить статистически значимые результаты, необходимо иметь достаточно большую выборку данных.
В других исследованиях, например, анализе дисперсии (ANOVA), число степеней свободы будет определяться как разница между общим числом наблюдений и числом ограничений, налагаемых на данные. Эти ограничения могут быть вызваны различными факторами или влиянием обработки данных.